Zipf's law
From Wikipedia, the free encyclopedia
Probability mass function Zipf PMF for N = 10 on a log-log scale. The horizontal axis is the index k . (Note that the function is only defined at integer values of k. The connecting lines do not indicate continuity.) |
|
Cumulative distribution function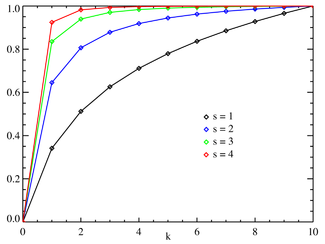 Zipf CMF for N = 10. The horizontal axis is the index k . (Note that the function is only defined at integer values of k. The connecting lines do not indicate continuity.) |
|
| Parameters | 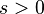 (real) (real)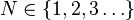 (integer) (integer) |
|---|---|
| Support | 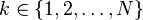 |
| Probability mass function (pmf) | 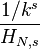 |
| Cumulative distribution function (cdf) | 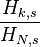 |
| Mean | 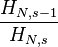 |
| Median | |
| Mode |  |
| Variance | |
| Skewness | |
| Excess kurtosis | |
| Entropy |  |
| Moment-generating function (mgf) |  |
| Characteristic function |  |
Zipf's law, an empirical law formulated using mathematical statistics, refers to the fact that many types of data studied in the physical and social sciences can be approximated with a Zipfian distribution, one of a family of related discrete power law probability distributions. The law is named after the linguist George Kingsley Zipf (pronounced /zɪf/) who first proposed it (Zipf 1935, 1949), though J.B. Estoup appears to have noticed the regularity before Zipf.[1].
Contents |
[edit] Motivation
Zipf's law states that given some corpus of natural language utterances, the frequency of any word is inversely proportional to its rank in the frequency table. Thus the most frequent word will occur approximately twice as often as the second most frequent word, which occurs twice as often as the fourth most frequent word, etc. For example, in the Brown Corpus "the" is the most frequently occurring word, and by itself accounts for nearly 7% of all word occurrences (69,971 out of slightly over 1 million). True to Zipf's Law, the second-place word "of" accounts for slightly over 3.5% of words (36,411 occurrences), followed by "and" (28,852). Only 135 vocabulary items are needed to account for half the Brown Corpus.
[edit] Theoretical review
Zipf's law is most easily observed by plotting the data on a log-log graph, with the axes being log(rank order) and log(frequency). For example, "the" as described above would appear at x = log(1), y = log(69971). The data conform to Zipf's law to the extent that the plotted points appear to fall along a single line segment.
Formally, let:
- N be the number of elements;
- k be their rank;
- s be the value of the exponent characterizing the distribution.
Zipf's law then predicts that out of a population of N elements, the frequency of elements of rank k, f(k;s,N), is:
In the example of the frequency of words in the English language, N is the number of words in the English language and, if we use the classic version of Zipf's law, the exponent s is 1. f(k; s,N) will then be the fraction of the time the kth most common word occurs.
It is easily seen that the distribution is normalized, i.e., the predicted frequencies sum to 1:
The law may also be written:
where HN,s is the Nth generalized harmonic number.
The simplest case of Zipf's law is a "1/f function". Given a set of Zipfian distributed frequencies, sorted from most common to least common, the second most common frequency will occur ½ as often as the first. The third most common frequency will occur 1/3 as often as the first. The nth most common frequency will occur 1/n as often as the first. However, this cannot hold exactly, because items must occur an integer number of times: there cannot be 2.5 occurrences of a word. Nevertheless, over fairly wide ranges, and to a fairly good approximation, many natural phenomena obey Zipf's law.
Mathematically, it is impossible for the classic version of Zipf's law to hold exactly if there are infinitely many words in a language, since the sum of all relative frequencies in the denominator above is equal to the harmonic series and therefore:
In English, the frequencies of the approximately 1000 most-frequently-used words are approximately proportional to 1/ns where s is just slightly more than one.[citation needed]
As long as the exponent s exceeds 1, it is possible for such a law to hold with infinitely many words, since if s > 1 then
where ζ is Riemann's zeta function.
[edit] Theoretical issues
Just why data conform to Zipfian distributions can be a matter of some controversy. That Zipfian distributions arise in randomly-generated texts suggests that in linguistic contexts, the law is a statistical artifact.[2] That is, one starts with an alphabet of N letters, one of which is a blank space, and thus acts as a word separator. By picking letters randomly, with a uniform distribution, one generates a random string; the string will consist of "words" of various lengths. After ranking these words, and plotting their frequency, one obtains precisely Zipf's law. Thus, Zipf's law does not seem to shed any light on the linguistic structure of language, but is rather an artifact of using letters to spell words.
[edit] Related laws
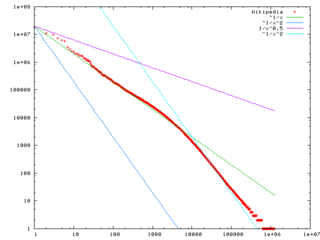
Zipf's law now refers more generally to frequency distributions of "rank data," in which the relative frequency of the nth-ranked item is given by the Zeta distribution, 1/(nsζ(s)), where the parameter s > 1 indexes the members of this family of probability distributions. Indeed, Zipf's law is sometimes synonymous with "zeta distribution," since probability distributions are sometimes called "laws". This distribution is sometimes called the Zipfian or Yule distribution.
A generalization of Zipf's law is the Zipf–Mandelbrot law, proposed by Benoît Mandelbrot, whose frequencies are:
The "constant" is the reciprocal of the Hurwitz zeta function evaluated at s.
Zipfian distributions can be obtained from Pareto distributions by an exchange of variables.[3]
The tail frequencies of the Yule–Simon distribution are approximately
for any choice of ρ > 0.
If the natural log of some data are normally distributed, the data follow the log-normal distribution. This distribution is useful when random influences have an effect that is multiplicative rather than additive.
In the parabolic fractal distribution, the logarithm of the frequency is a quadratic polynomial of the logarithm of the rank. This can markedly improve the fit over a simple power-law relationship.[3] Like fractal dimension, it is possible to calculate Zipf dimension, which is a useful parameter in the analysis of texts.[4]
It has been argued that Benford's law is a special case of Zipf's law.[3]
[edit] See also
[edit] References
- ^ Christopher D. Manning, Hinrich Schütze Foundations of Statistical Natural Language Processing, MIT Press (1999), ISBN 978-0262133609, p. 24
- ^ Wentian Li (1992). "Random Texts Exhibit Zipf's-Law-Like Word Frequency Distribution". IEEE Transactions on Information Theory 38 (6): 1842–1845. doi:. http://www.nslij-genetics.org/wli/pub/ieee92_pre.pdf.
- ^ a b c Johan Gerard van der Galien (2003-11-08). "Factorial randomness: the Laws of Benford and Zipf with respect to the first digit distribution of the factor sequence from the natural numbers". http://home.zonnet.nl/galien8/factor/factor.html.
- ^ Ali Eftekhari (2006) Fractal geometry of texts. Journal of Quantitative Linguistic 13(2-3): 177 – 193.
[edit] Further reading
Primary:
- George K. Zipf (1949) Human Behavior and the Principle of Least-Effort. Addison-Wesley.
- -------- (1935) The Psychobiology of Language. Houghton-Mifflin. (see citations at http://citeseer.ist.psu.edu/context/64879/0 )
Secondary:
- Gelbukh, Alexander, and Sidorov, Grigori (2001) "Zipf and Heaps Laws’ Coefficients Depend on Language". Proc. CICLing-2001, Conference on Intelligent Text Processing and Computational Linguistics, February 18–24, 2001, Mexico City. Lecture Notes in Computer Science N 2004, ISSN 0302-9743, ISBN 3-540-41687-0, Springer-Verlag: 332–335.
- Damián H. Zanette (2006) "Zipf's law and the creation of musical context," Musicae Scientiae 10: 3-18.
- Kali R. (2003) "The city as a giant component: a random graph approach to Zipf's law," Applied Economics Letters 10: 717-720(4)
- Gabaix, Xavier (August 1999). "Zipf's Law for Cities: An Explanation". Quarterly Journal of Economics 114 (3): 739–67. doi:. ISSN 0033-5533. http://pages.stern.nyu.edu/~xgabaix/papers/zipf.pdf.
[edit] External links
- Comprehensive bibliography of Zipf's law
- Zipf, Power-laws, and Pareto - a ranking tutorial
- Seeing Around Corners (Artificial societies turn up Zipf's law)
- PlanetMath article on Zipf's law
- Distributions de type “fractal parabolique” dans la Nature (French, with English summary)
- An analysis of income distribution
- Zipf List of French words
- Zipf list English words (extracted from www.jane16.com engine)
- Citations and the Zipf-Mandelbrot's law
- Zipf's Law for U.S. Cities by Fiona Maclachlan, Wolfram Demonstrations Project.
- Eric W. Weisstein, Zipf's Law at MathWorld.





![f(k;N,q,s)=[\mbox{constant}]/(k+q)^s.\,](http://upload.wikimedia.org/math/c/8/0/c80de7116cb6a160f4bca6a4dee5094a.png)
![f(k;\rho) \approx [\mbox{constant}]/k^{\rho+1}](http://upload.wikimedia.org/math/f/f/1/ff1f9b6dd75c89477e5e5f13cda6d9a3.png)

