Formal language

From Wikipedia, the free encyclopedia

Jump to: navigation, search
This article is about a technical term in mathematics and computer science. For related studies about natural languages, see grammar framework. For formal language as a mode of speech, see Register (linguistics).

A formal language is a set of words, i.e. finite strings of letters, or symbols. The inventory from which these letters are taken is called the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar. Formal languages are a purely syntactical notion, so there is not necessarily any meaning associated with them. To distinguish the words that belong to a language from arbitrary words over its alphabet, the former are sometimes called well-formed words (or, in their application in logic, well-formed formulas).

Formal languages are studied in the fields of logic, computer science and linguistics. Their most important practical application is for the precise definition of syntactically correct programs for a programming language. The branch of mathematics and computer science that is concerned only with the purely syntactical aspects of such languages, i.e. their internal structural patterns, is known as formal language theory.

Although it is not formally part of the language, the words of a formal language often have a semantic dimension as well. In practice this is always tied very closely to the structure of the language, and a formal grammar (a set of formation rules that recursively describes the language) can help to deal with the meaning of (well-formed) words. Well-known examples for this are "Tarski's definition of truth" in terms of a T-schema for first-order logic, and compiler generators like lex and yacc.

Contents

[edit] Words over an alphabet

An alphabet, in the context of formal languages can be any set, although it often makes sense to use an alphabet in the usual sense of the word, or more generally a character set such as ASCII. Alphabets can also be infinite; e.g. first-order logic is often expressed using an alphabet which, besides symbols such as ∧, ¬, ∀ and parentheses, contains infinitely many elements x0, x1, x2, … that play the role of variables. The elements of an alphabet are called its letters.

A word over an alphabet can be any finite sequence, or string, of letters. The set of all words over an alphabet Σ is usually denoted by Σ* (using the Kleene star). For any alphabet there is only one word of length 0, the empty word, which is often denoted by e, ε or λ. By concatenation one can combine two words to form a new word, whose length is the sum of the lengths of the original words. The result of concatenating a word with the empty word is the original word.

In some applications, especially in logic, the alphabet is also known as the vocabulary and words are known as formulas or sentences; this breaks the letter/word metaphor and replaces it by a word/sentence metaphor.

[edit] Definition

A formal language L over an alphabet Σ is just a subset of Σ*, that is, a set of words over that alphabet.

In computer science and mathematics, which do not deal with natural languages, the adjective "formal" is usually omitted as redundant.

While formal language theory usually concerns itself with formal languages that are described by some syntactical rules, the actual definition of the concept "formal language" is only as above: a (possibly infinite) set of finite-length strings, no more nor less. In practice, there are many languages that can be described by rules, such as regular languages or context-free languages. The notion of a formal grammar may be closer to the intuitive concept of a "language," one described by syntactic rules. By an abuse of the definition, a particular formal language is often thought of as being equipped with a formal grammar that describes it.

[edit] Examples

The following rules describe a formal language L over the alphabet Σ = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +, =}:

  • Every nonempty string that does not contain + or = and does not start with 0 is in L.
  • The string 0 is in L.
  • A string containing = is in L if and only if there is exactly one =, and it separates two valid strings in L.
  • A string containing + is in L if and only if every + in the string separates two valid strings in L.
  • No string is in L other than those implied by the previous rules.

Under these rules, the string "23+4=555" is in L, but the string "=234=+" is not. This formal language expresses natural numbers, well-formed addition statements, and well-formed addition equalities, but it expresses only what they look like (their syntax), not what they mean (semantics). For instance, nowhere in these rules is there any indication that 0 means the number zero, or that + means addition.

For finite languages one can simply enumerate all well-formed words. For example, we can describe a language L as just L = {"a", "b", "ab", "cba"}.

However, even over a finite (non-empty) alphabet such as Σ = {a, b} there are infinitely many words: "a", "abb", "ababba", "aaababbbbaab", …. Therefore formal languages are typically infinite, and describing an infinite formal language is not as simple as writing L = {"a", "b", "ab", "cba"}. Here are some examples of formal languages:

  • L = Σ*, the set of all words over Σ;
  • L = {a}* = {an}, where n ranges over the natural numbers and an means "a" repeated n times (this is the set of words consisting only of the symbol "a");
  • the set of syntactically correct programs in a given programming language (the syntax of which is usually defined by a context-free grammar;
  • the set of inputs upon which a certain Turing machine halts; or
  • the set of maximal strings of alphanumeric ASCII characters on this line, (i.e., the set {"the", "set", "of", "maximal", "strings", "alphanumeric", "ASCII", "characters", "on", "this", "line", "i", "e"}).

[edit] Language-specification formalisms

Formal language theory rarely concerns itself with particular languages (except as examples), but is mainly concerned with the study of various types of formalisms to describe languages. For instance, a language can be given as

Typical questions asked about such formalisms include:

  • What is their expressive power? (Can formalism X describe every language that formalism Y can describe? Can it describe other languages?)
  • What is their recognizability? (How difficult is it to decide whether a given word belongs to a language described by formalism X?)
  • What is their comparability? (How difficult is it to decide whether two languages, one described in formalism X and one in formalism Y, or in X again, are actually the same language?).

Surprisingly often, the answer to these decision problems is "it cannot be done at all", or "it is extremely expensive" (with a precise characterization of how expensive exactly). Therefore, formal language theory is a major application area of computability theory and complexity theory.

[edit] Operations on languages

Certain operations on languages are common. This includes the standard set operations, such as union, intersection, and complement. Another class of operation is the element-wise application of string operations.

Examples: suppose L1 and L2 are languages over some common alphabet.

  • The concatenation L1L2 consists of all strings of the form vw where v is a string from L1 and w is a string from L2.
  • The intersection L1 ∩ L2 of L1 and L2 consists of all strings which are contained in both languages
  • The complement ¬L of a language with respect to a given alphabet consists of all strings over the alphabet that are not in the language.
  • The Kleene star: the language consisting of all words that are concatenations of 0 or more words in the original language;
  • Reversal:
    • Let e be the empty word, then eR = e, and
    • for each non-empty word w = x1…xn over some alphabet, let wR = xn…x1,
    • then for a formal language L, LR = {wR | w ∈ L}.
  • String homomorphism.

Such string operations are used to investigate closure properties of classes of languages. A class of languages is closed under a particular operation when the operation, applied to languages in the class, always produces a language in the same class again. For instance, the context-free languages are known to be closed under union, concatenation, and intersection with regular languages, but not closed under intersection or complement.

Closure properties of language families (L1 Op L2 where both L1 and L2 are in the language family given by the column). After Hopcroft and Ullman.
Operation regular DCFL CFL CSL recursive r.e.
Union 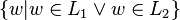\{w | w \in L_1 \lor w \in L_2\} Yes No Yes Yes Yes Yes
Intersection 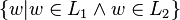\{w | w \in L_1 \land w \in L_2\} Yes No No Yes Yes Yes
Complement \{w | w \not\in L_1\} Yes Yes No Yes Yes No
Concatenation L_1\cdot L_2 = \{w\cdot z | w \in L_1 \land z \in L_2\} Yes No Yes Yes Yes Yes
Kleene star 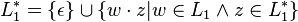L_1^{*} = \{\epsilon\} \cup \{w \cdot z | w \in L_1 \land z \in L_1^{*}\} Yes No Yes Yes Yes Yes
Homomorphism Yes No Yes Yes No Yes
Substitution Yes No Yes Yes No Yes
Inverse Homomorphism Yes Yes Yes Yes Yes Yes
Reverse 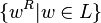\{w^R | w \in L\} Yes No Yes Yes Yes Yes

[edit] References

  • A. G. Hamilton, Logic for Mathematicians, Cambridge University Press, 1978, ISBN 0 521 21838 1.
  • Seymour Ginsburg, Algebraic and automata theoretic properties of formal languages, North-Holland, 1975, ISBN 0 7204 2506 9.
  • Michael A. Harrison, Introduction to Formal Language Theory, Addison-Wesley, 1978.
  • John E. Hopcroft and Jeffrey D. Ullman, Introduction to Automata Theory, Languages and Computation, Addison-Wesley Publishing, Reading Massachusetts, 1979. ISBN 0-201-029880-X.
  • Grzegorz Rozenberg, Arto Salomaa, Handbook of Formal Languages: Volume I-III, Springer, 1997, ISBN 3 540 61486 9.
  • Patrick Suppes, Introduction to Logic, D. Van Nostrand, 1957, ISBN 0 442 08072 7.

[edit] See also

[edit] External links

Retrieved from "http://en.wikipedia.org/wiki/Formal_language"
Personal tools