Saul Kripke
From Wikipedia, the free encyclopedia
| Western Philosophy 20th-century philosophy |
|
 |
|
| Full name | Saul Kripke |
|---|---|
| School/tradition | Analytic |
| Main interests | Logic (particularly modal) Philosophy of language Metaphysics Set Theory Epistemology Philosophy of Mind History of Analytic Philosophy |
| Notable ideas | Causal theory of reference Kripkenstein admissible ordinal rigid designator Kripke semantics |
|
Influenced by
|
|
|
Influenced
|
|
Saul Aaron Kripke (born on November 13, 1940 in Bay Shore, New York) is an American philosopher and logician, now emeritus from Princeton. He teaches as distinguished professor of philosophy at CUNY Graduate Center. Since the 1960s Kripke has been a central figure in a number of fields related to logic, philosophy of language, metaphysics, epistemology, and set theory. Much of his work remains unpublished or exists only as tape-recordings and privately circulated manuscripts (see "Unpublished Manuscripts and Online Lectures" below). Kripke was the recipient of the 2001 Schock Prize in Logic and Philosophy. He has received honorary degrees from the University of Nebraska, Omaha (1977), Johns Hopkins University (1997), University of Haifa, Israel (1998), and the University of Pennsylvania (2005). He is a member of the American Philosophical Society. Kripke is also an elected Fellow of the American Academy of Arts and Sciences and a Corresponding Fellow of the British Academy.
[edit] Biography
Saul Kripke is the eldest of three children born to Dorothy K. Kripke and Rabbi Myer Kripke. His father was the leader of Beth El Synagogue, the only Conservative congregation in Omaha, Nebraska. His mother wrote Jewish educational children's books. Saul and his two sisters, Madeline and Netta, attended Dundee Grade School in Omaha and Omaha Central High School. He wrote his first essay at the age of sixteen on the semantics of modal logics. After graduating from high school in 1958, Kripke attended Harvard University and graduated summa cum laude obtaining a bachelor's degree in mathematics. He has no other non-honorary degrees. During his sophomore year at Harvard, Kripke taught a graduate-level logic course at nearby MIT. Upon graduation (1962) he received a Fulbright Fellowship. In 1963 he was appointed to the Society of Fellows. For some years he taught at Harvard, moved to Rockefeller University in New York City in 1967, then to Princeton University full-time in 1977. In 1976 Kripke married (and in the '90s divorced) the philosopher Margaret Gilbert. In 1988 he received Princeton's Behrman Award for distinguished achievement in the humanities. In 2002 Kripke started teaching at the CUNY Graduate Center in midtown Manhattan, and was appointed a distinguished professor of philosophy there in 2003.
[edit] Work
Kripke is best known for four contributions to philosophy:
- Kripke semantics for modal and related logics, published in several essays beginning while he was still in his teens.
- His 1970 Princeton lectures Naming and Necessity (published in 1972 and 1980), that significantly restructured the philosophy of language and, as some have put it, "made metaphysics respectable again"[1].
- His interpretation of the philosophy of Wittgenstein.
- His theory of truth.
He has also contributed to set-theory (see admissible ordinal and Kripke-Platek set theory)
[edit] Modal logic
Two of Kripke's earlier works ("A Completeness Theorem in Modal Logic" and "Semantical Considerations on Modal Logic"), the former written while he was still a teenager, were on the subject of modal logic. The most familiar logics in the modal family are constructed from a weak logic called K, named after Kripke for his contributions to modal logic. Kripke introduced the now-standard Kripke semantics (also known as relational semantics or frame semantics) for modal logics. Kripke semantics is a formal semantics for non-classical logic systems. It was first made for modal logics, and later adapted to intuitionistic logic and other non-classical systems. The discovery of Kripke semantics was a breakthrough in the making of non-classical logics, because the model theory of such logics was nonexistent before Kripke.
A Kripke frame or modal frame is a pair  , where W is a non-empty set, and R is a binary relation on W. Elements of W are called nodes or worlds, and R is known as the accessibility relation.
, where W is a non-empty set, and R is a binary relation on W. Elements of W are called nodes or worlds, and R is known as the accessibility relation.
A Kripke model is a triple  , where
, where  is a Kripke frame, and
is a Kripke frame, and  is a relation between nodes of W and modal formulas, such that:
is a relation between nodes of W and modal formulas, such that:
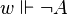 if and only if
if and only if  ,
,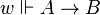 if and only if
if and only if  or
or 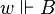 ,
,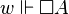 if and only if
if and only if  .
.
We read  as “w satisfies A”, “A is satisfied in w”, or “w forces A”. The relation
as “w satisfies A”, “A is satisfied in w”, or “w forces A”. The relation  is called the satisfaction relation, evaluation, or forcing relation. The satisfaction relation is uniquely determined by its value on propositional variables.
is called the satisfaction relation, evaluation, or forcing relation. The satisfaction relation is uniquely determined by its value on propositional variables.
A formula A is valid in:
- a model
 , if
, if  for all w ∈ W,
for all w ∈ W, - a frame
 , if it is valid in
, if it is valid in  for all possible choices of
for all possible choices of  ,
, - a class C of frames or models, if it is valid in every member of C.
We define Thm(C) to be the set of all formulas that are valid in C. Conversely, if X is a set of formulas, let Mod(X) be the class of all frames which validate every formula from X.
A modal logic (i.e., a set of formulas) L is sound with respect to a class of frames C, if L ⊆ Thm(C). L is complete wrt C if L ⊇ Thm(C).
Semantics is useful for investigating a logic (i.e. a derivation system) only if the semantical entailment relation reflects its syntactical counterpart, the consequence relation (derivability). It is vital to know which modal logics are sound and complete with respect to a class of Kripke frames, and for them, to determine which class it is.
For any class C of Kripke frames, Thm(C) is a normal modal logic (in particular, theorems of the minimal normal modal logic, K, are valid in every Kripke model). However, the converse does not hold in general. There are Kripke incomplete normal modal logics, which is not a problem, because most of the modal systems studied are complete of classes of frames described by simple conditions.
A normal modal logic L corresponds to a class of frames C, if C = Mod(L). In other words, C is the largest class of frames such that L is sound wrt C. It follows that L is Kripke complete if and only if it is complete of its corresponding class.
Consider the schema T :  . T is valid in any reflexive frame
. T is valid in any reflexive frame  : if
: if 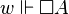 , then
, then  since w R w. On the other hand, a frame which validates T has to be reflexive: fix w ∈ W, and define satisfaction of a propositional variable p as follows:
since w R w. On the other hand, a frame which validates T has to be reflexive: fix w ∈ W, and define satisfaction of a propositional variable p as follows: 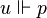 if and only if w R u. Then
if and only if w R u. Then  , thus
, thus  by T, which means w R w using the definition of
by T, which means w R w using the definition of  . T corresponds to the class of reflexive Kripke frames.
. T corresponds to the class of reflexive Kripke frames.
It is often much easier to characterize the corresponding class of L than to prove its completeness, thus correspondence serves as a guide to completeness proofs. Correspondence is also used to show incompleteness of modal logics: suppose L1 ⊆ L2 are normal modal logics that correspond to the same class of frames, but L1 does not prove all theorems of L2. Then L1 is Kripke incomplete. For example, the schema  generates an incomplete logic, as it corresponds to the same class of frames as GL (viz. transitive and converse well-founded frames), but does not prove the GL-tautology
generates an incomplete logic, as it corresponds to the same class of frames as GL (viz. transitive and converse well-founded frames), but does not prove the GL-tautology 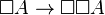 .
.
For any normal modal logic L, a Kripke model (called the canonical model) can be constructed, which validates precisely the theorems of L, by an adaptation of the standard technique of using maximal consistent sets as models. Canonical Kripke models play a role similar to the Lindenbaum – Tarski algebra construction in algebraic semantics.
A set of formulas is L-consistent if no contradiction can be derived from them using the axioms of L, and Modus Ponens. A maximal L-consistent set (an L-MCS for short) is an L-consistent set which has no proper L-consistent superset.
The canonical model of L is a Kripke model  , where W is the set of all L-MCS, and the relations R and
, where W is the set of all L-MCS, and the relations R and  are as follows:
are as follows:
 if and only if for every formula A, if
if and only if for every formula A, if  then
then 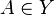 ,
, if and only if
if and only if  .
.
The canonical model is a model of L, as every L-MCS contains all theorems of L. By Zorn's lemma, each L-consistent set is contained in an L-MCS, in particular every formula unprovable in L has a counterexample in the canonical model.
The main application of canonical models are completeness proofs. Properties of the canonical model of K immediately imply completeness of K with respect to the class of all Kripke frames. This argument does not work for arbitrary L, because there is no guarantee that the underlying frame of the canonical model satisfies the frame conditions of L.
We say that a formula or a set X of formulas is canonical with respect to a property P of Kripke frames, if
- X is valid in every frame which satisfies P,
- for any normal modal logic L which contains X, the underlying frame of the canonical model of L satisfies P.
A union of canonical sets of formulas is itself canonical. It follows from the preceding discussion that any logic axiomatized by a canonical set of formulas is Kripke complete, and compact.
The axioms T, 4, D, B, 5, H, G (and thus any combination of them) are canonical. GL and Grz are not canonical, because they are not compact. The axiom M by itself is not canonical (Goldblatt, 1991), but the combined logic S4.1 (in fact, even K4.1) is canonical.
In general, it is undecidable whether a given axiom is canonical. We know a nice sufficient condition: H. Sahlqvist identified a broad class of formulas (now called Sahlqvist formulas) such that
- a Sahlqvist formula is canonical,
- the class of frames corresponding to a Sahlqvist formula is first-order definable,
- there is an algorithm which computes the corresponding frame condition to a given Sahlqvist formula.
This is a powerful criterion: for example, all axioms listed above as canonical are (equivalent to) Sahlqvist formulas. A logic has the finite model property (FMP) if it is complete with respect to a class of finite frames. An application of this notion is the decidability question: it follows from Post's theorem that a recursively axiomatized modal logic L which has FMP is decidable, provided it is decidable whether a given finite frame is a model of L. In particular, every finitely axiomatizable logic with FMP is decidable.
There are various methods for establishing FMP for a given logic. Refinements and extensions of the canonical model construction often work, using tools such as filtration or unravelling. As another possibility, completeness proofs based on cut-free sequent calculi usually produce finite models directly.
Most of the modal systems used in practice (including all listed above) have FMP.
In some cases, we can use FMP to prove Kripke completeness of a logic: every normal modal logic is complete wrt a class of modal algebras, and a finite modal algebra can be transformed into a Kripke frame. As an example, Robert Bull proved using this method that every normal extension of S4.3 has FMP, and is Kripke complete.
Kripke semantics has a straightforward generalization to logics with more than one modality. A Kripke frame for a language with  as the set of its necessity operators consists of a non-empty set W equipped with binary relations Ri for each i ∈ I. The definition of a satisfaction relation is modified as follows:
as the set of its necessity operators consists of a non-empty set W equipped with binary relations Ri for each i ∈ I. The definition of a satisfaction relation is modified as follows:
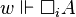 if and only if
if and only if 
A simplified semantics, discovered by Tim Carlson, is often used for polymodal provability logics. A Carlson model is a structure  with a single accessibility relation R, and subsets Di ⊆ W for each modality. Satisfaction is defined as
with a single accessibility relation R, and subsets Di ⊆ W for each modality. Satisfaction is defined as
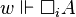 if and only if
if and only if 
Carlson models are easier to visualize and to work with than usual polymodal Kripke models; there are, however, Kripke complete polymodal logics which are Carlson incomplete.
In "Semantical Considerations on Modal Logic", published in 1963, Kripke responded to a difficulty with classical quantification theory. The motivation for the world-relative approach was to represent the possibility that objects in one world may fail to exist in another. If standard quantifier rules are used, however, every term must refer to something that exists in all the possible worlds. This seems incompatible with our ordinary practice of using terms to refer to things that exist contingently.
Kripke's response to this difficulty was to eliminate terms. He gave an example of a system that uses the world-relative interpretation and preserves the classical rules. However, the costs are severe. First, his language is artificially impoverished, and second, the rules for the propositional modal logic must be weakened.
Kripke's possible worlds theory has been used by narratologists (beginning with Pavel and Dolezel) to understand "reader's manipulation of alternative plot developments, or the characters' planned or fantasized alternative action series" (Fludernik). It has become especially useful in the analysis of hyperfiction.[1]
[edit] Intuitionistic Logic
Kripke semantics for the intuitionistic logic follows the same principles as the semantics of modal logic, but it uses a different definition of satisfaction.
An intuitionistic Kripke model is a triple 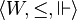 , where
, where 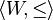 is a partially ordered Kripke frame, and
is a partially ordered Kripke frame, and  satisfies the following conditions:
satisfies the following conditions:
- if p is a propositional variable,
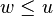 , and
, and  , then
, then 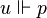 (persistency condition),
(persistency condition), 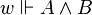 if and only if
if and only if  and
and 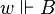 ,
,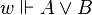 if and only if
if and only if  or
or 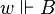 ,
,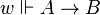 if and only if for all
if and only if for all  ,
,  implies
implies  ,
,- not
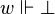 .
.
Intuitionistic logic is sound and complete with respect to its Kripke semantics, and it has FMP.
Intuitionistic first-order logic
Let L be a first-order language. A Kripke model of L is a triple 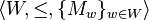 , where
, where 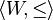 is an intuitionistic Kripke frame, Mw is a (classical) L-structure for each node w ∈ W, and the following compatibility conditions hold whenever u ≤ v:
is an intuitionistic Kripke frame, Mw is a (classical) L-structure for each node w ∈ W, and the following compatibility conditions hold whenever u ≤ v:
- the domain of Mu is included in the domain of Mv,
- realizations of function symbols in Mu and Mv agree on elements of Mu,
- for each n-ary predicate P and elements a1,…,an ∈ Mu: if P(a1,…,an) holds in Mu, then it holds in Mv.
Given an evaluation e of variables by elements of Mw, we define the satisfaction relation ![w\Vdash A[e]](http://upload.wikimedia.org/math/6/2/f/62ff3cbf347580075abb5017c138d439.png) :
:
![w\Vdash P(t_1,\dots,t_n)[e]](http://upload.wikimedia.org/math/0/0/8/008613fbba97474df66193dd70fc3660.png) if and only if
if and only if ![P(t_1[e],\dots,t_n[e])](http://upload.wikimedia.org/math/f/9/4/f94dd65753deaf7a07efd8945c60f903.png) holds in Mw,
holds in Mw,![w\Vdash(A\land B)[e]](http://upload.wikimedia.org/math/5/c/3/5c32c8ff66e43903c094d886eb62f9c9.png) if and only if
if and only if ![w\Vdash A[e]](http://upload.wikimedia.org/math/6/2/f/62ff3cbf347580075abb5017c138d439.png) and
and ![w\Vdash B[e]](http://upload.wikimedia.org/math/2/a/3/2a36882390fea32260733176794f1bac.png) ,
,![w\Vdash(A\lor B)[e]](http://upload.wikimedia.org/math/e/5/a/e5a8eef69125ccdc672b5ec5f2cf95f6.png) if and only if
if and only if ![w\Vdash A[e]](http://upload.wikimedia.org/math/6/2/f/62ff3cbf347580075abb5017c138d439.png) or
or ![w\Vdash B[e]](http://upload.wikimedia.org/math/2/a/3/2a36882390fea32260733176794f1bac.png) ,
,![w\Vdash(A\to B)[e]](http://upload.wikimedia.org/math/4/7/d/47d48866535b57de63579d881eaf9c5d.png) if and only if for all
if and only if for all  ,
, ![u\Vdash A[e]](http://upload.wikimedia.org/math/0/8/f/08f4a2c8e617f89fc58744e072773f2a.png) implies
implies ![u\Vdash B[e]](http://upload.wikimedia.org/math/3/0/6/3064b8f20167dfe3aae90a435ee934b4.png) ,
,- not
![w\Vdash\bot[e]](http://upload.wikimedia.org/math/5/1/4/5143ba452d93efbb3de0e18829fee545.png) ,
, ![w\Vdash(\exists x\,A)[e]](http://upload.wikimedia.org/math/1/1/c/11c1d059fda72a20f9a04df8198d9dd4.png) if and only if there exists an
if and only if there exists an  such that
such that ![w\Vdash A[e(x\to a)]](http://upload.wikimedia.org/math/c/3/a/c3a6fe74cbd57b32732d1e10e300b148.png) ,
,![w\Vdash(\forall x\,A)[e]](http://upload.wikimedia.org/math/c/8/e/c8ecd77f14dd05c86a9e121af82554b2.png) if and only if for every
if and only if for every  and every
and every 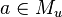 ,
, ![u\Vdash A[e(x\to a)]](http://upload.wikimedia.org/math/c/6/1/c61946a5eb9aa76a8f789e82c8c64b13.png) .
.
Here e(x→a) is the evaluation which gives x the value a, and otherwise agrees with e.
[edit] Naming and necessity
Kripke's three lectures constitute an attack on descriptivist theories of proper names. Kripke attributes variants of descriptivist theories to Frege, Russell, Ludwig Wittgenstein and John Searle, among others. According to descriptivist theories, proper names either are synonymous with descriptions, or have their reference determined by virtue of the name's being associated with a description or cluster of descriptions that an object uniquely satisfies. Kripke rejects both these kinds of descriptivism. He gives several examples purporting to render descriptivism implausible as a theory of how names get their reference determined (e.g., surely Aristotle could have died at age two and so not satisfied any of the descriptions we associate with his name, and yet it would seem wrong to deny that he was Aristotle). As an alternative, Kripke adumbrated a causal theory of reference, according to which a name refers to an object by virtue of a causal connection with the object as mediated through communities of speakers. He points out that proper names, in contrast to most descriptions, are rigid designators: A proper name refers to the named object in every possible world in which the object exists, while most descriptions designate different objects in different possible worlds. For example, 'Nixon' refers to the same person in every possible world in which Nixon exists, while 'the person who won the United States presidential election of 1968' could refer to Nixon, Humphrey, or others in different possible worlds.
Causal theories of reference have also been elaborated and developed by Michael Devitt, Keith Donnellan, David Kaplan, Hilary Putnam, Nathan Salmon, Scott Soames, Gareth Evans, and others, and are perhaps more widely held than descriptivist theories now. Notable holdouts include John Searle, Richard Rorty, and Alonzo Church; also notable is the fact that Hilary Putnam has drawn back from such a completely causal account.
Kripke also raised the prospect of a posteriori necessities — facts that are necessarily true, though they can be known only through empirical investigation. Examples include “Hesperus is Phosphorus”, “Cicero is Tully”, “Water is H2O” and other identity claims where two names refer to the same object.
Finally, Kripke gave an argument against identity materialism in the philosophy of mind, the view that every mental fact is identical with some physical fact (See talk). Kripke argued that the only way to defend this identity is as an a posteriori necessary identity, but that such an identity — e.g., pain is C-fibers firing — could not be necessary, given the possibility of pain that has nothing to do with C-fibers firing. Similar arguments have been proposed by David Chalmers.
Kripke delivered the John Locke lectures in philosophy at Oxford in 1973. Titled Reference and Existence, they are in many respects a continuation of Naming and Necessity, and deal with the subjects of fictional names and perceptual error. They have never been published and the transcript is officially available only in a reading copy in the university philosophy library, which cannot be copied or cited without Kripke's permission. In fact many copies are informally circulated among philosophers. Its influence, though considerable, is thus difficult to trace. However, it has been extensively referred to by some philosophers, particularly Gareth Evans and Nathan Salmon.
In a 1995 paper, philosopher Quentin Smith argued that key concepts in Kripke's new theory of reference had originated from the work of Ruth Barcan Marcus more than a decade earlier.[2] Smith identified six significant ideas to the New Theory which he claimed that Marcus had developed: (1) The idea that proper names are direct references, which don't consist of contained definitions. (2) While one can single out a single thing by a description, this description is not equivalent with a proper name of this thing. (3) The modal argument that proper names are directly referential, and not disguised descriptions. (4) A formal modal logic proof of the necessity of identity. (5) The concept of a rigid designator, although the actual name of the concept was coined by Kripke. (6) The idea of a posteriori identity. Smith proceeded to argue that Kripke failed to understand Marcus' theory at the time, yet later adopted many of its key conceptual themes in his New Theory of Reference. Several scholars have subsequently offered detailed responses arguing that no plagiarism occurred.[3].
[edit] A Puzzle about Belief
Kripke’s main propositions in Naming and Necessity concerning proper names are, that the meaning of a name simply is the object it refers to, and that a name’s referent is determined by a causal link between some sort of “baptism” and the utterance of the name. Nevertheless he acknowledges the possibility that propositions containing names may have some additional semantic properties[4], properties that could explain why two names referring to the same person may give different truth values in propositions about beliefs. (Lois Lane believes that Superman can fly, although she does not believe that Clark Kent can fly. This can be accounted for if the names “Superman” and “Clark Kent”, though referring to the same person, have distinct semantic properties.)
In the article “A Puzzle about Belief” Kripke seems to oppose even this possibility. His argument can be reconstructed in the following way: The idea that two names referring to the same object may have different semantic properties, is supposed to explain that coreferring names behave differently in propositions about beliefs. (Like in Lois Lane's case.) But the same phenomenon occurs even with coreferring names that obviously have the same semantic properties:
Kripke invites us to imagine a French, monolingual boy, Pierre, who believes the following: “Londres est jolie.” (“London is beautiful.”) Pierre moves to London without realising that London = Londres. He then learns English the same way a child would learn the language, that is, not by translating words from French to English. Pierre learns the name “London” from the unattractive part of the city he lives in, so he comes to believe that London is not beautiful. If Kripke’s account is correct Pierre now believes both that London is beautiful and that London is not beautiful. This cannot be explained by coreferring names having different semantic properties. According to Kripke, this shows that attributing additional semantic properties to names, will not explain what it is supposed to explain.
[edit] Wittgenstein
Saul Kripke's Wittgenstein on Rules and Private Language is arguably the most influential and widely discussed interpretation of Wittgenstein's Philosophical Investigations.[5] First published in 1982, the book contends that the central argument of the Philosophical Investigations centers on a devastating rule-following paradox that undermines the possibility of us ever following rules in our use of language. Kripke writes that this paradox is "the most radical and original skeptical problem that philosophy has seen to date" (p. 60). Kripke argues that Wittgenstein does not reject the argument that leads to the rule-following paradox, but accepts it and offers a 'skeptical solution' to ameliorate the paradox's destructive effects. Whilst most commentators accept that the Philosophical Investigations contains the rule-following paradox as Kripke presents it, few have concurred in attributing Kripke's skeptical solution to Wittgenstein. It should be noted that Kripke himself expresses doubts in Wittgenstein on Rules and Private Language as to whether Wittgenstein would endorse his interpretation of the Philosophical Investigations. He says that the work should not be read as an attempt to give an accurate statement of Wittgenstein's views, but rather as an account of Wittgenstein's argument "as it struck Kripke, as it presented a problem for him" (p. 5). The portmanteau "Kripkenstein" has been coined as a jesting nickname for Kripke's reading of the Philosophical Investigations.
(For alternative readings of Wittgenstein, see Colin McGinn's Wittgenstein on Meaning.) The real significance of "Kripkenstein" was to put forward a clear statement of a new kind of scepticism, dubbed "meaning scepticism", which is the idea that for an isolated individual there is no fact in virtue of which he/she means one thing rather than another by the use of a word. Kripke's "sceptical solution" to meaning scepticism is to ground meaning in the behaviour of a community. Kripke's book generated a large secondary literature, divided between those who find his sceptical problem interesting and perceptive, and others (such as Gordon Baker and Peter Hacker) who argue that his meaning scepticism is a pseudo-problem that stems from a confused, selective reading of Wittgenstein. Kripke's position has recently been defended against these and other attacks by the Cambridge philosopher Martin Kusch (2006).
[edit] Truth
In his 1975 article "Outline of a Theory of Truth", Kripke showed that a language can consistently contain its own truth predicate, which was deemed impossible by Alfred Tarski, a pioneer in the area of formal theories of truth. The trick involves letting truth be a partially defined property over the set of grammatically well-formed sentences in the language. Kripke showed how to do this recursively by starting from the set of expressions in a language which do not contain the truth predicate, defining a truth predicate over just that segment: this adds new sentences to the language, and truth is in turn defined for all of them. Unlike Tarski's approach, however, Kripke's lets "truth" be the union of all of these definition-stages; after a denumerable infinity of steps the language reaches a "fixed point" such that using Kripke's method to expand the truth-predicate does not change the language any further. Such a fixed point can then be taken as the basic form of a natural language containing its own truth predicate. But this predicate is undefined for any sentences that do not, so to speak, "bottom out" in simpler sentences not containing a truth predicate. That is, " 'Snow is white' is true" is well-defined, as is " ' "Snow is white" is true' is true," and so forth, but neither "This sentence is true" nor "This sentence is not true" receive truth-conditions; they are, in Kripke's terms, "ungrounded."
[edit] Meaning of "I"
In late January 2006, Kripke attended a conference celebrating his 65th birthday and work at the Graduate Center of the City University of New York, and delivered a 70-minute talk on "The First Person", discussing the meaning and reference of the pronoun "I".[6] [7]
[edit] Religious views
Kripke is a devoutly religious Jew. Additionally, in an interview with Andreas Saugstad, he stated "I don't have the prejudices many have today, I don't believe in a naturalist world view. I don't base my thinking on prejudices or a world view and do not believe in materialism."
[edit] Publications
- 1959. "A Completeness Theorem in Modal Logic", Journal of Symbolic Logic 24(1):1–14.
- 1962. "The Undecidability of Monadic Modal Quantification Theory", Zeitschrift für Mathematische Logik und Grundlagen der Mathematik 8:113–116
- 1963. "Semantical Considerations on Modal Logic", Acta Philosophica Fennica 16:83–94
- 1963. "Semantical Analysis of Modal Logic I: Normal Modal Propositional Calculi", Zeitschrift für Mathematische Logik und Grundlagen der Mathematik 9:67–96
- 1964. "Transfinite Recursions on Admissible Ordinals, I" (abstract), The Journal of Symbolic Logic, Vol. 29, No. 3, p. 162.
- 1964. "Transfinite Recursions on Admissible Ordinals, II" (abstract), The Journal of Symbolic Logic, Vol. 29, No. 3, p. 162.
- 1964. "Admissible Ordinals and the Analytic Hierarchy" (abstract), The Journal of Symbolic Logic, Vol. 29, No. 3, p. 162.
- 1965. "Semantical Analysis of Intuitionistic Logic I", In Formal Systems and Recursive Functions, edited by M. Dummett and J. N. Crossley. Amsterdam: North-Holland Publishing Co.
- 1965. "Semantical Analysis of Modal Logic II: Non-Normal Modal Propositional Calculi", In The Theory of Models, edited by J. W. Addison, L. Henkin and A. Tarski. Amsterdam: North-Holland Publishing Co.
- 1967. "An Extension of a Theorem of Gaifman-Hales-Solovay," Fundamenta Mathematicae, Vol. 61, pp. 29-32.
- 1971. "Identity and Necessity", In Identity and Individuation, edited by M. K. Munitz. New York: New York University Press.
- 1972 (1980). "Naming and Necessity", In Semantics of Natural Language, edited by D. Davidson and G. Harman. Dordrecht; Boston: Reidel. Sets out the causal theory of reference.
- 1975. "Outline of a Theory of Truth", Journal of Philosophy 72:690–716. Sets his theory of truth (against Alfred Tarski), where an object language can contain its own truth predicate.
- 1976. "Is There a Problem about Substitutional Quantification?", In Truth and Meaning: Essays in Semantics, edited by Gareth Evans and John McDowell. Oxford: Oxford University Press.
- 1976. "A Theory of Truth I. Preliminary Report," abstract, Journal of Symbolic Logic, Vol. 41, No. 2, pp. 556.
- 1976. "A Theory of Truth II. Preliminary Report," abstract, Journal of Symbolic Logic, Vol. 41, No. 2, pp. 556-557.
- 1977. "Speaker's Reference and Semantic Reference", Midwest Studies in Philosophy 2:255–276.
- 1979. "A Puzzle about Belief", In Meaning and Use, edited by A. Margalit. Dordrecht and Boston: Reidel.
- 1980. Naming and Necessity. Cambridge, Mass.: Harvard University Press. ISBN 0-674-59845-8 and reprints 1972.
- 1982. Wittgenstein on Rules and Private Language: an Elementary Exposition. Cambridge, Mass.: Harvard University Press. ISBN 0-674-95401-7. Sets out his interpretation of Wittgenstein aka Kripkenstein.
- 1982. "Nonstandard Models of Peano Arithmetic" (with S. Kochen), in Logic and Algorithmics: International Symposium Held in Honor of Ernst Specker, H. Lauchli (ed.), University of Geneva: 277-295.
- 1986. “A Problem in the Theory of Reference: the Linguistic Division of Labor and the Social Character of Naming,” Philosophy and Culture (Proceedings of the XVIIth World Congress of Philosophy), Montreal, Editions Montmorency: 241-247.
- 1992. “Summary: Individual Concepts: Their Logic, Philosophy, and Some of Their Uses.” Proceedings and Addresses of the American Philosophical Association 66: 70-73
- 2005. "Russell's Notion of Scope", Mind 114:1005–1037
- 2008. "Frege’s Theory of Sense and Reference: Some Exegetical Notes,” Theoria 74:181-218
[edit] Unpublished Manuscripts and Online Lectures
- 1971. "Two Paradoxes of Knowledge" (Delivered at the Moral Sciences Club, Cambridge. Transcribed by Elizabeth Anscombe. Some of its ideas are discussed by Thomas Kelly:
http://www.princeton.edu/~tkelly/papers/Beliefpolarizationfinal.pdf )
- 1973. “Vacuous Names and Fictional Entities” (Transcribed by Sam Wheeler and John Troyer)
- 1973. John Locke Lectures: "Reference and Existence". (Transcript available in the Philosophy Library, Oxford University)
- 1975. "Three Lectures on Truth". Princeton University. Discussed by John Burgess: http://www.princeton.edu/~jburgess/Kripke2.doc (see section 9: "Glimpses Beyond")
- 1978. "Time and Identity". Seminar given at Princeton University, 1978. Several versions of this material have circulated. Some of its ideas are discussed by Ted Sider in his book Four-Dimensionalism: An Ontology of Persistence and Time
- 19- "Non-Standard Models and Godel's Theorem: A Model-Theoretic Proof of Godel's Theorem". Summary by Hilary Putnam available at:
- 1984. "Lessons on Functionalism and Automata". (Delivered at the International Wittgenstein Symposium, 1984. Transcribed by Roderick Chisholm. Its main ideas are discussed by Edward P. Stabler: http://www.springerlink.com/content/lr745776l7g24u63/
- 1986. "Nozick on Knowledge". (Manuscript. You can find a discussion of its main ideas at: http://sammelpunkt.philo.at:8080/1493/1/adams.pdf )
- 1986. “Rigid Designation and the Contingent A Priori: The Meter Stick Revisited” (Notre Dame, 1986) Transcript by
- 1988/89. "Seminars on Truth". Three-semester seminar at Princeton in 1988-89, only the first two semesters have been transcribed by Jim Cain. See John Burgess http://www.princeton.edu/~jburgess/Kripke2.doc (footnote 16)
- 19- "Semantical Analysis of Intuitionistic Logic II. Undecidability of the Monadic Fragment" (Undated manuscript)
- 19- "Semantical Analysis of Intuitionistic Logic III" (Undated manuscript)
- 1989. "No Fool's Red? Some Considerations on the Primary/Secondary Quality Distinction"(includes comments by David Velleman). University of Michigan, 1989.
- 1990. "Presupposition and Anaphora". (Delivered at the Interdisciplinary Conference on Linguistic and Philosophical Approaches to the Study of Anaphora, Princeton University, 1990. Transcribed by Richard Holton, Michaelis Michael, and Scott Soames)
- 1992. Whitehead Lectures: "Logicism, Wittgenstein, and De Re Beliefs about Natural Numbers". Delivered at Harvard University, 1992.
- 1992. "Individual Concepts: Their Logic, Philosophy, and Some of Their Uses". Transcribed by Stephen Webb.
- 1996. "Elementary Recursion Theory and its Applications to Formal Systems." Transcribed by Mario Gomez Torrente and John Barker. Index available at: http://74.125.77.132/search?q=cache:y-DdYr9dhj8J:www.phil.uu.nl/~jjoosten/krip/notes/pschomps/Kripke-Frontmatter.ps+saul+kripke+the+road+to+godel&hl=en&ct=clnk&cd=5
- 1999. "The Road to Gödel". (Read at Haifa University, Israel, 1999. Several transcripts exist.
- 2006. "The First Person" The City University of New York, Graduate Center. The videos "The First Person" and "Questions and Answers" are available at: http://web.gc.cuny.edu/Philosophy/events/kripke_conference.html
- 2006. "From Church's Thesis to the First Order Algorithm Theorem," Tel Aviv University, June 13, 2006. Video available at: http://www.vanleer.org.il/eng/videoShow.asp?id=317
Abstract available here: http://portal.acm.org/citation.cfm?id=788022.789011
- 2007. "Roundtable on Externalism" (Hilary Putnam, Tyler Burge, Saul Kripke, and Michael Devitt). University College Dublin, Ireland. Podcast available at: http://www.ucd.ie/news/mar07/030507_Putnam_Award.htm
- 2007. "The Collapse of the Hilbert Program". Indiana University, Presidential Lecture. Video available at: http://broadcast.iu.edu/ceremon/celeb07/index.html
- 2008. "Unrestricted Exportation and Some Morals for the Philosophy of Language," The City University of New York, Graduate Center, May 21, 2008. Podcast available here: http://www1.cuny.edu/portal_ur/news/radio/podcast/lecture_143.mp3
[edit] Interviews and Articles
- "New Frontiers in American Philosophy" by Taylor Branch, New York Times Magazine, August 14, 1977.[2]
- "Saul Kripke, Genius Logician." Interview by Andreas Saugstad, February 25, 2001.[3]
- "Celebrating CUNY's Genius Philosopher" by Gary Shapiro,The New York Sun, January 27, 2006.[4]
- "Philosopher, 65, Lectures Not About 'What Am I?' but 'What Is I?'" by Charles McGrath, The New York Times, January 28, 2006. [5]
[edit] Awards and Recognitions
- Fulbright Scholar (1962-1963)
- Society of Fellows, Harvard University (1963-1966).
- Doctor of Humane Letters, honorary degree, University of Nebraska, 1977.
- Fellow, American Academy of Arts and Sciences (1978--).
- Corresponding Fellow, British Academy (1985--).
- Howard Behrman Award, Princeton University, 1988.
- Fellow, Academia Scientiarum et Artium Europaea (1993--).
- Doctor of Humane Letters, honorary degree, Johns Hopkins University, 1997.
- Doctor of Humane Letters, honorary degree, University of Haifa, Israel, 1998.
- Fellow, Norwegian Academy of Sciences (2000--).
- Schock Prize in Logic and Philosophy, Swedish Academy of Sciences, 2001.
- Doctor of Humane Letters, honorary degree, University of Pennsylvania, 2005.
- Fellow, American Philosophical Society (2005--).
[edit] Literature about Kripke
- Taylor Branch (1977), "New Frontiers in American Philosophy: Saul Kripke". New York Times Magazine.
- Consuelo Preti (2002), On Kripke. Wadsworth. ISBN 0534583660
- Scott Soames (2002), Beyond Rigidity: The Unfinished Semantic Agenda of Naming and Necessity. ISBN 0-19-514529-1.
- Christopher Hughes (2004), Kripke : Names, Necessity, and Identity. ISBN 0-19-824107-0.
- G.W. Fitch (2005), Saul Kripke. ISBN 0-7735-2885-7.
- Martin Kusch (2006), A sceptical Guide to Meaning and Rules. Defending Kripke's Wittgenstein. Acumben: Publishing Limited.
- Arif Ahmed (2007), Saul Kripke. New York, NY; London: Continuum. ISBN 0826492622.
- Christopher Norris (2007), Fiction, Philosophy and Literary Theory: Will the Real Saul Kripke Please Stand Up? London: Continuum
[edit] See also
[edit] References
- ^ Fludernik, Monika. "Histories of Narrative Theory: From Structuralism to Present." A Companion to Narrative Theory. Ed. Phelan and Rabinowitz. Blackwell Publishing, MA:2005.
- ^ Smith, Quentin (2 August 2001). "Marcus, Kripke, and the Origin of the New Theory of Reference". Synthese vol. 104 (no. 2): pp. 179–189. doi:. http://www.qsmithwmu.com/marcus,_kripke,_and_the_origin_of_the_new_theory_of_reference.htm. Retrieved on 2007-05-28.
- ^ Stephen Neale (9 February 2001). "No Plagiarism Here" (.PDF). Times Literary Supplement 104: pp. 12–13. doi:. http://www.rci.rutgers.edu/~neale/papers/NealeKripke.pdf. Retrieved on 2007-05-28.
- ^ Kripke, 1980, p. 20
- ^ Stern, David. Wittgenstein's Philosophical Investigations: an introduction, p. 2
- ^ Charles McGrath (2006-01-28). "Philosopher, 65, Lectures Not About 'What Am I?' but 'What Is I?'". The New York Times. http://www.nytimes.com/2006/01/28/books/28krip.html?pagewanted=1&ei=5088&en=9b8c06355a8dc486&ex=1296104400&adxnnl=0&partner=rssnyt&emc=rss&adxnnlx=1156068875-xI9kVaL9WqHJhRK5STWHrw. Retrieved on 2008-01-23.
- ^ The First Person. Retrieved on 2008-07-20.
[edit] External links
| Wikiquote has a collection of quotations related to: Saul Kripke |
- CUNY faculty page
- Saul Kripke, Genius Logician A short, non-technical interview by Andreas Saugstad, February 25, 2001.
- The conference in honor of Kripke's sixty-fifth birthday with a video of his speech "The First Person", January 25-26, 2006
- Video of his talk "From Church's Thesis to the First Order Algorithm Theorem," June 13, 2006.
- Podcast of his talk "Unrestricted Exportation and Some Morals for the Philosophy of Language," May 21, 2008.
- London Review of Books article by Jerry Fodor discussing Kripke's work
- Celebrating CUNY's Genius Philosopher, by Gary Shapiro, January 27, 2006, in The New York Sun.
- information from 'Philosophy Professor' website
- A New York Times article about his 65th birthday
|
||||||||||||||||||||
|
||||||||||||||

