Russell's paradox
From Wikipedia, the free encyclopedia
|
|
|---|
 Russell in 1907 |
|
|
Part of fundamental mathematics, Russell's paradox (also known as Russell's antinomy), discovered by Bertrand Russell in 1901, showed that the naive set theory of Frege leads to a contradiction.
It might be assumed that, for any formal criterion, a set exists whose members are those objects (and only those objects) that satisfy the criterion; but this assumption is disproved by a set containing exactly the sets that are not members of themselves. If such a set qualifies as a member of itself, it would contradict its own definition as a set containing sets that are not members of themselves. On the other hand, if such a set is not a member of itself, it would qualify as a member of itself by the same definition. This contradiction is Russell's paradox.
In 1908, two ways of avoiding the paradox were proposed, Russell's type theory and Ernst Zermelo's axiomatic set theory, the first consciously constructed axiomatic set theory. Zermelo's axioms went well beyond Frege's axioms of extensionality and unlimited set abstraction, and evolved into the now-canonical Zermelo–Fraenkel set theory (ZFC).
Contents |
[edit] Informal presentation
Let us call a set "abnormal" if it is a member of itself, and "normal" otherwise. For example, take the set of all squares. That set is not itself a square, and therefore is not a member of the set of all squares. So it is "normal". On the other hand, if we take the complementary set that contains all non-squares, that set is itself not a square and so should be one of its own members. It is "abnormal".
Now we consider the set of all normal sets – let us give it a name: R. If R were abnormal, that is, if R were a member of itself, then since R only contains normal sets, R must be normal, which is contradictory to our original hypothesis: R is abnormal. So, R cannot be abnormal, which means R is normal. Further, since every normal set is a member of R, R itself must be a member of R, making R abnormal. Paradoxically, we are led to the contradiction that R is both normal and abnormal.
[edit] Formal derivation
Let R be "the set of all sets that do not contain themselves as members". Formally: A is an element of R if and only if A is not an element of A. In set-builder notation:
Nothing in the system of Frege's Grundgesetze der Arithmetik rules out R being a well-defined set. The problem arises when it is considered whether R is an element of itself. If R is an element of R, then according to the definition R is not an element of R. If R is not an element of R, then R has to be an element of R, again by its very definition. The statements "R is an element of R" and "R is not an element of R" cannot both be true, thus the contradiction.
The following fully formal yet elementary derivation of Russell's paradox[1] makes plain that the paradox requires nothing more than first-order logic with the unrestricted use of set abstraction. The proof is given in terms of collections (all sets are collections, but not conversely). It invokes neither set theory axioms nor the law of excluded middle explicitly or tacitly.
Definition. The collection  , in which
, in which  is any predicate of first-order logic in which
is any predicate of first-order logic in which  is a free variable, denotes the individual
is a free variable, denotes the individual  satisfying
satisfying ![\forall x\,[x \in A \Leftrightarrow \Phi(x)]\,\!](http://upload.wikimedia.org/math/4/1/6/4168daf04b060603dbf7f85a985fa1b7.png) .
.
Theorem. The collection  is contradictory.
is contradictory.
Proof. Replace  in the definition of collection by
in the definition of collection by 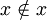 , so that the implicit definition of
, so that the implicit definition of 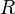 becomes
becomes ![\forall x\,[x \in R \Leftrightarrow x \notin x].\,\!](http://upload.wikimedia.org/math/c/6/8/c685296f8e5f8688ac353fa46e9d8660.png) Instantiating
Instantiating  by
by 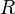 then yields the contradiction
then yields the contradiction 
Remark. The above definition and theorem are the first theorem and definition in Potter (2004), consistent with the fact that Russell's paradox requires no set theory whatsoever. Incidentally, the force of this argument cannot be evaded by simply proscribing the substitution of 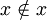 for
for  . In fact, there are denumerably many formulae
. In fact, there are denumerably many formulae  giving rise to the paradox.[2] For some examples, see reciprocation below.
giving rise to the paradox.[2] For some examples, see reciprocation below.
[edit] The paradox holds in intuitionistic logic
Often derivations of Russell's paradox employ the law of the excluded middle (Russell's own derivation did). Thus it may be tempting to conclude that the paradox is avoided if the law of excluded middle is disallowed, as with intuitionistic logic. However, as is clear from the first of the two informal arguments presented above, the law of excluded middle is not needed for the paradoxical argument. Here we show that the paradox can still be generated formally by means of the intuitionistically valid law of non-contradiction.
Theorem. The collection  is contradictory even if the background logic is intuitionistic.
is contradictory even if the background logic is intuitionistic.
Proof. From the definition of 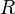 , we have that
, we have that 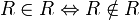 . Then
. Then 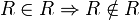 (biconditional elimination). But also
(biconditional elimination). But also  (the law of identity), so
(the law of identity), so  . But by the law of non-contradiction we know that
. But by the law of non-contradiction we know that  . By modus tollens we conclude
. By modus tollens we conclude  .
.
But since 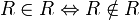 , we also have that
, we also have that 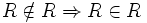 , and so we also conclude
, and so we also conclude  by modus ponens. Hence we have deduced both
by modus ponens. Hence we have deduced both  and its negation using only intuitionistically valid methods.
and its negation using only intuitionistically valid methods. 
More simply, it is intuitionistically impossible for a proposition to be equivalent to its negation. Assume P ⇔ ¬P. Then P ⇒ ¬P. Hence ¬P. Symmetrically, we can derive ¬¬P, using ¬P ⇒ P. So we have inferred both ¬P and its negation from our assumption, with no use of excluded middle.
[edit] Reciprocation
Russell's paradox arises from the supposition that one can meaningfully define a class in terms of any well-defined property Φ(x); that is, that we can form the set P = {x | Φ(x) is true }. When we take  , we get Russell's paradox. This is only the simplest of many possible variations of this theme.
, we get Russell's paradox. This is only the simplest of many possible variations of this theme.
For example, if one takes  , one gets a similar paradox; there is no set P of all x with this property. For convenience, let us agree to call a set S reciprocated if there is a set T with
, one gets a similar paradox; there is no set P of all x with this property. For convenience, let us agree to call a set S reciprocated if there is a set T with 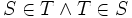 ; then P, the set of all non-reciprocated sets, does not exist. If
; then P, the set of all non-reciprocated sets, does not exist. If  , we would immediately have a contradiction, since P is reciprocated (by itself) and so should not belong to P. But if
, we would immediately have a contradiction, since P is reciprocated (by itself) and so should not belong to P. But if 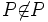 , then P is reciprocated by some set Q, so that we have
, then P is reciprocated by some set Q, so that we have  , and then Q is also a reciprocated set, and so
, and then Q is also a reciprocated set, and so  , another contradiction.
, another contradiction.
Any of the variations of Russell's paradox described above can be reformulated to use this new paradoxical property. For example, the reformulation of the Grelling paradox is as follows. Let us agree to call an adjective P "nonreciprocated" if and only if there is no adjective Q such that both P describes Q and Q describes P. Then one obtains a paradox when one asks if the adjective "nonreciprocated" is itself nonreciprocated.
This can also be extended to longer chains of mutual inclusion. We may call sets A1,A2,...,An a chain of set A1 if 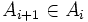 for i=1,2,...,n-1. A chain can be infinite (in which case each Ai has an infinite chain). Then we take the set P of all sets which have no infinite chain, from which it follows that P itself has no infinite chain. But then
for i=1,2,...,n-1. A chain can be infinite (in which case each Ai has an infinite chain). Then we take the set P of all sets which have no infinite chain, from which it follows that P itself has no infinite chain. But then  , so in fact P has the infinite chain P,P,P,... which is a contradiction. This is known as Mirimanoff's paradox.
, so in fact P has the infinite chain P,P,P,... which is a contradiction. This is known as Mirimanoff's paradox.
[edit] Set-theoretic responses
In 1908, Ernst Zermelo proposed an axiomatization of set theory that avoided the paradoxes of naive set theory by replacing arbitrary set comprehension with weaker existence axioms, such as his axiom of separation (Aussonderung). Modifications to this axiomatic theory proposed in the 1920s by Abraham Fraenkel, Thoralf Skolem, and by Zermelo himself resulted in the axiomatic set theory called ZFC. This theory became widely accepted once Zermelo's axiom of choice ceased to be controversial, and ZFC has remained the canonical axiomatic set theory down to the present day.
ZFC does not assume that, for every property, there is a set of all things satisfying that property. Rather, it asserts that given any set X, any subset of X definable using first-order logic exists. The object R discussed above cannot be constructed in this fashion, and is therefore not a ZFC set. In some extensions of ZFC, objects like R are called proper classes. ZFC is silent about types, although some argue that Zermelo's axioms tacitly presuppose a background type theory.
Through the work of Zermelo and others, especially John von Neumann, the structure of what some see as the "natural" objects described by ZFC eventually became clear; they are the elements of the von Neumann universe, V, built up from the empty set by transfinitely iterating the power set operation. It is thus now possible again to reason about sets in a non-axiomatic fashion without running afoul of Russell's paradox, namely by reasoning about the elements of V. Whether it is appropriate to think of sets in this way is a point of contention among the rival points of view on the philosophy of mathematics.
Other resolutions to Russell's paradox, more in the spirit of type theory, include the axiomatic set theories New Foundations and Scott-Potter set theory.
[edit] History
Exactly when Russell discovered the paradox is not known. It seems to have been May or June 1901, probably as a result of his work on Cantor's theorem that the number of entities in a certain domain is smaller than the number of subclasses of those entities.[3] He first mentioned the paradox in a 1901 paper in the International Monthly, entitled "Recent work in the philosophy of mathematics." He also mentioned Cantor's proof that there is no greatest cardinal, adding that "the master" had been guilty of a subtle fallacy that he would discuss later. Russell also mentioned the paradox in his Principles of Mathematics (not to be confused with the later Principia Mathematica), calling it "The Contradiction."[4] Again, he said that he was led to it by analyzing Cantor's "no greatest cardinal" proof.
Famously, Russell wrote to Frege about the paradox in June 1902, just as Frege was preparing the second volume of his Grundgesetze der Arithmetik.[5] Frege hurriedly wrote an appendix admitting to the paradox, and proposed a solution that was later proved unsatisfactory. In any event, after publishing the second volume of the Grundgesetze, Frege wrote little on mathematical logic and the philosophy of mathematics.
Zermelo states, in footnote in section c of his axiomatic set theory published in 1908, that he discovered the paradox independently of Russell, and that he communicated it by letter to Hilbert, prior to its publication by Russell in 1903. It is also known that unpublished discussions of set theoretical paradoxes took place in the mathematical community at the turn of the century.
In 1923, Ludwig Wittgenstein proposed to "dispose" of Russell's paradox as follows:
"The reason why a function cannot be its own argument is that the sign for a function already contains the prototype of its argument, and it cannot contain itself. For let us suppose that the function F(fx) could be its own argument: in that case there would be a proposition 'F(F(fx))', in which the outer function F and the inner function F must have different meanings, since the inner one has the form O(f(x)) and the outer one has the form Y(O(fx)). Only the letter 'F' is common to the two functions, but the letter by itself signifies nothing. This immediately becomes clear if instead of 'F(Fu)' we write '(do) : F(Ou) . Ou = Fu'. That disposes of Russell's paradox." (Tractatus Logico-Philosophicus, 3.333)
Russell and Alfred North Whitehead wrote their three-volume Principia Mathematica (PM) hoping to achieve what Frege had been unable to do. They sought to banish the paradoxes of naive set theory by employing a theory of types they devised for this purpose. While they succeeded in grounding arithmetic in a fashion, it is not at all evident that they did so by purely logical means. While PM avoided the known paradoxes and allows the derivation of a great deal of mathematics, its system gave rise to new problems.
In any event, Kurt Gödel in 1930–31 proved that while the logic of much of PM, now known as first-order logic, is complete, Peano arithmetic is necessarily incomplete if it is consistent. This is very widely – though not universally – regarded as having shown the logicist program of Frege to be impossible to complete.
[edit] Applied versions
There are some versions of this paradox that are closer to real-life situations and may be easier to understand for non-logicians. For example, the Barber paradox supposes a barber who shaves men if and only if they do not shave themselves. When one thinks about whether the barber should shave himself or not, the paradox begins to emerge.
As another example, consider five lists of encyclopedia entries within the same encyclopedia:
| List of articles about people: | List of articles starting with the letter L:
...
... |
List of articles about places: | List of articles about Japan: | List of all lists that do not contain themselves:
...
...
|
If the "List of all lists that do not contain themselves" contains itself, then it does not belong to itself and should be removed. However, if it does not list itself, then it should be added to itself.
While appealing, these layman's versions of the paradox share a drawback: an easy refutation of the Barber paradox seems to be that such a barber does not exist, or at least does not shave (a variant of which is that the barber is a woman). The whole point of Russell's paradox is that the answer "such a set does not exist" means the definition of the notion of set within a given theory is unsatisfactory. Note the difference between the statements "such a set does not exist" and "such a set is empty".
A notable exception to the above may be the Grelling-Nelson paradox, in which words and meaning are the elements of the scenario rather than people and hair-cutting. Though it is easy to refute the Barber's paradox by saying that such a barber does not (and cannot) exist, it is impossible to say something similar about a meaningfully defined word.
One way that the paradox has been dramatised is as follows:
Suppose that every public library has to compile a catalog of all its books. The catalog is itself one of the library's books, but while some librarians include it in the catalog for completeness, others leave it out, as being self-evident.
Now imagine that all these catalogs are sent to the national library. Some of them include themselves in their listings, others do not. The national librarian compiles two master catalogs - one of all the catalogs that list themselves, and one of all those which don't.
The question is now, should these catalogs list themselves? The 'Catalog of all catalogs that list themselves' is no problem. If the librarian doesn't include it in its own listing, it is still a true catalog of those catalogs that do include themselves. If he does include it, it remains a true catalog of those that list themselves.
However, just as the librarian cannot go wrong with the first master catalog, he is doomed to fail with the second. When it comes to the 'Catalog of all catalogs that don't list themselves', the librarian cannot include it in its own listing, because then it would belong in the other catalog, that of catalogs that do include themselves. However, if the librarian leaves it out, the catalog is incomplete. Either way, it can never be a true catalog of catalogs that do not list themselves.
[edit] Applications and related topics
The Barber paradox, in addition to leading to a tidier set theory, has been used twice more with great success: Kurt Gödel proved his incompleteness theorem by formalizing the paradox, and Turing proved the undecidability of the Halting problem (and with that the Entscheidungsproblem) by using the same trick.
[edit] Russell-like paradoxes
As illustrated above for the Barber paradox, Russell's paradox is not hard to extend. Take:
- A transitive verb <V>, that can be applied to its substantive form.
Form the sentence:
- The <V>er that <V>s all (and only those) who don't <V> themselves,
Sometimes the "all" is replaced by "all <V>ers".
An example would be "paint":
- The painter that paints all (and only those) that don't paint themselves.
or "elect"
- The elector (representative), that elects all that don't elect themselves.
Paradoxes that fall in this scheme include:
- The barber with "shave".
- The original Russell's paradox with "contain": The container (Set) that contains all (containers) that don't contain themselves.
- The Grelling-Nelson paradox with "describer": The describer (word) that describes all words, that don't describe themselves.
- Richard's paradox with "denote": The denoter (number) that denotes all denoters (numbers) that don't denote themselves. (In this paradox, all descriptions of numbers get an assigned number. The term "that denotes all denoters (numbers) that don't denote themselves" is here called Richardian.)
- "Groucho's Paradox": Groucho Marx said that he would never belong to a club that would accept him as a member.
[edit] Related paradoxes
- The liar paradox and Epimenides paradox, whose origins are ancient.
- The Kleene-Rosser paradox, showing that the original lambda calculus is inconsistent, by means of a self-negating statement.
- Curry's paradox (named after Haskell Curry) which does not require negation.
- The smallest uninteresting integer paradox.
[edit] See also
- Self-reference
- Universal set
- On Denoting, one of Russell's first attempts at critiquing Frege
[edit] Footnotes
- ^ Adapted from Potter (2004: 24-25).
- ^ See Willard Quine, 1938, "On the theory of types," Journal of Symbolic Logic 3.
- ^ In modern terminology, the cardinality of a set is strictly less than that of its power set.
- ^ Russell, Bertrand (1903). Principles of Mathematics. Cambridge: Cambridge University Press. Chapter X, section 100. ISBN 0-393-31404-9.
- ^ Russell's letter and Frege's reply are translated in Jean van Heijenoort, 1967, and in Frege’s Philosophical and Mathematical Correspondence.
[edit] References
- Potter, Michael, 2004. Set Theory and its Philosophy. Oxford Univ. Press.
[edit] External links
- Stanford Encyclopedia of Philosophy: "Russell's Paradox" -- by A. D. Irvine.
- Russell's Paradox at cut-the-knot
- Some paradoxes - an anthology


