Table of mathematical symbols
From Wikipedia, the free encyclopedia
Contents |
[edit] Common symbols
This is a listing of common symbols found within all branches of the science of mathematics.
| Symbol (HTML) |
Symbol (TeX) |
Name | Explanation | Examples |
|---|---|---|---|---|
| Read as | ||||
| Category | ||||
|
=
|
 |
equality | x = y means x and y represent the same thing or value. | 1 + 1 = 2 |
| is equal to; equals | ||||
| everywhere | ||||
|
≠
|
 |
inequation | x ≠ y means that x and y do not represent the same thing or value. (As ≠ can be hard to type, the more “keyboard friendly” forms !=, /= or <> may be seen. These are avoided in mathematical texts.) |
2 + 2 ≠ 5 |
| is not equal to; does not equal | ||||
| everywhere | ||||
|
<
> ≪ ≫ |
  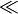 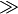 |
strict inequality | x < y means x is less than y. x > y means x is greater than y. x ≪ y means x is much less than y. x ≫ y means x is much greater than y. |
3 < 4 5 > 4 0.003 ≪ 1000000 |
| is less than, is greater than, is much less than, is much greater than | ||||
| order theory | ||||
|
≤
≥ |
  |
inequality | x ≤ y means x is less than or equal to y. x ≥ y means x is greater than or equal to y. (As ≤ and ≥ can be hard to type, the more “keyboard friendly” forms <= and >= may be seen. These are avoided in mathematical texts.) |
3 ≤ 4 and 5 ≤ 5 5 ≥ 4 and 5 ≥ 5 |
| is less than or equal to, is greater than or equal to | ||||
| order theory | ||||
|
∝
|
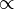 |
proportionality | y ∝ x means that y = kx for some constant k. | if y = 2x, then y ∝ x |
| is proportional to; varies as | ||||
| everywhere | ||||
|
+
|
 |
addition | 4 + 6 means the sum of 4 and 6. | 2 + 7 = 9 |
| plus | ||||
| arithmetic | ||||
| disjoint union | A1 + A2 means the disjoint union of sets A1 and A2. | A1 = {1, 2, 3, 4} ∧ A2 = {2, 4, 5, 7} ⇒ A1 + A2 = {(1,1), (2,1), (3,1), (4,1), (2,2), (4,2), (5,2), (7,2)} |
||
| the disjoint union of ... and ... | ||||
| set theory | ||||
|
−
|
 |
subtraction | 9 − 4 means the subtraction of 4 from 9. | 8 − 3 = 5 |
| minus | ||||
| arithmetic | ||||
| negative sign | −3 means the negative of the number 3. | −(−5) = 5 | ||
| negative; minus; the opposite of | ||||
| arithmetic | ||||
| set-theoretic complement | A − B means the set that contains all the elements of A that are not in B. (∖ can also be used for set-theoretic complement as described below.) |
{1,2,4} − {1,3,4} = {2} | ||
| minus; without | ||||
| set theory | ||||
|
×
|
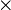 |
multiplication | 3 × 4 means the multiplication of 3 by 4. | 7 × 8 = 56 |
| times | ||||
| arithmetic | ||||
| Cartesian product | X×Y means the set of all ordered pairs with the first element of each pair selected from X and the second element selected from Y. | {1,2} × {3,4} = {(1,3),(1,4),(2,3),(2,4)} | ||
| the Cartesian product of ... and ...; the direct product of ... and ... | ||||
| set theory | ||||
| cross product | u × v means the cross product of vectors u and v | (1,2,5) × (3,4,−1) = (−22, 16, − 2) |
||
| cross | ||||
| vector algebra | ||||
| group of units | R× consists of the set of units of the ring R, along with the operation of multiplication. This may also be written R* as described below, or U(R). |
![\begin{align} (\mathbb{Z} / 5\mathbb{Z})^\times & = \{ [1], [2], [3], [4] \} \\ & \cong C_4 \\ \end{align}](http://upload.wikimedia.org/math/0/6/f/06f5c6ec9c5a7c6e00e8fd5e18529e9e.png) |
||
| the group of units of | ||||
| ring theory | ||||
|
·
|
 |
multiplication | 3 · 4 means the multiplication of 3 by 4. | 7 · 8 = 56 |
| times | ||||
| arithmetic | ||||
| dot product | u · v means the dot product of vectors u and v | (1,2,5) · (3,4,−1) = 6 | ||
| dot | ||||
| vector algebra | ||||
|
÷
⁄ |
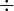 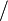 |
division | 6 ÷ 3 or 6 ⁄ 3 means the division of 6 by 3. | 2 ÷ 4 = .5 12 ⁄ 4 = 3 |
| divided by | ||||
| arithmetic | ||||
| quotient group | G / H means the quotient of group G modulo its subgroup H. | {0, a, 2a, b, b+a, b+2a} / {0, b} = {{0, b}, {a, b+a}, {2a, b+2a}} | ||
| mod | ||||
| group theory | ||||
| quotient set | A/~ means the set of all ~ equivalence classes in A. | If we define ~ by x ~ y ⇔ x − y ∈ ℤ, then ℝ/~ = {x + n : n ∈ ℤ : x ∈ (0,1]} |
||
| mod | ||||
| set theory | ||||
|
±
|
 |
plus-minus | 6 ± 3 means both 6 + 3 and 6 − 3. | The equation x = 5 ± √4, has two solutions, x = 7 and x = 3. |
| plus or minus | ||||
| arithmetic | ||||
| plus-minus | 10 ± 2 or equivalently 10 ± 20% means the range from 10 − 2 to 10 + 2. | If a = 100 ± 1 mm, then a ≥ 99 mm and a ≤ 101 mm. | ||
| plus or minus | ||||
| measurement | ||||
|
∓
|
 |
minus-plus | 6 ± (3 ∓ 5) means both 6 + (3 − 5) and 6 − (3 + 5). | cos(x ± y) = cos(x) cos(y) ∓ sin(x) sin(y). |
| minus or plus | ||||
| arithmetic | ||||
|
√
|
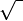 |
square root | 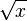 means the positive number whose square is x. means the positive number whose square is x. |
 |
| the principal square root of; square root | ||||
| real numbers | ||||
| complex square root | if  is represented in polar coordinates with is represented in polar coordinates with  , then , then 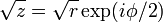 . . |
 |
||
| the complex square root of …; square root | ||||
| complex numbers | ||||
|
|…|
|
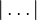 |
absolute value or modulus | |x| means the distance along the real line (or across the complex plane) between x and zero. | |3| = 3 |–5| = |5| = 5 | i | = 1 | 3 + 4i | = 5 |
| absolute value (modulus) of | ||||
| numbers | ||||
| Euclidean distance | |x – y| means the Euclidean distance between x and y. | For x = (1,1), and y = (4,5), |x – y| = √([1–4]2 + [1–5]2) = 5 |
||
| Euclidean distance between; Euclidean norm of | ||||
| geometry | ||||
| determinant | |A| means the determinant of the matrix A |  |
||
| determinant of | ||||
| matrix theory | ||||
| cardinality (AKA order) | |X| means the cardinality of the set X. (# or ♯ may be used instead as described below.) |
|{3, 5, 7, 9}| = 4. | ||
| cardinality of; size of | ||||
| set theory | ||||
|
||…||
|
 |
norm | || x || means the norm of the element x of a normed vector space. | || x + y || ≤ || x || + || y || |
| norm of; length of | ||||
| linear algebra | ||||
| nearest integer function | ||x|| means the nearest integer to x, with half-integers being rounded to even. (This may also be written [x], ⌊x⌉, nint(x) or Round(x).) |
||1|| = 1, ||1.5|| = 2, ||−2.5|| = 2, ||3.49|| = 3 | ||
| nearest integer to | ||||
| numbers | ||||
|
∣
∤ |
  |
divisor, divides | a|b means a divides b. As with inequality, this symbol can be difficult to type and its negation is rare, in which case a regular but slightly shorter vertical bar "|" character is used. |
Since 15 = 3×5, it is true that 3|15 and 5|15. |
| divides | ||||
| number theory | ||||
| conditional probability | P(A|B) means the probability of the event a occurring given that b occurs. | If P(A)=0.4 and P(B)=0.5, P(A|B)=((0.4)(0.5))/(0.5)=0.4 | ||
| given | ||||
| probability | ||||
| restriction | f|A means the function f restricted to the set A, that is, it is the function with domain A ∩ dom(f) that agrees with f. | The function f : R → R defined by f(x) = x2 is not injective, but f|R+ is injective. | ||
| restriction of … to …; restricted to | ||||
| set theory | ||||
|
||
|
 |
parallel | x || y means x is parallel to y. | If l || m and m ⊥ n then l ⊥ n. In physics this is also used to express  . . |
| is parallel to | ||||
| geometry, physics | ||||
| incomparability | x || y means x is incomparable to y. | {1,2} || {2,3} under set containment. | ||
| is incomparable to | ||||
| order theory | ||||
| exact divisibility | pa || n means pa exactly divides n (i.e. pa divides n but pa+1 does not). | 23 || 360. | ||
| exactly divides | ||||
| number theory | ||||
|
#
♯ |
  |
cardinality (AKA order) | #X means the cardinality of the set X. (|…| may be used instead as described above.) |
#{4, 6, 8} = 3 |
| cardinality of; size of | ||||
| set theory | ||||
|
:
|
 |
such that | : means “such that”, and is used in proofs and the set-builder notation (described below). | ∃ n ∈ ℕ: n is even. |
| such that; so that | ||||
| everywhere | ||||
| field extension | K : F means the field K extends the field F. This may also be written as K ≥ F. |
ℝ : ℚ | ||
| extends; over | ||||
| field theory | ||||
| inner product of matrices | A : B means the inner product of the matrices A and B. The general inner product is denoted by 〈u, v〉, 〈u | v〉 or (u | v), as described below. For spatial vectors, the dot product notation, x·y is common. See also Bra-ket notation. |
 |
||
| inner product of | ||||
| linear algebra | ||||
|
!
|
 |
factorial | n! means the product 1 × 2 × ... × n. | 4! = 1 × 2 × 3 × 4 = 24 |
| factorial | ||||
| combinatorics | ||||
| logical negation | The statement !A is true if and only if A is false. A slash placed through another operator is the same as "!" placed in front. (The symbol ! is primarily from computer science. It is avoided in mathematical texts, where the notation ¬A is preferred.) |
!(!A) ⇔ A x ≠ y ⇔ !(x = y) |
||
| not | ||||
| propositional logic | ||||
|
~
|
 |
probability distribution | X ~ D, means the random variable X has the probability distribution D. | X ~ N(0,1), the standard normal distribution |
| has distribution | ||||
| statistics | ||||
| row equivalence | A~B means that B can be generated by using a series of elementary row operations on A |  |
||
| is row equivalent to | ||||
| matrix theory | ||||
| same order of magnitude | m ~ n means the quantities m and n have the same order of magnitude, or general size. (Note that ~ is used for an approximation that is poor, otherwise use ≈ .) |
2 ~ 5 8 × 9 ~ 100 but π2 ≈ 10 |
||
| roughly similar; poorly approximates | ||||
| approximation theory | ||||
| asymptotically equivalent | f ~ g means  . . |
x ~ x+1 |
||
| is asymptotically equivalent to | ||||
| asymptotic analysis | ||||
| equivalence relation | a ~ b means ![b \in [a]](http://upload.wikimedia.org/math/6/7/6/6769b7a159bc917be1478849db21b7ae.png) (and equivalently (and equivalently ![a \in [b]](http://upload.wikimedia.org/math/3/e/c/3ec8d0d70da247252e9aa1380a011f27.png) ). ). |
1 ~ 5 mod 4 |
||
| are in the same equivalence class | ||||
| everywhere | ||||
|
≈
|
 |
approximately equal | x ≈ y means x is approximately equal to y. | π ≈ 3.14159 |
| is approximately equal to | ||||
| everywhere | ||||
| isomorphism | G ≈ H means that group G is isomorphic (structurally identical) to group H. (≅ can also be used for isomorphic, as described below.) |
Q / {1, −1} ≈ V, where Q is the quaternion group and V is the Klein four-group. |
||
| is isomorphic to | ||||
| group theory | ||||
|
≀
|
 |
wreath product | A ≀ H means the wreath product of the group A by the group H. This may also be written A wr H. |
 is isomorphic to the automorphism group of the complete bipartite graph on (n,n) vertices. is isomorphic to the automorphism group of the complete bipartite graph on (n,n) vertices. |
| wreath product of … by … | ||||
| group theory | ||||
|
◅
|
 |
normal subgroup | N ◅ G means that N is a normal subgroup of group G. | Z(G) ◅ G |
| is a normal subgroup of | ||||
| group theory | ||||
| ideal | I ◅ R means that I is an ideal of ring R. | (2) ◅ Z | ||
| is an ideal of | ||||
| ring theory | ||||
|
∴
|
 |
therefore | Sometimes used in proofs before logical consequences. | All humans are mortal. Socrates is a human. ∴ Socrates is mortal. |
| therefore; so; hence | ||||
| everywhere | ||||
|
∵
|
 |
because | Sometimes used in proofs before reasoning. | 3331 is prime ∵ it has no positive integer factors other than itself and one. |
| because; since | ||||
| everywhere | ||||
|
⇒
→ ⊃ |
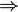  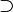 |
material implication | A ⇒ B means if A is true then B is also true; if A is false then nothing is said about B. (→ may mean the same as ⇒, or it may have the meaning for functions given below.) (⊃ may mean the same as ⇒, or it may have the meaning for superset given below.) |
x = 2 ⇒ x2 = 4 is true, but x2 = 4 ⇒ x = 2 is in general false (since x could be −2). |
| implies; if … then | ||||
| propositional logic, Heyting algebra | ||||
|
⇔
↔ |
  |
material equivalence | A ⇔ B means A is true if B is true and A is false if B is false. | x + 5 = y +2 ⇔ x + 3 = y |
| if and only if; iff | ||||
| propositional logic | ||||
|
¬
˜ |
 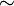 |
logical negation | The statement ¬A is true if and only if A is false. A slash placed through another operator is the same as "¬" placed in front. (The symbol ~ has many other uses, so ¬ or the slash notation is preferred. Computer scientists will often use ! but this is avoided in mathematical texts.) |
¬(¬A) ⇔ A x ≠ y ⇔ ¬(x = y) |
| not | ||||
| propositional logic | ||||
|
∧
|
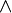 |
logical conjunction or meet in a lattice | The statement A ∧ B is true if A and B are both true; else it is false. For functions A(x) and B(x), A(x) ∧ B(x) is used to mean min(A(x), B(x)). |
n < 4 ∧ n >2 ⇔ n = 3 when n is a natural number. |
| and; min; meet | ||||
| propositional logic, lattice theory | ||||
| wedge product | u ∧ v means the wedge product of vectors u and v. This generalizes the cross product to higher dimensions. (For vectors in R3, × can also be used.) |
 |
||
| wedge product; exterior product | ||||
| linear algebra | ||||
|
∨
|
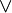 |
logical disjunction or join in a lattice | The statement A ∨ B is true if A or B (or both) are true; if both are false, the statement is false. For functions A(x) and B(x), A(x) ∨ B(x) is used to mean max(A(x), B(x)). |
n ≥ 4 ∨ n ≤ 2 ⇔ n ≠ 3 when n is a natural number. |
| or; max; join | ||||
| propositional logic, lattice theory | ||||
|
⊕
⊻ |
  |
exclusive or | The statement A ⊕ B is true when either A or B, but not both, are true. A ⊻ B means the same. | (¬A) ⊕ A is always true, A ⊕ A is always false. |
| xor | ||||
| propositional logic, Boolean algebra | ||||
| direct sum | The direct sum is a special way of combining several modules into one general module (the symbol ⊕ is used, ⊻ is only for logic). | Most commonly, for vector spaces U, V, and W, the following consequence is used: U = V ⊕ W ⇔ (U = V + W) ∧ (V ∩ W = {0}) |
||
| direct sum of | ||||
| abstract algebra | ||||
|
∀
|
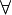 |
universal quantification | ∀ x: P(x) means P(x) is true for all x. | ∀ n ∈ ℕ: n2 ≥ n. |
| for all; for any; for each | ||||
| predicate logic | ||||
|
∃
|
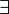 |
existential quantification | ∃ x: P(x) means there is at least one x such that P(x) is true. | ∃ n ∈ ℕ: n is even. |
| there exists; there is; there are | ||||
| predicate logic | ||||
|
∃!
|
 |
uniqueness quantification | ∃! x: P(x) means there is exactly one x such that P(x) is true. | ∃! n ∈ ℕ: n + 5 = 2n. |
| there exists exactly one | ||||
| predicate logic | ||||
|
:=
≡ :⇔ ≜ ≝ ≐ |
      |
definition | x := y or x ≡ y means x is defined to be another name for y, under certain assumptions taken in context. (Some writers use ≡ to mean congruence). P :⇔ Q means P is defined to be logically equivalent to Q. |
 |
| is defined as; equal by definition | ||||
| everywhere | ||||
|
≅
|
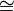 |
congruence | △ABC ≅ △DEF means triangle ABC is congruent to (has the same measurements as) triangle DEF. | |
| is congruent to | ||||
| geometry | ||||
| isomorphic | G ≅ H means that group G is isomorphic (structurally identical) to group H. (≈ can also be used for isomorphic, as described above.) |
 . . |
||
| is isomorphic to | ||||
| abstract algebra | ||||
|
≡
|
 |
congruence relation | a ≡ b (mod n) means a − b is divisible by n | 5 ≡ 11 (mod 3) |
| ... is congruent to ... modulo ... | ||||
| modular arithmetic | ||||
|
{ , }
|
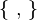 |
set brackets | {a,b,c} means the set consisting of a, b, and c. | ℕ = { 1, 2, 3, …} |
| the set of … | ||||
| set theory | ||||
|
{ : }
{ | } |
  |
set builder notation | {x : P(x)} means the set of all x for which P(x) is true. {x | P(x)} is the same as {x : P(x)}. | {n ∈ ℕ : n2 < 20} = { 1, 2, 3, 4} |
| the set of … such that | ||||
| set theory | ||||
|
∅
{ } |
   |
empty set | ∅ means the set with no elements. { } means the same. | {n ∈ ℕ : 1 < n2 < 4} = ∅ |
| the empty set | ||||
| set theory | ||||
|
∈
∉ |
  |
set membership | a ∈ S means a is an element of the set S; a ∉ S means a is not an element of S. | (1/2)−1 ∈ ℕ 2−1 ∉ ℕ |
| is an element of; is not an element of | ||||
| everywhere, set theory | ||||
|
⊆
⊂ |
  |
subset | (subset) A ⊆ B means every element of A is also an element of B. (proper subset) A ⊂ B means A ⊆ B but A ≠ B. (Some writers use the symbol ⊂ as if it were the same as ⊆.) |
(A ∩ B) ⊆ A ℕ ⊂ ℚ ℚ ⊂ ℝ |
| is a subset of | ||||
| set theory | ||||
|
⊇
⊃ |
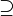 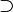 |
superset | A ⊇ B means every element of B is also element of A. A ⊃ B means A ⊇ B but A ≠ B. (Some writers use the symbol ⊃ as if it were the same as ⊇.) |
(A ∪ B) ⊇ B ℝ ⊃ ℚ |
| is a superset of | ||||
| set theory | ||||
|
∪
|
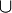 |
set-theoretic union | A ∪ B means the set of those elements which are either in A, or in B, or in both. | A ⊆ B ⇔ (A ∪ B) = B |
| the union of … or …; union | ||||
| set theory | ||||
|
∩
|
 |
set-theoretic intersection | A ∩ B means the set that contains all those elements that A and B have in common. | {x ∈ ℝ : x2 = 1} ∩ ℕ = {1} |
| intersected with; intersect | ||||
| set theory | ||||
|
∆
|
 |
symmetric difference | A ∆ B means the set of elements in exactly one of A or B. | {1,5,6,8} ∆ {2,5,8} = {1,2,6} |
| symmetric difference | ||||
| set theory | ||||
|
∖
|
 |
set-theoretic complement | A ∖ B means the set that contains all those elements of A that are not in B. (− can also be used for set-theoretic complement as described above.) |
{1,2,3,4} ∖ {3,4,5,6} = {1,2} |
| minus; without | ||||
| set theory | ||||
|
→
|
 |
function arrow | f: X → Y means the function f maps the set X into the set Y. | Let f: ℤ → ℕ∪{0} be defined by f(x) := x2. |
| from … to | ||||
| set theory, type theory | ||||
|
↦
|
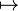 |
function arrow | f: a ↦ b means the function f maps the element a to the element b. | Let f: x ↦ x+1 (the successor function). |
| maps to | ||||
| set theory | ||||
|
∘
|
 |
function composition | fog is the function, such that (fog)(x) = f(g(x)). | if f(x) := 2x, and g(x) := x + 3, then (fog)(x) = 2(x + 3). |
| composed with | ||||
| set theory | ||||
|
ℕ
N |
  |
natural numbers | N means either { 0, 1, 2, 3, ...} or { 1, 2, 3, ...}. The choice depends on the area of mathematics being studied; e.g. number theorists prefer the latter; analysts, set theorists and computer scientists prefer the former. To avoid confusion, always check an author's definition of N. Set theorists often use the notation ω to denote the set of natural numbers (including zero), along with the standard ordering relation ≤. |
ℕ = {|a| : a ∈ ℤ} |
| N; the (set of) natural numbers | ||||
| numbers | ||||
|
ℤ
Z |
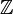  |
integers | ℤ means {..., −3, −2, −1, 0, 1, 2, 3, ...}.
ℤ+ or ℤ> means {1, 2, 3, ...} . ℤ≥ means {0, 1, 2, 3, ...} . |
ℤ = {p, −p : p ∈ ℕ ∪ {0}} |
| Z; the (set of) integers | ||||
| numbers | ||||
|
ℤn
ℤp Zn Zp |
    |
integers mod n | ℤn means {[0], [1], [2], ...[n−1]} with addition and multiplication modulo n. Note that any letter may be used instead of n, such as p. To avoid confusion with p-adic numbers, use ℤ/pℤ or ℤ/(p) instead. |
ℤ3 = {[0], [1], [2]} |
| Zn; the (set of) integers modulo n | ||||
| numbers | ||||
| p-adic integers | Note that any letter may be used instead of p, such as n or l. |
|||
| the (set of) p-adic integers | ||||
| numbers | ||||
|
ℚ
Q |
  |
rational numbers | ℚ means {p/q : p ∈ ℤ, q ∈ ℕ}. | 3.14000... ∈ ℚ π ∉ ℚ |
| Q; the (set of) rational numbers; the rationals | ||||
| numbers | ||||
|
ℝ
R |
  |
real numbers | ℝ means the set of real numbers. | π ∈ ℝ √(−1) ∉ ℝ |
| R; the (set of) real numbers; the reals | ||||
| numbers | ||||
|
ℂ
C |
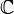  |
complex numbers | ℂ means {a + b i : a,b ∈ ℝ}. | i = √(−1) ∈ ℂ |
| C; the (set of) complex numbers | ||||
| numbers | ||||
|
𝕂
K |
  |
real or complex numbers | K means both R and C: a statement containing K is true if either R or C is substituted for the K. |  |
| K | ||||
| linear algebra | ||||
|
∞
|
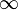 |
infinity | ∞ is an element of the extended number line that is greater than all real numbers; it often occurs in limits. |  |
| infinity | ||||
| numbers | ||||
|
⌊…⌋
|
 |
floor | ⌊x⌋ means the floor of x, i.e. the largest integer less than or equal to x. (This may also be written [x], floor(x) or int(x).) |
⌊4⌋ = 4, ⌊2.1⌋ = 2, ⌊2.9⌋ = 2, ⌊−2.6⌋ = −3 |
| floor; greatest integer; entier | ||||
| numbers | ||||
|
⌈…⌉
|
 |
ceiling | ⌈x⌉ means the ceiling of x, i.e. the smallest integer greater than or equal to x. (This may also be written ceil(x) or ceiling(x).) |
⌈4⌉ = 4, ⌈2.1⌉ = 3, ⌈2.9⌉ = 3, ⌈−2.6⌉ = −2 |
| ceiling | ||||
| numbers | ||||
|
⌊…⌉
|
 |
nearest integer function | ⌊x⌉ means the nearest integer to x, with half-integers being rounded to even. (This may also be written [x], ||x||, nint(x) or Round(x).) |
⌊2⌉ = 2, ⌊2.5⌉ = 2, ⌊3.5⌉ = 3, ⌊4.5⌉ = 4, ⌊7.2⌉ = 7, ⌊8.9⌉ = 9 |
| nearest integer to | ||||
| numbers | ||||
|
[ : ]
|
![[\ :\ ] \!\,](http://upload.wikimedia.org/math/3/9/d/39d5340377c7738ba4f72a9739f63afe.png) |
degree of a field extension | [K : F] means the degree of the extension K : F. | [ℚ(√2) : ℚ] = 2 [ℂ : ℝ] = 2 [ℝ : ℚ] = ∞ |
| the degree of | ||||
| field theory | ||||
|
[ ]
[ , ] [ , , ] |
![[\ ] \!\,](http://upload.wikimedia.org/math/c/2/d/c2dc57d3486acdb1ec8efad3719a2757.png) ![[\ ,\ ] \!\,](http://upload.wikimedia.org/math/6/9/1/691075e7366c90a8857edd45a2053aa8.png) ![[\ ,\ ,\ ] \!\,](http://upload.wikimedia.org/math/f/2/a/f2a7f66d6e7f58cba58ee0148f6b824e.png) |
equivalence class | [a] means the equivalence class of a, i.e. {x : x ~ a}, where ~ is an equivalence relation. [a]R means the same, but with R as the equivalence relation. |
Let a ~ b be true iff a ≡ b (mod 5).
Then [2] = {…, −8, −3, 2, 7, …}. |
| the equivalence class of | ||||
| abstract algebra | ||||
| floor | [x] means the floor of x, i.e. the largest integer less than or equal to x. (This may also be written ⌊x⌋, floor(x) or int(x). Not to be confused with the nearest integer function, as described below.) |
[3] = 3, [3.5] = 3, [3.99] = 3, [−3.7] = −4 | ||
| floor; greatest integer; entier | ||||
| numbers | ||||
| nearest integer function | [x] means the nearest integer to x, with half-integers being rounded to even. (This may also be written ⌊x⌉, ||x||, nint(x) or Round(x). Not to be confused with the floor function, as described above.) |
[2] = 2, [2.5] = 2, [3.5] = 4, [4.5] = 4 | ||
| nearest integer to | ||||
| numbers | ||||
| closed interval | ![[a,b] = \{x \in \mathbb{R} : a \le x \le b \}](http://upload.wikimedia.org/math/d/6/f/d6fb4b1478e9c68e216dcf78d4941dca.png) . . |
[0,1] | ||
| closed interval | ||||
| order theory | ||||
| commutator | [g, h] = g−1h−1gh (or ghg−1h−1), if g, h ∈ G (a group). [a, b] = ab − ba, if a, b ∈ R (a ring or commutative algebra). |
xy = x[x, y] (group theory). [AB, C] = A[B, C] + [A, C]B (ring theory). |
||
| the commutator of | ||||
| group theory, ring theory | ||||
| triple scalar product | [a, b, c] = a × b · c, the scalar product of a × b with c. | [a, b, c] = [b, c, a] = [c, a, b]. | ||
| the triple scalar product of | ||||
| vector calculus | ||||
|
( )
( , ) |
  |
function application | f(x) means the value of the function f at the element x. | If f(x) := x2, then f(3) = 32 = 9. |
| of | ||||
| set theory | ||||
| precedence grouping | Perform the operations inside the parentheses first. | (8/4)/2 = 2/2 = 1, but 8/(4/2) = 8/2 = 4. | ||
| parentheses | ||||
| everywhere | ||||
| tuple | An ordered list (or sequence, or horizontal vector, or row vector) of values.
(Note that the notation (a,b) is ambiguous: it could be an ordered pair or an open interval.) |
(a, b) is an ordered pair (or 2-tuple).
(a, b, c) is an ordered triple (or 3-tuple). ( ) is the empty tuple (or 0-tuple). |
||
| tuple; n-tuple; ordered pair/triple/etc; row vector | ||||
| everywhere | ||||
| highest common factor | (a, b) means the highest common factor of a and b. (This may also be written hcf(a, b) or gcd(a, b).) |
(3, 7) = 1 (they are coprime); (15, 25) = 5. | ||
| highest common factor; greatest common divisor; hcf; gcd | ||||
| number theory | ||||
|
( , )
] , [ |
 ![]\ ,\ [ \!\,](http://upload.wikimedia.org/math/5/6/a/56ae0d842e03b2b7504f316f176a3467.png) |
open interval |  . .
(Note that the notation (a,b) is ambiguous: it could be an ordered pair or an open interval. The notation ]a,b[ can be used instead.) |
(4,18) |
| open interval | ||||
| order theory | ||||
|
( , ]
] , ] |
![(\ ,\ ] \!\,](http://upload.wikimedia.org/math/b/2/2/b2217c84cbe375b0506b8429a6f69258.png) ![]\ ,\ ] \!\,](http://upload.wikimedia.org/math/1/f/1/1f129e23b31f26cf551000acaed7e18c.png) |
left-open interval | ![(a,b] = \{x \in \mathbb{R} : a < x \le b \}](http://upload.wikimedia.org/math/d/a/9/da9d325123d50dbc4e36363f2863ce3e.png) . . |
(−1, 7] and (−∞, −1] |
| half-open interval; left-open interval | ||||
| order theory | ||||
|
[ , )
[ , [ |
  |
right-open interval |  . . |
[4, 18) and [1, +∞) |
| half-open interval; right-open interval | ||||
| order theory | ||||
|
〈〉
<> 〈,〉 <,> |
    |
inner product | 〈u,v〉 means the inner product of u and v, where u and v are members of an inner product space. Note that the notation 〈u, v〉 may be ambiguous: it could mean the inner product or the linear span. There are many variants of the notation, such as 〈u | v〉 and (u | v), which are described below. The less-than and greater-than symbols are primarily from computer science; they are avoided in mathematical texts. For spatial vectors, the dot product notation, x·y is common. For matrices, the colon notation A : B may be used. |
The standard inner product between two vectors x = (2, 3) and y = (−1, 5) is: 〈x, y〉 = 2 × −1 + 3 × 5 = 13 |
| inner product of | ||||
| linear algebra | ||||
| linear span | 〈S〉 means the span of S ⊆ V. That is, it is the intersection of all subspaces of V which contain S. 〈u1, u2, …〉is shorthand for 〈{u1, u2, …}〉.
|
 . . |
||
| (linear) span of; linear hull of |
||||
| linear algebra | ||||
| subgroup generated by a set | 〈S〉 means the smallest subgroup of G (where S ⊆ G, a group) containing every element of S. 〈g1, g2, …〉is shorthand for 〈{g1, g2, …}〉. |
In S3, 〈(1 2)〉 = {id, (1 2)} and 〈(1 2 3)〉 = {id, (1 2 3), (1 3 2)}. | ||
| the subgroup generated by | ||||
| group theory | ||||
|
〈|〉
<|> (|) |
   |
inner product | 〈u | v〉 means the inner product of u and v, where u and v are members of an inner product space. (u | v) means the same. Another variant of the notation is 〈u, v〉 which is described above. The less-than and greater-than symbols are primarily from computer science; they are avoided in mathematical texts. For spatial vectors, the dot product notation, x·y is common. For matrices, the colon notation A : B may be used. |
|
| inner product of | ||||
| linear algebra | ||||
|
∑
|
 |
summation |  means a1 + a2 + … + an. means a1 + a2 + … + an. |
 = 12 + 22 + 32 + 42 = 12 + 22 + 32 + 42
|
| sum over … from … to … of | ||||
| arithmetic | ||||
|
∏
|
 |
product | 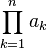 means a1a2···an. means a1a2···an. |
 = (1+2)(2+2)(3+2)(4+2) = (1+2)(2+2)(3+2)(4+2)
|
| product over … from … to … of | ||||
| arithmetic | ||||
| Cartesian product |  means the set of all (n+1)-tuples means the set of all (n+1)-tuples
|
 |
||
| the Cartesian product of; the direct product of | ||||
| set theory | ||||
|
∐
|
 |
coproduct | A general construction which subsumes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the "least specific" object to which each object in the family admits a morphism. | |
| coproduct over … from … to … of | ||||
| category theory | ||||
|
′
• |
  |
derivative | f ′(x) means the derivative of the function f at the point x, i.e., the slope of the tangent to f at x. The dot notation indicates a time derivative. That is |
If f(x) := x2, then f ′(x) = 2x |
| … prime derivative of |
||||
| calculus | ||||
|
∫
|
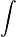 |
indefinite integral or antiderivative | ∫ f(x) dx means a function whose derivative is f. | ∫x2 dx = x3/3 + C |
| indefinite integral of the antiderivative of |
||||
| calculus | ||||
| definite integral | ∫ab f(x) dx means the signed area between the x-axis and the graph of the function f between x = a and x = b. | ∫ab x2 dx = b3/3 − a3/3; | ||
| integral from … to … of … with respect to | ||||
| calculus | ||||
|
∮
|
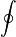 |
contour integral or closed line integral | Similar to the integral, but used to denote a single integration over a closed curve or loop. It is sometimes used in physics texts involving equations regarding Gauss's Law, and while these formulas involve a closed surface integral, the representations describe only the first integration of the volume over the enclosing surface. Instances where the latter requires simultaneous double integration, the symbol ∯ would be more appropriate. A third related symbol is the closed volume integral, denoted by the symbol ∰.
The contour integral can also frequently be found with a subscript capital letter C, ∮C, denoting that a closed loop integral is, in fact, around a contour C, or sometimes dually appropriately, a circle C. In representations of Gauss's Law, a subscript capital S, ∮S, is used to denote that the integration is over a closed surface. |
If C is a Jordan curve about 0, then  . . |
| contour integral of | ||||
| calculus | ||||
|
∇
|
 |
gradient | ∇f (x1, …, xn) is the vector of partial derivatives (∂f / ∂x1, …, ∂f / ∂xn). | If f (x,y,z) := 3xy + z², then ∇f = (3y, 3x, 2z) |
| del, nabla, gradient of | ||||
| vector calculus | ||||
| divergence |  |
If  , then , then  . . |
||
| del dot, divergence of | ||||
| vector calculus | ||||
| curl |   |
If  , then , then  . . |
||
| curl of | ||||
| vector calculus | ||||
|
∂
|
 |
partial derivative | ∂f/∂xi means the partial derivative of f with respect to xi, where f is a function on (x1, …, xn). | If f(x,y) := x2y, then ∂f/∂x = 2xy |
| partial, d | ||||
| calculus | ||||
| boundary | ∂M means the boundary of M | ∂{x : ||x|| ≤ 2} = {x : ||x|| = 2} | ||
| boundary of | ||||
| topology | ||||
| degree of a polynomial | ∂f means the degree of the polynomial f. (This may also be written deg f.) |
∂(x2 − 1) = 2 | ||
| degree of | ||||
| algebra | ||||
|
δ
|
 |
Dirac delta function |  |
δ(x) |
| Dirac delta of | ||||
| hyperfunction | ||||
| Kronecker delta | 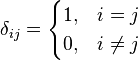 |
δij | ||
| Kronecker delta of | ||||
| hyperfunction | ||||
|
<:
<· |
  |
cover | x <• y means that x is covered by y. | {1, 8} <• {1, 3, 8} among the subsets of {1, 2, …, 10} ordered by containment. |
| is covered by | ||||
| order theory | ||||
| subtype | T1 <: T2 means that T1 is a subtype of T2. | If S <: T and T <: U then S <: U (transitivity). | ||
| is a subtype of | ||||
| type theory | ||||
|
T
|
 |
transpose | AT means A, but with its rows swapped for columns. This may also be written At or Atr. |
If A = (aij) then AT = (aji). |
| transpose | ||||
| matrix operations | ||||
|
⊤
|
 |
top element | ⊤ means the largest element of a lattice. | ∀x : x ∨ ⊤ = ⊤ |
| the top element | ||||
| lattice theory | ||||
| top type | ⊤ means the top or universal type; every type in the type system of interest is a subtype of top. | ∀ types T, T <: ⊤ | ||
| the top type; top | ||||
| type theory | ||||
|
⊥
|
 |
perpendicular | x ⊥ y means x is perpendicular to y; or more generally x is orthogonal to y. | If l ⊥ m and m ⊥ n in the plane then l || n. |
| is perpendicular to | ||||
| geometry | ||||
| orthogonal complement | W⊥ means the orthogonal complement of W (where W is a subspace of the inner product space V), the set of all vectors in V orthogonal to every vector in W. | Within  , ,  . . |
||
| orthogonal/perpendicular complement of; perp | ||||
| linear algebra | ||||
| coprime | x ⊥ y means x has no factor in common with y. | 34 ⊥ 55. | ||
| is coprime to | ||||
| number theory | ||||
| bottom element | ⊥ means the smallest element of a lattice. | ∀x : x ∧ ⊥ = ⊥ | ||
| the bottom element | ||||
| lattice theory | ||||
| bottom type | ⊥ means the bottom type (a.k.a. the zero type or empty type); bottom is the subtype of every type in the type system. | ∀ types T, ⊥ <: T | ||
| the bottom type; bot | ||||
| type theory | ||||
| comparability | x ⊥ y means that x is comparable to y. | {e, π} ⊥ {1, 2, e, 3, π} under set containment. | ||
| is comparable to | ||||
| order theory | ||||
|
⊧
|
 |
entailment | A ⊧ B means the sentence A entails the sentence B, that is in every model in which A is true, B is also true. | A ⊧ A ∨ ¬A |
| entails | ||||
| model theory | ||||
|
⊢
|
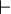 |
inference | x ⊢ y means y is derivable from x. | A → B ⊢ ¬B → ¬A. |
| infers; is derived from | ||||
| propositional logic, predicate logic | ||||
|
⊗
|
 |
tensor product, tensor product of modules |  means the tensor product of V and U. means the tensor product of V and U.  means the tensor product of modules V and U over the ring R. means the tensor product of modules V and U over the ring R. |
{1, 2, 3, 4} ⊗ {1, 1, 2} = {{1, 2, 3, 4}, {1, 2, 3, 4}, {2, 4, 6, 8}} |
| tensor product of | ||||
| linear algebra | ||||
|
*
|
 |
convolution | f * g means the convolution of f and g. |  . . |
| convolution, convolved with | ||||
| functional analysis | ||||
| complex conjugate | z* means the complex conjugate of z. (  can also be used for the conjugate of z, as described below.) can also be used for the conjugate of z, as described below.) |
 . . |
||
| conjugate | ||||
| complex numbers | ||||
| group of units | R* consists of the set of units of the ring R, along with the operation of multiplication. This may also be written R× as described above, or U(R). |
![\begin{align} (\mathbb{Z} / 5\mathbb{Z})^\ast & = \{ [1], [2], [3], [4] \} \\ & \cong C_4 \\ \end{align}](http://upload.wikimedia.org/math/0/1/c/01ce87251f2bb444b7e41b0592df6de8.png) |
||
| the group of units of | ||||
| ring theory | ||||
|
x
|
 |
mean | 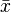 (often read as “x bar”) is the mean (average value of xi). (often read as “x bar”) is the mean (average value of xi). |
 . . |
| overbar, … bar | ||||
| statistics | ||||
| complex conjugate |  means the complex conjugate of z. means the complex conjugate of z.(z* can also be used for the conjugate of z, as described above.) |
 . . |
||
| conjugate | ||||
| complex numbers | ||||
| algebraic closure |  is the algebraic closure of the field F. is the algebraic closure of the field F. |
The field of algebraic numbers is sometimes denoted as  because it is the algebraic closure of the rational numbers because it is the algebraic closure of the rational numbers  . . |
||
| algebraic closure of | ||||
| field theory | ||||
| topological closure |  is the topological closure of the set S. is the topological closure of the set S.This may also be denoted as cl(S) or Cl(S). |
In the space of the real numbers,  (the rational numbers are dense in the real numbers). (the rational numbers are dense in the real numbers). |
||
| (topological) closure of | ||||
| topology |
[edit] Advanced and less-frequently used math symbols
Here are some other math symbols in a compact list, preceded by their Unicode values
- x2135: ℵ: Hebrew letter aleph, the sign for cardinality
- x2210 ∐: direct sum, but in other areas of math, it might mean the coproduct
- x22c9 ⋉: semidirect product
[edit] Note on symbol names
One symbol can have up to four different names in standard web publishing. For example, the Unicode symbol known as "Subset of or equal to" can be expressed as:
- Unicode: ⊆ rendered as ⊆ or as the raw Unicode character ⊆ in the wikitext
- HTML: ⊆ rendered as ⊆
- TeX (LaTex, MathML): \subseteq rendered as
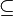
- Postscript (Adobe, PDF) name: reflexsubset. The Postscript name is of interest if you are viewing a raw PDF 1.3 or earlier version files or other low-level issue. See Symbol (typeface) is some Postscript names that one will find if one examines PDF files. (see PostScript Language Reference Manual, pp. 256-257, "Symbol Font").
Some useful cross-references via Unicode are:
- Short list of commonly used LaTeX symbols and Comprehensive LaTeX Symbol List
- MathML Characters - sorts out Unicode, HTML and MathML/TeX names on one page
- Unicode values and MathML names
- Unicode values and Postscript names from the source code for Ghostscript
[edit] Abbreviated function names
There are a typical set of abbreviations used for functions whose names.
Operators borrowed from linear algebra include:
- char = characteristic
- det = determinant
- dim = dimension (vector space)
- Card = cardinality (AKA order)
and from category theory:
- Ker = kernel (category theory)
- Im = Image (mathematics)
- Tr or trace = field trace
and from other areas of abstract algebra:
- = , → See Exact functor, Topological half-exact functor
- δ = Delta functor
- End = Endomorphism ring
- Ext = Ext functor (extension of modules)
- Frob = Frobenius endomorphism
- Hom = Hom functor
- Spec = spectrum of a ring
- Sym = symmetric group
- Sym2 = symmetric square
- Tan = tangent space
- Tor = Tor functor (torsion)
- general and special linear groups are referred to with the acronyms SL, GL, PSL and PGL.
[edit] See also
- Greek letters used in mathematics
- ISO 31-11
- Mathematical alphanumeric symbols
- Mathematical notation
- Notation in probability and statistics
- Physical constants
- Roman letters used in mathematics
- Table of logic symbols
- Unicode Mathematical Operators
- Wikipedia:Mathematical symbols
- Help:Advanced editing#Special characters
- Help:Displaying a formula
 .
.
