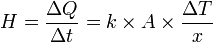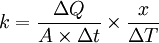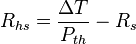Thermal conductivity

From Wikipedia, the free encyclopedia

Jump to: navigation, search
 It has been suggested that R-value (insulation) be merged into this article or section. (Discuss)

In physics, thermal conductivity, k, is the property of a material that indicates its ability to conduct heat. It appears primarily in Fourier's Law for heat conduction.

First, we define heat conduction by the formula:

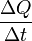H=\frac{\Delta Q}{\Delta t}=k\times A\times\frac{\Delta T}{x}

where \frac{\Delta Q}{\Delta t} is the rate of heat flow, k is the thermal conductivity, A is the total cross sectional area of conducting surface, ΔT is temperature difference and x is the thickness of conducting surface separating the 2 temperatures.

Thus, rearranging the equation gives thermal conductivity,

k=\frac{\Delta Q}{\Delta t}\times\frac{1}{A}\times\frac{x}{\Delta T}

(Note: \frac{\Delta T}{x} is the temperature gradient)

In other words, it is defined as the quantity of heat, ΔQ, transmitted during time Δt through a thickness x, in a direction normal to a surface of area A, due to a temperature difference ΔT, under steady state conditions and when the heat transfer is dependent only on the temperature gradient.

Alternatively, it can be thought of as a flux of heat (energy per unit area per unit time) divided by a temperature gradient (temperature difference per unit length)

k=\frac{\Delta Q}{A\times{} \Delta t}\times\frac{x}{\Delta T}

Typical units are SI: W/(m·K) and English units: Btu/(hr·ft·°F). To convert between the two, use the relation 1 Btu/(hr·ft·°F) = 1.730735 W/(m·K). [Perry's Chemical Engineers' Handbook, 7th Edition, Table 1-4]

Contents

[edit] Examples

In metals, thermal conductivity approximately tracks electrical conductivity according to the Wiedemann-Franz law, as freely moving valence electrons transfer not only electric current but also heat energy. However, the general correlation between electrical and thermal conductance does not hold for other materials, due to the increased importance of phonon carriers for heat in non-metals. As shown in the table below, highly electrically conductive silver is less thermally conductive than diamond, which is a electrical insulator.

Thermal conductivity depends on many properties of a material, notably its structure and temperature. For instance, pure crystalline substances exhibit very different thermal conductivities along different crystal axes, due to differences in phonon coupling along a given crystal axis. Sapphire is a notable example of variable thermal conductivity based on orientation and temperature, with 35 W/(m·K) along the c-axis and 32 W/(m·K) along the a-axis.[1]

Air and other gases are generally good insulators, in the absence of convection. Therefore, many insulating materials function simply by having a large number of gas-filled pockets which prevent large-scale convection. Examples of these include expanded and extruded polystyrene (popularly referred to as "styrofoam") and silica aerogel. Natural, biological insulators such as fur and feathers achieve similar effects by dramatically inhibiting convection of air or water near an animal's skin.

Light gases, such as hydrogen and helium typically have high thermal conductivity. Dense gases such as xenon and dichlorodifluoromethane have low thermal conductivity. An exception, sulfur hexafluoride, a dense gas, has a relatively high thermal conductivity due to its high heat capacity. Argon, a gas denser than air, is often used in insulated glazing (double paned windows) to improve their insulation characteristics.

Thermal conductivity is important in building insulation and related fields. However, materials used in such trades are rarely subjected to chemical purity standards. Several construction materials' k values are listed below. These should be considered approximate due to the uncertainties related to material definitions.

The following table is meant as a small sample of data to illustrate the thermal conductivity of various types of substances. For more complete listings of measured k-values, see the references.

[edit] List of thermal conductivity values

Main article: List of thermal conductivities

This is a list of approximate values of thermal conductivity, k, for some common materials. Please consult the list of thermal conductivities for more accurate values, references and detailed information.

Material Thermal conductivity
W/(m·K)
Silica Aerogel 0.004 - 0.04
Air 0.025
Wood 0.04 - 0.4
Hollow Fill Fibre Insulation Polartherm 0.042
Alcohols and oils 0.1 - 0.21
Polypropene 0.12 [1]
Mineral oil 0.138
Rubber 0.16
LPG 0.23 - 0.26
Cement, Portland 0.29
Epoxy (silica-filled) 0.30
Epoxy (unfilled) 0.59
Water (liquid) 0.6
Thermal grease 0.7 - 3
Thermal epoxy 1 - 7
Glass 1.1
Soil 1.5
Concrete, stone 1.7
Ice 2
Sandstone 2.4
Stainless steel 12.11 ~ 45.0
Lead 35.3
Aluminium 220 (pure)
120--180 (alloys)
Gold 318
Copper 380
Silver 429
Diamond 900 - 2320

[edit] Controlling Resistance

Often in heat transfer the concept of controlling resistance is used to determine how to either increase or decrease heat transfer. Heat transfer coefficients represent how much heat is able to transfer through a defined region of a heat transfer area. The inverse of these coefficients are the resistances of those areas. If a wall can be considered, it would have a heat transfer coefficient representing convection on each side of the wall, and one representing conduction through the wall. To obtain an overall heat transfer coefficient, the resistances need to be summed up.

\frac{1}{U}={\Sigma}\frac{1}{h} + {\Sigma}{R} = \frac{1}{h_1} + \frac{1}{h_2} + \frac{1}{h_3} + ... + {R_1} + {R_2} + {R_3} + ...

Due to the nature of the above reciprocal relation, the smallest heat transfer coefficient (h) or the largest resistance is generally the controlling resistance as it dominates the other terms to the point that varying the other resistances will have little impact on the overall resistance:

\frac{1}{U} \approx \frac{1}{h_i} or Ri

Thus the controlling resistance can be used to both simplify heat transfer calculations and manipulate a system to a desired resistance value.

[edit] Measurement

Main article: Thermal conductivity measurement

Generally speaking, there are a number of possibilities to measure thermal conductivity, each of them suitable for a limited range of materials, depending on the thermal properties and the medium temperature. A distinction may be observed between steady-state and transient techniques.

In general, steady-state techniques perform a measurement when the temperature of the material measured does not change with time. This makes the signal analysis straightforward (steady state implies constant signals). The disadvantage is that a well-engineered experimental setup is usually needed. The Divided Bar (various types) is the most common device used for consolidated rock samples.

The transient techniques perform a measurement during the process of heating up. The advantage is that measurements can be made relatively quickly. Transient methods are usually carried out by needle probes (inserted into samples or plunged into the ocean floor).

For good conductors of heat, Searle's bar method can be used.[2] For poor conductors of heat, Lees' disc method can be used.[3] An alternative traditional method using real thermometers is described at [4]. A brief review of new methods measuring thermal conductivity, thermal diffusivity and specific heat within a single measurement is available at [5]. A thermal conductance tester, one of the instruments of gemology, determines if gems are genuine diamonds using diamond's uniquely high thermal conductivity.

[edit] Standard Measurement Techniques

  • IEEE Standard 98-2002, "Standard for the Preparation of Test Procedures for the Thermal Evaluation of Solid Electrical Insulating Materials", ISBN 0-7381-3277-2 [7]
  • ASTM Standard D5470-06, "Standard Test Method for Thermal Transmission Properties of Thermally Conductive Electrical Insulation Materials" [8]
  • ASTM Standard E1225-04, "Standard Test Method for Thermal Conductivity of Solids by Means of the Guarded-Comparative-Longitudinal Heat Flow Technique" [9]
  • ASTM Standard D5930-01, "Standard Test Method for Thermal Conductivity of Plastics by Means of a Transient Line-Source Technique" [10]
  • ASTM Standard D2717-95, "Standard Test Method for Thermal Conductivity of Liquids" [11]
  • ISO 22007-2:2008 "Plastics -- Determination of thermal conductivity and thermal diffusivity -- Part 2: Transient plane heat source (hot disc) method" [12]

[edit] Difference between US and European notation

What is called the k-value of construction materials (e.g. window glass) in the US, is called λ-value in Europe.

What is called U-value (= the inverse of R-value) in the US, used to be called k-value in Europe, but is now also called U-value in Europe.

K-value (with capital k) refers in Europe to the total isolation value of a building. K-value is obtained by multiplying the form factor of the building (= the total inward surface of the outward walls of the building divided by the total volume of the building) with the average U-value of the outward walls of the building. K-value is therefore expressed as (m2·m-3)·(W·K-1·m-2) = W·K-1·m-3. A house with a volume of 400 m³ and a K-value of 0.45 (the new European norm. It is commonly referred to as K45) will therefore theoretically require 180 W to maintain its interior temperature 1 K above exterior temperature. So, to maintain the house at 20 °C when it is freezing outside (0 °C), 3600 W of continuous heating is required.

[edit] Related terms

The reciprocal of thermal conductivity is thermal resistivity, measured in kelvin-metres per watt (K·m·W−1).

When dealing with a known amount of material, its thermal conductance and the reciprocal property, thermal resistance, can be described. Unfortunately there are differing definitions for these terms.

[edit] Thermal conductance

For general scientific use, thermal conductance is the quantity of heat that passes in unit time through a plate of particular area and thickness when its opposite faces differ in temperature by one kelvin. For a plate of thermal conductivity k, area A and thickness L this is kA/L, measured in W·K−1 (equivalent to: W/°C). Thermal conductivity and conductance are analogous to electrical conductivity (A·m−1·V−1) and electrical conductance (A·V−1).

There is also a measure known as heat transfer coefficient: the quantity of heat that passes in unit time through unit area of a plate of particular thickness when its opposite faces differ in temperature by one kelvin. The reciprocal is thermal insulance. In summary:

  • thermal conductance = kA/L, measured in W·K−1
    • thermal resistance = L/kA, measured in K·W−1 (equivalent to: °C/W)
  • heat transfer coefficient = k/L, measured in W·K−1·m−2
    • thermal insulance = L/k, measured in K·m²·W−1.

The heat transfer coefficient is also known as thermal admittance

[edit] Thermal Resistance

When thermal resistances occur in series, they are additive. So when heat flows through two components each with a resistance of 1 °C/W, the total resistance is 2 °C/W.

A common engineering design problem involves the selection of an appropriate sized heat sink for a given heat source. Working in units of thermal resistance greatly simplifies the design calculation. The following formula can be used to estimate the performance:

R_{hs} = \frac {\Delta T}{P_{th}} - R_s

where:

  • Rhs is the maximum thermal resistance of the heat sink to ambient, in °C/W
  • ΔT is the temperature difference (temperature drop), in °C
  • Pth is the thermal power (heat flow), in Watts
  • Rs is the thermal resistance of the heat source, in °C/W

For example, if a component produces 100 W of heat, and has a thermal resistance of 0.5 °C/W, what is the maximum thermal resistance of the heat sink? Suppose the maximum temperature is 125 °C, and the ambient temperature is 25 °C; then the ΔT is 100 °C. The heat sink's thermal resistance to ambient must then be 0.5 °C/W or less.

[edit] Alternate definition (buildings)

When dealing with buildings, thermal resistance or R-value means what is described above as thermal insulance, and thermal conductance means the reciprocal. For materials in series, these thermal resistances (unlike conductances) can simply be added to give a thermal resistance for the whole.

A third term, thermal transmittance, incorporates the thermal conductance of a structure along with heat transfer due to convection and radiation. It is measured in the same units as thermal conductance and is sometimes known as the composite thermal conductance. The term U-value is another synonym.

In summary, for a plate of thermal conductivity k (the k value [2]), area A and thickness L:

  • thermal conductance = k/L, measured in W·K−1·m−2;
  • thermal resistance (R value) = L/k, measured in K·m²·W−1;
  • thermal transmittance (U value) = 1/(Σ(L/k)) + convection + radiation, measured in W·K−1·m−2.

[edit] Textile industry

In textiles, a tog value may be quoted as a measure of thermal resistance in place of a measure in SI units.

[edit] Origins

In applied science and engineering in real-world systems, heat flux is virtually impossible to perfectly control and isolate, so the preceding formulas are quite accurate relative to the system from a macroscopic point of view. But at the atomic level, there are no simple, correct expressions for thermal conductivity. Atomically, the thermal conductivity of a system is determined by how atoms comprising the system interact. There are two different approaches for calculating the thermal conductivity of a system.

The first approach employs the Green-Kubo relations. Although this employs analytic expressions which in principle can be solved, in order to calculate the thermal conductivity of a dense fluid or solid using this relation requires the use of molecular dynamics computer simulation.

The second approach is based upon the relaxation time approach. Due to the anharmonicity within the crystal potential, the phonons in the system are known to scatter. There are three main mechanisms for scattering:

  • Boundary scattering, a phonon hitting the boundary of a system;
  • Mass defect scattering, a phonon hitting an impurity within the system and scattering;
  • Phonon-phonon scattering, a phonon breaking into two lower energy phonons or a phonon colliding with another phonon and merging into one higher energy phonon.

[edit] See also

[edit] References

  1. ^ "Heat Exchangers of polypropylene". http://www.segerfrojd.se/ppvsmetal.htm.  081222 segerfrojd.se
  2. ^ Definition of k value from Plastics New Zealand
  • Callister, William (2003). "Appendix B". Materials Science and Engineering - An Introduction. John Wiley & Sons, INC. pp. 757. ISBN 0-471-22471-5. 
  • Halliday, David; Resnick, Robert; & Walker, Jearl(1997). Fundamentals of Physics (5th ed.). John Wiley and Sons, INC., NY ISBN 0-471-10558-9.
  • P A Hilton Ltd., "Thermal Conductivity of Liquids and Gases Unit." P A Hilton. <http://www.p-a-hilton.co.uk/H471.pdf>
  • Srivastava G. P (1990), "The Physics of Phonons." Adam Hilger, IOP Publishing Ltd, Bristol.
  • TM 5-852-6 AFR 88-19, Volume 6 (Army Corp of Engineers publication)

[edit] External links

Retrieved from "http://en.wikipedia.org/wiki/Thermal_conductivity"
Personal tools