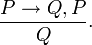Modus ponens
From Wikipedia, the free encyclopedia
In classical logic, modus ponendo ponens (Latin for mode that affirms by affirming;[1] often abbreviated to MP or modus ponens) is a valid, simple argument form sometimes referred to as affirming the antecedent or the law of detachment. It is closely related to another valid form of argument, modus tollens or "denying the consequent".
Modus ponens is a very common rule of inference, and takes the following form:
- If P, then Q.
- P.
- Therefore, Q.[2]
Contents |
[edit] Formal notation
The modus ponens rule may be written in sequent notation:
or in rule form:
[edit] Explanation
The argument form has two premises. The first premise is the "if–then" or conditional claim, namely that P implies Q. The second premise is that P, the antecedent of the conditional claim, is true. From these two premises it can be logically concluded that Q, the consequent of the conditional claim, must be true as well. In Artificial Intelligence, modus ponens is often called forward chaining.
An example of an argument that fits the form modus ponens:
- If today is Tuesday, then I will go to work.
- Today is Tuesday.
- Therefore, I will go to work.
This argument is valid, but this has no bearing on whether any of the statements in the argument are true; the validity of modus ponens means that the conclusion must be true if all the premises are true. An argument can be valid but nonetheless unsound if one or more premises are false; if an argument is valid and all the premises are true, then the argument is sound. A propositional argument using modus ponens is said to be deductive.
In metalogics, modus ponens is the cut rule. The cut-elimination theorem says that the cut is valid (an admissible rule) in some logical calculus (sequent calculus).
[edit] Justification via truth table
The validity of modus ponens in classical two-valued logic can be clearly demonstrated by use of a truth table.
| p | q | p → q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
In instances of modus ponens we assume as premises that p → q is true and p is true. Only one line of the truth table - the first - satisfies these two conditions. On this line, q is also true. Therefore, whenever p → q is true and p is true, q must also be true.
[edit] See also
- Hypothetical syllogism
- Modus tollens
- Modus tollendo ponens
- Affirming the consequent
- Denying the antecedent
- Disjunctive syllogism
- Inference rule
[edit] References
- ^ Stone, Jon R. (1996). Latin for the Illiterati: Exorcizing the Ghosts of a Dead Language. London, UK: Routledge: 60..
- ^ Jago, Mark (2007). Formal Logic. Humanities-Ebooks LLP. ISBN 978-1-84760-041-7.
[edit] External links
- Modus ponens at Wolfram MathWorld