Simpson's paradox

From Wikipedia, the free encyclopedia

Jump to: navigation, search
Simpson's paradox for continuous data: a positive trend appears for two separate groups (blue and red), a negative trend (black, dashed) appears when the data are combined.

Simpson's paradox (or the Yule-Simpson effect) is a statistical paradox wherein the successes of groups seem reversed when the groups are combined. This result is often encountered in social and medical science statistics,[1] and occurs when frequency data are hastily given causal interpretation;[2] the paradox disappears when causal relations are derived systematically, through formal analysis.

Though mostly unknown to laymen, Simpson's Paradox is well known to statisticians, and is described in several introductory statistics books.[3][4] Many statisticians believe that the mainstream public should be apprised of counterintuitive results such as Simpson's paradox,[5] in particular to caution against the inference of causal relationships based on the association between two variables.[6]

Edward H. Simpson described the phenomenon in 1951,[7] along with Karl Pearson et al.,[8] and Udny Yule in 1903.[9] The name Simpson's paradox was coined by Colin R. Blyth in 1972.[10] Since Simpson did not discover this statistical paradox, some authors, instead, have used the impersonal names reversal paradox and amalgamation paradox in referring to what is now called Simpson's Paradox and the Yule-Simpson effect.[11]

Contents

[edit] Examples

[edit] Batting averages

A common example of the paradox involves batting averages in baseball: it is possible for one player to hit for a higher batting average than another player during a given year, and to do so again during the next year, but to have a lower batting average when the two years are combined. This phenomenon, which occurs when there are large differences in the number of at-bats between years, is well-known among sports sabermetricians such as Bill James.

A real-life example is provided by Ken Ross[12] and involves the batting average of baseball players Derek Jeter and David Justice during the years 1995 and 1996:[13]

1995 1996 Combined
Derek Jeter 12/48 .250 183/582 .314 195/630 .310
David Justice 104/411 .253 45/140 .321 149/551 .270

In both 1995 and 1996, Justice had a higher batting average (in bold) than Jeter; however, when the two years are combined, Jeter shows a higher batting average than Justice. According to Ross, this phenomenon would be observed about once per year among the interesting baseball players. In this particular case, the paradox can still be observed if the year 1997 is also taken into account:

1995 1996 1997 Combined
Derek Jeter 12/48 .250 183/582 .314 190/654 .291 385/1284 .300
David Justice 104/411 .253 45/140 .321 163/495 .329 312/1046 .298

The Jeter/Justice example of Simpson's Paradox was referred to in the "Conspiracy Theory" episode of Numb3rs; although a chart in the show omitted some of the data and listed the 1996 averages as occurring in 1995.

[edit] Kidney stone treatment

This is a real-life example from a medical study[14] comparing the success rates of two treatments for kidney stones.[15]

The first table shows the overall success rates and numbers of treatments for both treatments (where Treatment A includes all open procedures and Treatment B is percutaneous nephrolithotomy):

Treatment A Treatment B
78% (273/350) 83% (289/350)

This seems to show treatment B is more effective. If we include data about kidney stone size, however, the same set of treatments reveals a different answer:

Treatment A Treatment B
Small Stones Group 1
93% (81/87)		 Group 2
87% (234/270)
Large Stones Group 3
73% (192/263)		 Group 4
69% (55/80)
Both 78% (273/350) 83% (289/350)

The information about stone size has reversed our conclusion about the effectiveness of each treatment. Now treatment A is seen to be more effective in both cases. In this example the lurking variable (or confounding variable) of stone size was not previously known to be important until its effects were included.

Which treatment is considered better is determined by an inequality between two ratios (successes/total). The reversal of the inequality between the ratios, which creates Simpson's paradox, happens because two effects occur together:

  1. The sizes of the groups, which are combined when the lurking variable is ignored, are very different. Doctors tend to give the severe cases (large stones) the better treatment (A), and the milder cases (small stones) the inferior treatment (B). Therefore, the totals are dominated by groups 3 and 2, and not by the two much smaller groups 1 and 4.
  2. The lurking variable has a large effect on the ratios, i.e. the success rate is more strongly influenced by the severity of the case than by the choice of treatment. Therefore, the group of patients with large stones using treatment A (group 3) does worse than the group with small stones, even if the latter used the inferior treatment B (group 2).

[edit] Berkeley sex bias case

One of the best known real life examples of Simpson's paradox occurred when the University of California, Berkeley was sued for bias against women applying to graduate school. The admission figures for fall 1973 showed that men applying were more likely than women to be admitted, and the difference was so large that it was unlikely to be due to chance.[16][3]

Applicants  % admitted
Men 8442 44%
Women 4321 35%

However when examining the individual departments, it was found that no department was significantly biased against women; in fact, most departments had a small bias against men.

Major Men Women
Applicants  % admitted Applicants  % admitted
A 825 62% 108 82%
B 560 63% 25 68%
C 325 37% 593 34%
D 417 33% 375 35%
E 191 28% 393 24%
F 272 6% 341 7%

The explanation turned out to be that women tended to apply to competitive departments with low rates of admission even among qualified applicants (such as English), while men tended to apply to less-competitive departments with high rates of admission among qualified applicants (such as engineering). The conditions under which department-specific frequency data constitute a proper defense against charges of discrimination are formulated in Pearl (2000).

[edit] 2006 US school study

In July 2006, the United States Department of Education released a study[17] documenting student performances in reading and math in different school settings.[18] It reported that while the math and reading levels for students at grades 4 and 8 were uniformly higher in private/parochial schools than in public schools, repeating the comparisons on demographic subgroups showed much smaller differences, which were nearly equally divided in direction.

[edit] Low birth weight paradox

Main article: Low birth weight paradox

The low birth weight paradox is an apparently paradoxical observation relating to the birth weights and mortality of children born to tobacco smoking mothers. Traditionally, babies weighing less than a certain amount (which varies between countries) have been classified as having low birth weight. In a given population, low birth weight babies have a significantly higher mortality rate than others. However, it has been observed that low birth weight children born to smoking mothers have a lower mortality rate than the low birth weight children of non-smokers.[19]

[edit] Description

Illustration of Simpson's Paradox; The first graph represents Lisa's contribution, the second one Bart's. The red bars represent the first week, the blue bars the second week; the triangles indicate the combined percentage of good contributions (weighted average). While Bart's bars both show a higher rate of success than Lisa's, Lisa's combined rate is higher because basically she improved a greater ratio relative to the quantity edited.

Suppose two people, Lisa and Bart, each edit Wikipedia articles for two weeks. In the first week, Lisa improves 60 percent of the 100 articles she edited, and Bart improves 90 percent of 10 articles he edited. In the second week, Lisa improves just 10 percent of 10 articles she edited, while Bart improves 30 percent of 100 articles he edited.

Week 1 Week 2 Total
Lisa 60/100 1/10 61/110
Bart 9/10 30/100 39/110

Both times Bart improved a higher percentage of articles than Lisa, but the actual number of articles each edited (the bottom number of their ratios also known as the sample size) were not the same for both of them either week. When the totals for the two weeks are added together, Bart and Lisa's work can be judged from an equal sample size, i.e. the same number of articles edited by each. Looked at in this more accurate manner, Lisa's ratio is higher and, therefore, so is her percentage. Also when the two tests are combined using a weighted average, overall, Lisa has improved a much higher percentage than Bart because the quality modifier had a significantly higher percentage. Therefore, like other paradoxes, it only appears to be a paradox because of incorrect assumptions, incomplete or misguided information, or a lack of understanding a particular concept.

Week 1 quantity percentage Week 2 quantity percentage Total quantity and weighted quality percentage
Lisa 60% 10% 55.5%
Bart 90% 30% 35.5%

This imagined paradox is caused when the percentage is provided but not the ratio. In this example, if only the 90% in the first week for Bart was provided but not the ratio (9:10), it would distort the information causing the imagined paradox. Even though Bart's percentage is higher for the first and second week, when two week's of articles is combined, overall Lisa had improved a greater proportion, 55% of the 110 total articles. Lisa's proportional total of articles improved exceeds Bart's total.

Here are some notations:

  • In the first week
  • S_L(1) = 60\% — Lisa improved 60% of the many articles she edited.
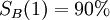  • S_B(1) = 90\% — Bart had a 90% success rate during that time.
Success is associated with Bart.
  • In the second week
  • S_L(2) = 10\% — Lisa managed 10% in her busy life.
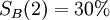  • S_B(2) = 30\% — Bart achieved a 30% success rate.
Success is associated with Bart.

On both occasions Bart's edits were more successful than Lisa's. But if we combine the two sets, we see that Lisa and Bart both edited 110 articles, and:

  • S_L = \begin{matrix}\frac{61}{110}\end{matrix} — Lisa improved 61 articles.
  • S_B = \begin{matrix}\frac{39}{110}\end{matrix} — Bart improved only 39.
  • S_L > S_B \, — Success is now associated with Lisa.

Bart is better for each set but worse overall.

The paradox stems from our healthy intuition that Bart could not possibly be a better editor on each set but worse overall. Pearl (2000) in fact proved the impossibility of such happening, where "better editor" is taken in the counterfactual sense: "Were Bart to edit all items in a set he would do better than Lisa would, on those same items." Clearly, frequency data cannot support this sense of "better editor," because it does not tell us how Bart would perform on items edited by Lisa, and vice versa. In the back of our mind, though, we assume that the articles were assigned at random to Bart and Lisa, an assumption which (for large sample) would support the counterfactual interpretation of "better editor." However, under random assignment conditions, the data given in this example is impossible, which accounts for our surprise when confronting the rate reversal.

The arithmetical basis of the paradox is uncontroversial. If SB(1) > SL(1) and SB(2) > SL(2) we feel that SB must be greater than SL. However if different weights are used to form the overall score for each person then this feeling may be disappointed. Here the first test is weighted \begin{matrix}\frac{100}{110}\end{matrix} for Lisa and \begin{matrix}\frac{10}{110}\end{matrix} for Bart while the weights are reversed on the second test.

  • S_L = \begin{matrix}\frac{100}{110}\end{matrix}S_L(1) + \begin{matrix}\frac{10}{110}\end{matrix}S_L(2)
  • S_B = \begin{matrix}\frac{10}{110}\end{matrix}S_B(1) + \begin{matrix}\frac{100}{110}\end{matrix}S_B(2)

By more extreme reweighting Lisa's overall score can be pushed up towards 60% and Bart's down towards 30%.

Lisa is a better editor on average, as her overall success rate is higher. But it is possible to have told the story in a way which would make it appear obvious that Bart is more diligent.

Simpson's paradox shows us an extreme example of the importance of including data about possible confounding variables when attempting to calculate causal relations. Precise criteria for selecting a set of "confounding variables," (i.e., variables that yield correct causal relationships if included in the analysis), is given in (Pearl, 2000) using causal graphs.

While Simpson's paradox often refers to the analysis of count tables, as shown in this example, it also occurs with continuous data:[20] for example, if one fits separated regression lines through two sets of data, the two regression lines may show a positive trend, while a regression line fitted through all data together will show a negative trend, as shown on the picture above.

[edit] Vector interpretation

Vector interpretation of Simpson's paradox (note that the x and y axes have different scales).

Simpson's paradox can also be illustrated using the 2-dimensional vector space.[21] A success rate of p / q can be represented by a vector \overrightarrow{A}=(q,p), with a slope of p / q. 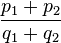If two rates p1 / q1 and p2 / q2 are combined, as in the examples given above, the result can be represented by the sum of the vectors (q1,p1) and (q2,p2), which according to the parallelogram rule is the vector (q1 + q2,p1 + p2), with slope \frac{p_1+p_2}{q_1+q_2}.

Simpson's paradox says that even if a vector \overrightarrow{b_1} (in blue in the figure) has a smaller slope than another vector \overrightarrow{r_1} (in red), and \overrightarrow{b_2} has a smaller slope than \overrightarrow{r_2}, the sum of the two vectors \overrightarrow{b_1} + \overrightarrow{b_2} (indicated by "+" in the figure) can still have a larger slope than the sum of the two vectors \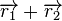overrightarrow{r_1} + \overrightarrow{r_2}, as shown in the example.

[edit] References

  1. ^ Clifford H. Wagner (February 1982). "Simpson's Paradox in Real Life". The American Statistician 36 (1): 46–48. doi:10.2307/2684093. 
  2. ^ Judea Pearl. Causality: Models, Reasoning, and Inference, Cambridge University Press, 2000. ISBN 0-521-77362-8.
  3. ^ a b David Freedman, Robert Pisani and Roger Purves. Statistics (3rd edition). W.W. Norton, 1998, p. 19. ISBN 0-393-97083-3.
  4. ^ David S. Moore and D.S. George P. McCabe (February 2005). "Introduction to the Practice of Statistics" (5th edition). W.H. Freeman & Company. ISBN 071676282X.
  5. ^ Robert L. Wardrop (February 1995). "Simpson's Paradox and the Hot Hand in Basketball". The American Statistician, 49 (1): pp. 24–28.
  6. ^ Alan Agresti (2002). "Categorical Data Analysis" (Second edition). John Wiley and Sons. ISBN 0-471-36093-7
  7. ^ Simpson, Edward H. (1951). "The Interpretation of Interaction in Contingency Tables". Journal of the Royal Statistical Society, Ser. B 13: 238–241. 
  8. ^ Pearson, Karl; Lee, A.; Bramley-Moore, L. (1899), "Genetic (reproductive) selection: Inheritance of fertility in man", Philosophical Translations of the Royal Statistical Society, Ser. A 173: 534–539 
  9. ^ G. U. Yule (1903). "Notes on the Theory of Association of Attributes in Statistics". Biometrika 2: 121–134. doi:10.1093/biomet/2.2.121. 
  10. ^ Colin R. Blyth (June 1972). "On Simpson's Paradox and the Sure-Thing Principle". Journal of the American Statistical Association 67 (338): 364–366. doi:10.2307/2284382. 
  11. ^ I. J. Good, Y. Mittal (June 1987). "The Amalgamation and Geometry of Two-by-Two Contingency Tables". The Annals of Statistics 15 (2): 694–711. doi:10.1214/aos/1176350369. 
  12. ^ Ken Ross. "A Mathematician at the Ballpark: Odds and Probabilities for Baseball Fans (Paperback)" Pi Press, 2004. ISBN 0131479903. 12–13
  13. ^ Statistics available from http://www.baseball-reference.com/ : Data for Derek Jeter, Data for David Justice.
  14. ^ C. R. Charig, D. R. Webb, S. R. Payne, O. E. Wickham (1986 March 29). "Comparison of treatment of renal calculi by operative surgery, percutaneous nephrolithotomy, and extracorporeal shock wave lithotripsy". Br Med J (Clin Res Ed) 292 (6524): 879–882. PMID 3083922. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pubmed&pubmedid=3083922. 
  15. ^ Steven A. Julious and Mark A. Mullee (12/03/1994). "Confounding and Simpson's paradox". BMJ 309 (6967): 1480–1481. PMID 7804052. http://bmj.bmjjournals.com/cgi/content/full/309/6967/1480. 
  16. ^ P.J. Bickel, E.A. Hammel and J.W. O'Connell (1975). "Sex Bias in Graduate Admissions: Data From Berkeley". Science 187 (4175): 398–404. doi:10.1126/science.187.4175.398. PMID 17835295. .
  17. ^ H. Braun, F. Jenkins and W. Grigg, (2006) "Comparing Private Schools and Public Schools Using Hierarchical Linear Modeling, U.S. Department of Education, National Center for Education Statistics, Institute of Education Sciences, Washington, DC, United States Government Printing Office.
  18. ^ Diana Jean Schemo. "Public Schools Perform Near Private Ones in Study. The New York Times, 15 July 2006. Retrieved on 25 July 2007.
  19. ^ Wilcox, Allen (2006). "The Perils of Birth Weight — A Lesson from Directed Acyclic Graphs". American Journal of Epidemiology. 164(11):1121–1123.
  20. ^ John Fox (1997). "Applied Regression Analysis, Linear Models, and Related Methods". Sage Publications. ISBN 080394540X. 136–137
  21. ^ Jerzy Kocik (December 2001). Proofs without Words: Simpson's Paradox. Mathematics Magazine. 74 (5), p. 399.

[edit] External links

For a brief history of the origins of the paradox see the entries "Simpson's Paradox and Spurious Correlation" in

Retrieved from "http://en.wikipedia.org/wiki/Simpson%27s_paradox"
Personal tools