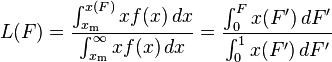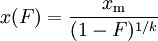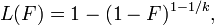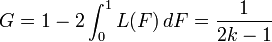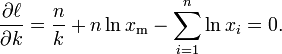Pareto distribution

From Wikipedia, the free encyclopedia

Jump to: navigation, search
Pareto
Probability density function
Pareto probability density functions for various k
Pareto probability density functions for various k  with xm = 1. The horizontal axis is the x  parameter. As k → ∞ the distribution approaches δ(x − xm) where δ is the Dirac delta function.
Cumulative distribution function
Pareto cumulative distribution functions for various k
Pareto cumulative distribution functions for various k  with xm = 1. The horizontal axis is the x  parameter.
Parameters x_\mathrm{m}>0\, scale (real)
k>0\, shape (real)
Support x \in [x_\mathrm{m}; +\infty)\!
Probability density function (pdf) \frac{k\,x_\mathrm{m}^k}{x^{k+1}}\!
Cumulative distribution function (cdf) 1-\left(\frac{x_\mathrm{m}}{x}\right)^k\!
Mean \frac{k\,x_\mathrm{m}}{k-1}\! for k > 1
Median x_\mathrm{m} \sqrt[k]{2}
Mode x_\mathrm{m}\,
Variance \frac{x_\mathrm{m}^2k}{(k-1)^2(k-2)}\! for k > 2
Skewness \frac{2(1+k)}{k-3}\,\sqrt{\frac{k-2}{k}}\! for k > 3
Excess kurtosis \frac{6(k^3+k^2-6k-2)}{k(k-3)(k-4)}\! for k > 4
Entropy \ln\left(\frac{k}{x_\mathrm{m}}\right) - \frac{1}{k} - 1\!
Moment-generating function (mgf) undefined; see text for raw moments
Characteristic function k(-ix_\mathrm{m}t)^k\Gamma(-k,-ix_\mathrm{m}t)\,

The Pareto distribution, named after the Italian economist Vilfredo Pareto, is a power law probability distribution that coincides with social, scientific, geophysical, actuarial, and many other types of observable phenomena. Outside the field of economics it is at times referred to as the Bradford distribution.

Pareto originally used this distribution to describe the allocation of wealth among individuals since it seemed to show rather well the way that a larger portion of the wealth of any society is owned by a smaller percentage of the people in that society. This idea is sometimes expressed more simply as the Pareto principle or the "80-20 rule" which says that 20% of the population controls 80% of the wealth[1]. It can be seen from the probability density function (PDF) graph on the right, that the "probability" or fraction of the population that owns a small amount of wealth per person is rather high, and then decreases steadily as wealth increases. This distribution is not limited to describing wealth or income distribution, but to many situations in which an equilibrium is found in the distribution of the "small" to the "large". The following examples are sometimes seen as approximately Pareto-distributed:

  • The sizes of human settlements (few cities, many hamlets/villages)
  • File size distribution of Internet traffic which uses the TCP protocol (many smaller files, few larger ones)
  • Clusters of Bose-Einstein condensate near absolute zero
  • The values of oil reserves in oil fields (a few large fields, many small fields)
  • The length distribution in jobs assigned supercomputers (a few large ones, many small ones)
  • The standardized price returns on individual stocks
  • Sizes of sand particles
  • Sizes of meteorites
  • Numbers of species per genus (There is subjectivity involved: The tendency to divide a genus into two or more increases with the number of species in it)
  • Areas burnt in forest fires
  • Severity of large casualty losses for certain lines of business such as general liability, commercial auto, and workers compensation.

Contents

[edit] Properties

[edit] Definition

If X is a random variable with a Pareto distribution, then the probability that X is greater than some number x is given by

\Pr(X>x)=\left(\frac{x}{x_\mathrm{m}}\right)^{-k}

for all x ≥ xm, where xm is the (necessarily positive) minimum possible value of X, and k is a positive parameter. The family of Pareto distributions is parameterized by two quantities, xm and k. When this distribution is used to model the distribution of wealth, then the parameter k is called the Pareto index.

It follows from the above that therefore the cumulative distribution function of a Pareto random variable with parameters k and xm is

F_X(x)=1-\left(\frac{x}{x_\mathrm{m}}\right)^{-k}

[edit] Density function

It follows (by differentiation) that the probability density function is

f(x;k,x_\mathrm{m})= k\,\frac{x_\mathrm{m}^k}{x^{k+1}}\ \mbox{for}\ x \ge x_\mathrm{m}. \,

[edit] Various properties

The expected value of a random variable following a Pareto distribution is

E(X)=\frac{kx_\mathrm{m}}{k-1} \,

(if k ≤ 1, the expected value is infinite). Its variance is

\mathrm{var}(X)=\left(\frac{x_\mathrm{m}}{k-1}\right)^2 \frac{k}{k-2}.

(If k \le 2, the variance is infinite). The raw moments are found to be

\mu_n'=\frac{kx_\mathrm{m}^n}{k-n}, \,

but they are only defined for k > n. This means that the moment generating function, which is just a Taylor series in x with μn' / n! as coefficients, is not defined. The characteristic function is given by

\varphi(t;k,x_\mathrm{m})=k(-ix_\mathrm{m} t)^k\Gamma(-k,-ix_\mathrm{m} t),

where Γ(a,x) is the incomplete gamma function. The Pareto distribution is related to the exponential distribution by

f(x;k,x_\mathrm{m})=\mathrm{Exponential}(\ln(x/x_\mathrm{m});k).\,

The Dirac delta function is a limiting case of the Pareto distribution:

\lim_{k\rightarrow \infty} f(x;k,x_\mathrm{m})=\delta(x-x_\mathrm{m}). \,

[edit] A characterization theorem

Suppose Xi, i = 1, 2, 3, ... are independent identically distributed random variables whose probability distribution is supported on the interval [k, ∞) for some k > 0. Suppose that for all n, the two random variables min{ X1, ..., Xn } and (X1 + ... + Xn)/min{ X1, ..., Xn } are independent. Then the common distribution is a Pareto distribution.

[edit] Relation to Zipf's law

Pareto distributions are continuous probability distributions. Zipf's law, also sometimes called the zeta distribution, may be thought of as a discrete counterpart of the Pareto distribution.

[edit] Pareto, Lorenz, and Gini

Lorenz curves for a number of Pareto distributions. The k = ∞ corresponds to perfectly equal distribution (G = 0) and the k = 1 line corresponds to complete inequality (G = 1)

The Lorenz curve is often used to characterize income and wealth distributions. For any distribution, the Lorenz curve L(F) is written in terms of the PDF ƒ or the CDF F as

L(F)=\frac{\int_{x_\mathrm{m}}^{x(F)} xf(x)\,dx}{\int_{x_\mathrm{m}}^\infty xf(x)\,dx} =\frac{\int_0^F x(F')\,dF'}{\int_0^1 x(F')\,dF'}

where x(F) is the inverse of the CDF. For the Pareto distribution,

x(F)=\frac{x_\mathrm{m}}{(1-F)^{1/k}}

and the Lorenz curve is calculated to be

L(F) = 1-(1-F)^{1-1/k},\,

where k must be greater than or equal to unity, since the denominator in the expression for L(F) is just the mean value of x. Examples of the Lorenz curve for a number of Pareto distributions are shown in the graph on the right.

The Gini coefficient is a measure of the deviation of the Lorenz curve from the equidistribution line which is a line connecting [0, 0] and [1, 1], which is shown in black (k = ∞) in the Lorenz plot on the right. Specifically, the Gini coefficient is twice the area between the Lorenz curve and the equidistribution line. The Gini coefficient for the Pareto distribution is then calculated to be

G = 1-2\int_0^1L(F)\,dF = \frac{1}{2k-1}

(see Aaberge 2005).

[edit] Parameter estimation

The likelihood function for the Pareto distribution parameters k and xm, given a sample x = (x_1, x_2, \dots, x_n), is

L(k, x_\mathrm{m}) = \prod _{i=1} ^n {k \frac {x_\mathrm{m}^k} {x_i^{k+1}}} = k^n x_\mathrm{m}^{nk} \prod _{i=1} ^n {\frac 1 {x_i^{k+1}}}. \!

Therefore, the logarithmic likelihood function is

\ell(k, x_\mathrm{m}) = n \ln k + nk \ln x_\mathrm{m} - (k + 1) \sum _{i=1} ^n {\ln x_i}. \!

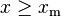It can be seen that \ell(k, x_\mathrm{m}) is monotonically increasing with xm, that is, the greater the value of xm, the greater the value of the likelihood function. Hence, since x \ge x_\mathrm{m}, we conclude that

\widehat x_\mathrm{m} = \min _i {x_i}.

To find the estimator for k, we compute the corresponding partial derivative and determine where it is zero:

\frac{\partial \ell}{\partial k} = \frac{n}{k} + n \ln x_\mathrm{m} - \sum _{i=1} ^n {\ln x_i} = 0.

Thus the maximum likelihood estimator for k is:

\widehat k = \frac n {\sum _i {\left( \ln x_i - \ln \widehat x_\mathrm{m} \right)}}.

The expected statistical error is:

\sigma = \frac {\widehat k} {\sqrt n}. [1]

[edit] Graphical representation

The characteristic curved 'long tail' distribution when plotted on a linear scale, masks the underlying simplicity of the function when plotted on a log-log graph, which then takes the form of a straight line with negative gradient.

[edit] Generating a random sample from Pareto distribution

The Pareto distribution is not yet recognized by many programming languages. In the actuarial field, the Pareto distribution is widely used to estimate portfolio costs. As a matter of fact, it can be quite demanding to get data from this particular probability distribution. One can easily generate a random sample from Pareto distribution by mixing two random variables, which are usually built-in many statistical tools. The process is quite simple; one has to generate numbers from an exponential distribution with its λ equal to a random generated sample from a gamma distribution

\displaystyle k_\mathrm{Gamma}=k_\mathrm{Pareto}\,

and

\theta_\mathrm{Gamma}=\frac1{x_{\mathrm{m}_\mathrm{Pareto}}}.

This process generates data starting at 0, so then we need to add xm.

Alternatively, random samples can be generated using inverse transform sampling. Given a random variate U drawn from the uniform distribution on the unit interval (0;1), the variate

T=\frac{x_\mathrm{m}}{U^{1/k}}

is Pareto-distributed. [2]

[edit] Bounded Pareto distribution

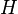The bounded Pareto distribution has three parameters k, L \, and H \,. As in the standard Pareto distribution k determines the shape. L denotes the minimal value, and H denotes the maximal value.

Bounded Pareto
Probability density function
Cumulative distribution function
Parameters L > 0 \, location (real)

H > L \, location (real)
k > 0 \, shape (real)
Support L \leqslant x \leqslant H \,
Probability density function (pdf) \frac{k L^k x^{-k - 1}}{1-\left(\frac{L}{H}\right)^k}
Cumulative distribution function (cdf)
Mean \frac{L^k}{1 - \left(\frac{L}{H}\right)^k} \cdot \left(\frac{k}{k-1}\right) \cdot \left(\frac{1}{L^{k-1}} - \frac{1}{H^{k-1}}\right) \; k > 1
Median
Mode
Variance \frac{L^k}{1 - \left(\frac{L}{H}\right)^k} \cdot \left(\frac{k}{k-2}\right) \cdot \left(\frac{1}{L^{k-2}} - \frac{1}{H^{k-2}}\right) \; k > 2
Skewness
Excess kurtosis
Entropy
Moment-generating function (mgf)
Characteristic function

The probability density function is

\frac{k L^k x^{-k - 1}}{1-\left(\frac{L}{H}\right)^k}

where L \leqslant x \leqslant H, and k > 0.

[edit] Generating bounded Pareto random variables

If U is uniformly distributed on (0, 1), then

\left(\frac{U H^k - U L^k - H^k}{H^k L^k}\right)^{-1/k}

is bounded Pareto-distributed [3]

[edit] Generalized Pareto distribution

The family of generalized Pareto distributions (GPD) has three parameters \mu,\sigma \, and \xi \,.

Generalized Pareto
Probability density function
Cumulative distribution function
Parameters \mu \in (-\infty,\infty) \, location (real)

\sigma \in (0,\infty) \, scale (real)
\xi\in (-\infty,\infty) \, shape (real)
Support x \geqslant \mu\,\;(\xi \geqslant 0)

\mu \leqslant x \leqslant \mu-\sigma/\xi\,\;(\xi < 0)
Probability density function (pdf) \frac{1}{\sigma}(1 + \xi z )^{-(1/\xi +1)}

where z=\frac{x-\mu}{\sigma}
Cumulative distribution function (cdf) 1-(1+\xi z)^{-1/\xi} \,
Mean \mu + \frac{\sigma}{1-\xi}\, \; (\xi < 1)
Median \mu + \frac{\sigma( 2^{\xi} -1)}{\xi}
Mode
Variance \frac{\sigma^2}{(1-\xi)^2(1-2\xi)}\, \; (\xi < 1/2)
Skewness
Excess kurtosis
Entropy
Moment-generating function (mgf)
Characteristic function

The cumulative distribution function is

F_{(\xi,\mu,\sigma)}(x) = 1 - \left(1+ \frac{\xi(x-\mu)}{\sigma}\right)^{-1/\xi}

for x \geqslant \mu , and x \leqslant \mu - \sigma /\xi when \xi < 0 \, , where \mu\in\mathbb R is the location parameter, \sigma>0 \, the scale parameter and \xi\in\mathbb R the shape parameter. Note that some references give the "shape parameter" as \kappa = - \xi \,.

The probability density function is

f_{(\xi,\mu,\sigma)}(x) = \frac{1}{\sigma}\left(1 + \frac{\xi (x-\mu)}{\sigma}\right)^{\left(-\frac{1}{\xi} - 1\right)}.

again, for x \geqslant \mu , and x \leqslant \mu - \sigma /\xi when \xi < 0 \, .

[edit] Generating generalized Pareto random variables

If U is uniformly distributed on (0, 1], then

X = \mu + \frac{\sigma (U^{-\xi}-1)}{\xi} \sim \mbox{GPD}(\mu,\sigma,\xi).
This section requires expansion.

[edit] Annotations

  1. ^ For a two-quantile population, where 18% of the population owns 82% of the wealth, the Theil index takes the value 1.

[edit] References

  • Lorenz, M. O. (1905). Methods of measuring the concentration of wealth. Publications of the American Statistical Association. 9: 209–219.

[edit] See also

[edit] External links

v • d • e
Probability distributions
 
Continuous univariate supported on a semi-infinite interval, usually [0,∞)
Retrieved from "http://en.wikipedia.org/wiki/Pareto_distribution"
Personal tools