Pythagorean tuning
From Wikipedia, the free encyclopedia
Pythagorean tuning is a system of musical tuning in which the frequency relationships of all intervals are based on the ratio 3:2. Its name comes from medieval texts which attribute its discovery to Pythagoras, but its use has been documented as long ago as 3500 B.C. in Babylonian texts.[1] It is the oldest way of tuning the 12-note chromatic scale.
![]() play diatonic scale in Pythagorean tuning (help·info)
play diatonic scale in Pythagorean tuning (help·info) ![]() contrast with diatonic scale in 12-et (help·info)
contrast with diatonic scale in 12-et (help·info) ![]() contrast with just diatonic scale (help·info)
contrast with just diatonic scale (help·info)
Contents |
[edit] Method
Pythagorean tuning is based on a stack of perfect fifths, each tuned in the ratio 3:2, the next simplest ratio after 2:1, which is the ratio of an octave. Starting from D for example, the A is tuned such that the frequency ratio of A and D is 3:2 — if D is tuned to 288 Hz, then the A is tuned to 432 Hz. The E above A is also tuned in the ratio 3:2 — with the A at 432 Hz, this puts the E at 648 Hz, 9:4 above the original D. When describing tunings, it is usual to speak of all notes as being within an octave of each other, and as this E is over an octave above the original D, it is usual to halve its frequency to move it down an octave. Therefore, the E is tuned to 324 Hz, a 9:8 above the D. The B at 3:2 above that E is tuned to the ratio 27:16 and so on. Starting from the same point working the other way, also from D to G is tuned as 3:2. With D at 288 Hz, this arrives at G at 192 Hz, or, brought into the same octave, to 384 Hz.
In applying this tuning to the chromatic scale, however, a problem arises: no number of 3:2s will fit exactly into an octave. Because of this, the G♯, separated by twelve fifths from the A♭, is about a quarter of a semitone sharper. The table below illustrates this, showing the note and interval name, the ratio above D, and the value in cents above the D for each note in the equally tempered scale and the difference between the Pythagorean and Equally tempered scale.
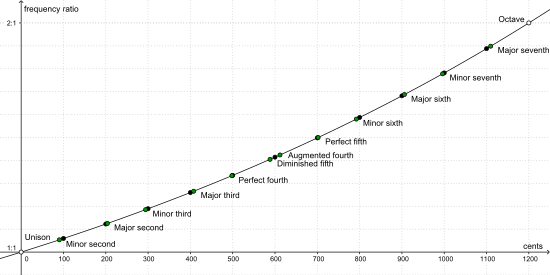
| Ratio | Note | Interval | ET | ET-dif |
| cents | ||||
| 1024:729 | A♭ | diminished fifth | 588.27 | -11.73 |
| 256:243 | E♭ | minor second | 90.22 | -9.78 |
| 128:81 | B♭ | minor sixth | 792.18 | -7.82 |
| 32:27 | F | minor third | 294.13 | -5.87 |
| 16:9 | C | minor seventh | 996.09 | -3.91 |
| 4:3 | G | perfect fourth | 498.04 | -1.96 |
| 1:1 | D | unison | 0 .00 | 0.00 |
| 3:2 | A | perfect fifth | 701.96 | 1.96 |
| 9:8 | E | major second | 203.91 | 3.91 |
| 27:16 | B | major sixth | 905.87 | 5.87 |
| 81:64 | F♯ | major third | 407.82 | 7.82 |
| 243:128 | C♯ | major seventh | 1109.78 | 9.78 |
| 729:512 | G♯ | augmented fourth | 611.73 | 11.73 |
The major scale based on C, obtained from this tuning is:
| Note | C | D | E | F | G | A | B | C | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ratio | 1/1 | 9/8 | 81/64 | 4/3 | 3/2 | 27/16 | 243/128 | 2/1 | ||||||||
| Step | 9/8 | 9/8 | 256/243 | 9/8 | 9/8 | 9/8 | 256/243 | |||||||||
In equal temperament, pairs of enharmonic notes such as A flat and G sharp are thought of as being the same note — however, as the above table indicates, in Pythagorean tuning, they theoretically have different ratios, and are at a different frequency. This discrepancy, of about 23.5 cents, or one quarter of a semitone, is known as a Pythagorean comma.
To get around this problem, Pythagorean tuning uses the above 12 notes from A flat to G sharp shown above, and then places above the G sharp another A flat, starting the sequence again. This leaves that interval badly out-of-tune, meaning that any music which combines those two notes is unplayable in this tuning. A very out-of-tune interval such as this one is known as a wolf interval. In the case of Pythagorean tuning, all the fifths are 701.96 cents wide, in the exact ratio 3:2, except the wolf fifth, which is only 678.49 cents wide, nearly a quarter of a semitone flatter.
If the notes D♯ and E♭ need to be sounded together, the position of the wolf fifth can be changed (for example, the above table could run from A to E, making that the wolf interval instead of E♭ to D♯). However, there will always be one wolf fifth in Pythagorean tuning, making it impossible to play in all keys in tune.
Because of the wolf interval, this tuning is rarely used nowadays, although it is thought to have been widespread. In music which does not change key very often, or which is not very harmonically adventurous, the wolf interval is unlikely to be a problem, as not all the possible fifths will be heard in such pieces.
Because fifths in Pythagorean tuning are in the simple ratio of 3:2, they sound very "smooth" and consonant. The thirds, by contrast, which are in the relatively complex ratios of 81:64 (for major thirds) and 32:27 (for minor thirds), sound less smooth. For this reason, Pythagorean tuning is particularly well suited to music which treats fifths as consonances, and thirds as dissonances. In western classical music, this usually means music written prior to the 15th century. As thirds came to be treated as consonances, so meantone temperament, and particularly quarter-comma meantone, which tunes thirds to the relatively simple ratio of 5:4, became more popular. However, meantone still has a wolf interval, so is not suitable for all music.
From around the 18th century, as the need grew for instruments to change key, and therefore to avoid a wolf interval, this led to the widespread use of well temperaments and eventually equal temperament.
[edit] Discography
- Gothic Voices - Music for the Lion-Hearted King (Hyperion, CDA66336, 1989), directed by Christopher Page (Leech-Wilkinson)
- Lou Harrison performed by John Schneider and the Cal Arts Percussion Ensemble conducted by John Bergamo - Guitar & Percussion (Etceter Records, KTC1071, 1990): Suite No. 1 for guitar and percussion and Plaint & Variations on "Song of Palestine"
[edit] See also
- Pythagorean interval
- Enharmonic scale
- Temperament
- Timaeus (dialogue), in which Plato discusses Pythagorean tuning
- List of musical intervals
- Whole-tone scale
- Regular temperament
- List of meantone intervals
[edit] References
[edit] Footnotes
- ^ West, M.L., "The Babylonian Musical Notation and the Hurrian Melodic Texts", Music & Letters, Vol. 75, no. 2., May, 1994, pp. 161-179
[edit] Notations
- Daniel Leech-Wilkinson (1997), "The good, the bad and the boring", Companion to Medieval & Renaissance Music. Oxford University Press. ISBN 0-19-816540-4.
[edit] External links
- "A Pythagorean tuning of the diatonic scale", with audio samples.
- "Pythagorean Tuning and Medieval Polyphony", by Margo Schulter.
|
||||||||||||||||||||||

