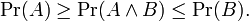Conjunction fallacy
From Wikipedia, the free encyclopedia
The conjunction fallacy is a logical fallacy that occurs when it is assumed that specific conditions are more probable than a single general one.
The most oft-cited example of this fallacy originated with Amos Tversky and Daniel Kahneman:[1]
- Linda is 31 years old, single, outspoken, and very bright. She majored in philosophy. As a student, she was deeply concerned with issues of discrimination and social justice, and also participated in anti-nuclear demonstrations.
- Which is more probable?
- Linda is a bank teller.
- Linda is a bank teller and is active in the feminist movement.
85% of those asked chose option 2.[2] However, mathematically, the probability of two events occurring together (in "conjunction") will always be less than or equal to the probability of either one occurring alone.
In mathematical notation, this inequality could be written for two events A and B as
For example, even choosing a very low probability of Linda being a bank teller, say Pr(Linda is a bank teller) = .05 and a high probability that she would be a feminist, say Pr(Linda is a feminist) = .95, then, assuming independence, Pr(Linda is a bank teller AND Linda is a feminist) = .05 × .95 or .0475, lower than Pr(Linda is a bank teller).
Tversky and Kahneman argue that most people get this problem wrong because they use the representativeness heuristic to make this kind of judgment: Option 2 seems more "representative" of Linda based on the description of her, even though it is clearly mathematically less likely.
(As a side issue, some people may simply be confused by the difference between 'and' and 'or'. Such confusions are often seen in those who have not studied logic, and the probability of such sentences using 'or' instead of 'and' is completely different. They may imply sentence #1 assumes Linda is necessarily not active in the feminist movement.)
Many other demonstrations of this error have been studied. In another experiment, for instance, policy experts were asked to rate the probability that the Soviet Union would invade Poland, and the United States would break off diplomatic relations, all in the following year. They rated it on average as having a 4% probability of occurring. Another group of experts was asked to rate the probability simply that the United States would break off relations with the Soviet Union in the following year. They gave it an average probability of only 1%. Researchers argued that a detailed, specific scenario seemed more likely because of the representativeness heuristic, but each added detail would actually make the scenario less and less likely.[3] In this way it could be similar to the misleading vividness or slippery slope fallacies, though it is possible that people underestimate the general possibility of an event occurring when not given a plausible scenario to ponder.
[edit] Notes
- ^ Tversky & Kahneman (1982, 1983)
- ^ Many variations of this experiment in wording and framing have been published. When Tversky and Kahneman (1983) changed the first option to "Linda is a bank teller whether or not she is active in the feminist movement" in the same experiment as described a majority of respondents still preferred the second option.
- ^ Tversky & Kahneman (1983)
[edit] References
- Tversky, A. and Kahneman, D. (October 1983). "Extension versus intuitive reasoning: The conjunction fallacy in probability judgment". Psychological Review 90 (4): 293–315. doi:. http://content2.apa.org/journals/rev/90/4/293.
- Tversky, A. and Kahneman, D. (1982) "Judgments of and by representativeness". In D. Kahneman, P. Slovic & A. Tversky (Eds.), Judgment under uncertainty: Heuristics and biases. Cambridge, UK: Cambridge University Press.