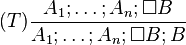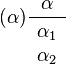Method of analytic tableaux
From Wikipedia, the free encyclopedia
In proof theory, the semantic tableau is a decision procedure for sentential and related logics, and a proof procedure for formulas of first-order logic. The tableau method can also determine the satisfiability of finite sets of formulas of various logics. It is the most popular proof procedure for modal logics (Girle 2000).
An analytic tableau has for each node a subformula of the formula at the origin. In other words, it is a tableau satisfying the subformula property.
Contents |
[edit] Introduction
For refutation tableaux, the objective is to show that the negation of a formula cannot be satisfied. There are rules for handling each of the usual connectives, starting with the main connective. In many cases, applying these rules causes the subtableau to divide into two. Quantifiers are instantiated. If any branch of a tableau leads to an evident contradiction, the branch closes. If all branches close, the proof is complete and the original formula is a logical truth.
Although the fundamental idea behind the analytic tableau method is derived from the cut-elimination theorem of structural proof theory, the origins of tableau calculi lie in the meaning (or semantics) of the logical connectives, as the connection with proof theory was made only in recent decades.
More specifically, a tableau calculus consists of a finite collection of rules with each rule specifying how to break down one logical connective into its constituent parts. The rules typically are expressed in terms of finite sets of formulae, although there are logics for which we must use more complicated data structures, such as multisets, lists, or even trees of formulas. Henceforth, "set" denotes any of {set, multiset, list, tree}.
If there is such a rule for every logical connective then the procedure will eventually produce a set which consists only of atomic formulae and their negations, which cannot be broken down any further. Such a set is easily recognizable as satisfiable or unsatisfiable with respect to the semantics of the logic in question. To keep track of this process, the nodes of a tableau itself are set out in the form of a tree and the branches of this tree are created and assessed in a systematic way. Such a systematic method for searching this tree gives rise to an algorithm for performing deduction and automated reasoning. Note that this larger tree is present regardless of whether the nodes contain sets, multisets, lists or trees.
[edit] Propositional logic
This section presents the tableau calculus for classical propositional logic. Tableau checks whether a given set of formulae is satisfiable or not. It can be used to check validity or entailment: a formula is valid if its negation is unsatisfiable and formulae  imply B if
imply B if  is unsatisfiable.
is unsatisfiable.
The main principle of propositional tableau is to attempt to "break" complex formulae into smaller ones until complementary pairs of literals are produced or no further expansion is possible.
The method works on a tree whose nodes are labeled with formulae. At each step, this tree is modified; in the propositional case, the only allowed changes are additions of nodes as descendant of a leaf. The procedure starts by generating the tree made of a chain of all formulae in the set to prove unsatisfiability. A variant to this starting step is to begin with a single-node tree whose root is labeled by  ; in this second case, the procedure can always copy a formula in the set below a leaf. As a running example, the tableau for the set
; in this second case, the procedure can always copy a formula in the set below a leaf. As a running example, the tableau for the set  is shown.
is shown.
The principle of tableau is that formulae in nodes of the same branch are considered in conjunction while the different branches are considered to be disjuncted. As a result, a tableau is a tree-like representation of a formula that is a disjunction of conjunctions. This formula is equivalent to the set to prove unsatisfiability. The procedure modifies the tableau in such a way that the formula represented by the resulting tableau is equivalent to the original one. One of these conjunctions may contain a pair of complementary literals, which proves that that conjunction is unsatisfiable. If all conjunctions are proved unsatisfiable, the original set of formulae is unsatisfiable.
[edit] And
Whenever a branch of a tableau contains a formula  that is the conjunction of two formulae, these two formulae are both consequences of that formula. This fact can be formalized by the following rule for expansion of a tableau:
that is the conjunction of two formulae, these two formulae are both consequences of that formula. This fact can be formalized by the following rule for expansion of a tableau:
(
) If a branch of the tableau contains a conjunctive formula
, add to its leaf the chain of two nodes containing the formulae A and B
This rule is generally written as follows:
A variant of this rule allows a node to contain a set of formulae rather than a single one. In this case, the formulae in this set are considered in conjunction, so one can add {A,B} at the end of a branch containing  . More precisely, if a node on a branch is labeled
. More precisely, if a node on a branch is labeled  , one can add to the branch the new leaf
, one can add to the branch the new leaf  .
.
[edit] Or
If a branch of a tableau contains a formula that is a disjunction of two formulae, such as  , the following rule can be applied:
, the following rule can be applied:
(
) If a node on a branch contains a disjunctive formula
, then create two sibling children to the leaf of the branch, containing the formulae A and B, respectively.
This rules splits a branch into two ones, differing only for the final node. Since branches are considered in disjunction to each other, the two resulting branches are equivalent to the original one, as the disjunction of their non-common nodes is precisely  . The rule for disjunction is generally formally written using the symbol | for separating the formulae of the two distinct nodes to be created:
. The rule for disjunction is generally formally written using the symbol | for separating the formulae of the two distinct nodes to be created:
If nodes are assumed to contain sets of formulae, this rule is replaced by: if a node is labeled  , a leaf of the branch this node is in can be appended two sibling child nodes labeled
, a leaf of the branch this node is in can be appended two sibling child nodes labeled 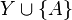 and
and  , respectively.
, respectively.
[edit] Not
The aim of tableau is to generate progressively simpler formulae until pairs of opposite literals are produced or no other rule can be applied. Negation can be treated by initially making formulae in negation normal form, so that negation only occurs in front of literals. Alternatively, one can use De Morgan's laws during the expansion of the tableau, so that for example  is treated as
is treated as  . Rules that introduce or remove a pair of negations (such as in
. Rules that introduce or remove a pair of negations (such as in  ) are also used in this case (otherwise, there would be no way of expanding a formula like
) are also used in this case (otherwise, there would be no way of expanding a formula like 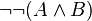 :
:
[edit] Closure
Every tableau can be considered as a graphical representation of a formula, which is equivalent to the set the tableau is built from. This formula is as follows: each branch of the tableau represents the conjunction of its formulae; the tableau represents the disjunction of its branches. The expansion rules transforms a tableau into one having an equivalent represented formula. Since the tableau is initialized as a single branch containing the formulae of the input set, all subsequent tableaux obtained from it represent formulae which are equivalent to that set (in the variant where the initial tableau is the single node labeled true, the formulae represented by tableaux are consequences of the original set.)
The method of tableaux works by starting with the initial set of formulae and then adding to the tableau simpler and simpler formulae, while still preserving equivalent to the original set, until contradiction is shown in the simple form of opposite literals. Since the formula represented by a tableau is the disjunction of the formulae represented by its branches, contradiction is obtained when every branch contains a pair of opposite literals.
Once a branch contains a literal and its negation, its corresponding formula is unsatisfiable. As a result, this branch can be now "closed", as there is no need to further expand it. If all branches of a tableau are closed, the formula represented by the tableau is unsatisfiable; therefore, the original set is unsatisfiable as well. Obtaining a tableau where all branches are closed is a way for proving the unsatisfiability of the original set. In the propositional case, one can also prove that satisfiability is proved by the impossibility of finding a closed tableau, provided that every expansion rule has been applied everywhere it could be applied. In particular, if a tableau contains some open (non-closed) branches and every formula that is not a literal has been used by a rule to generate a new node on every branch the formula is in, the set is satisfiable.
This rule takes into account that a formula may occur in more than one branch (this is the case if there is at least a branching point "below" the node). In this case, the rule for expanding the formula has to be applied so that its conclusion(s) are appended to all of these branches that are still open, before one can conclude that the tableau cannot be further expanded and that the formula is therefore satisfiable.
[edit] Set-labeled tableau
A variant of tableau is to label nodes with sets of formulae rather than single formulae. In this case, the initial tableau is a single node labeled with the set to be proved satisfiable. The formulae in a set are therefore considered to be in conjunction.
The rules of expansion of the tableau can now work on the leaves of the tableau, ignoring all internal nodes. For conjunction, the rule is based on the equivalence of a set containing a conjunction  with the set containing both A and B in place of it. In particular, if a leaf is labeled with
with the set containing both A and B in place of it. In particular, if a leaf is labeled with  , a node can be appended to it with label
, a node can be appended to it with label  :
:
For disjunction, a set  is equivalent to the disjunction of the two sets
is equivalent to the disjunction of the two sets  and
and  . As a result, if the first set labels a leaf, two children can be appended to it, labeled with the latter two formulae.
. As a result, if the first set labels a leaf, two children can be appended to it, labeled with the latter two formulae.
Finally, if a set contains both a literal and its negation, this branch can be closed:
A tableau for a given finite set X is a finite (upside down) tree with root X in which all child nodes are obtained by applying the tableau rules to their parents. A branch in such a tableau is closed if its leaf node contains "closed". A tableau is closed if all its branches are closed. A tableau is open if at least one branch is not closed.
Here are two closed tableaux for the set X = {r0 & ~r0, p0 & ((~p0 ∨ q0) & ~q0)} with each rule application marked at the right hand side (& and ~ stand for  and
and  , respectively)
, respectively)
{r0 & ~r0, p0 & ((~p0 v q0) & ~q0)} {r0 & ~r0, p0 & ((~p0 v q0) & ~q0)}
--------------------------------------(&) ------------------------------------------------------------(&)
{r0 , ~r0, p0 & ((~p0 v q0) & ~q0)} {r0 & ~r0, p0, ((~p0 v q0) & ~q0)}
-------------------------------------(id) ----------------------------------------------------------(&)
closed {r0 & ~r0, p0, (~p0 v q0), ~q0}
-------------------------------------------------------------(v)
{r0 & ~r0, p0, ~p0, ~q0} | {r0 & ~r0, p0, q0, ~q0}
-------------------------- (id) ---------------------- (id)
closed closed
The left hand tableau closes after only one rule application while the right hand one misses the mark and takes a lot longer to close. Clearly, we would prefer to always find the shortest closed tableaux but it can be shown that one single algorithm that finds the shortest closed tableaux for all input sets of formulae cannot exist.
The three rules  ,
,  and (id) given above are then enough to decide if a given set X' of formulae in negated normal form are jointly satisfiable:
and (id) given above are then enough to decide if a given set X' of formulae in negated normal form are jointly satisfiable:
Just apply all possible rules in all possible orders until we find a closed tableau for X' or until we exhaust all possibilities and conclude that every tableau for X' is open.
In the first case, X' is jointly unsatisfiable and in the second the case the leaf node of the open branch gives an assignment to the atomic formulae and negated atomic formulae which makes X' jointly satisfiable. Classical logic actually has the rather nice property that we need to investigate only (any) one tableau completely: if it closes then X' is unsatisfiable and if it is open then X' is satisfiable. But this property is not generally enjoyed by other logics.
These rules suffice for all of classical logic by taking an initial set of formulae X and replacing each member C by its logically equivalent negated normal form C' giving a set of formulae X' . We know that X is satisfiable if and only if X' is satisfiable, so it suffices to search for a closed tableau for X' using the procedure outlined above.
By setting  we can test whether the formula A is a tautology of classical logic:
we can test whether the formula A is a tautology of classical logic:
If the tableau for
closes then
is unsatisfiable and so A is a tautology since no assignment of truth values will ever make A false. Otherwise any open leaf of any open branch of any open tableau for
gives an assignment that falsifies A.
[edit] Conditional
Classical propositional logic usually has a connective to denote material implication. If we write this connective as ⇒, then the formula A ⇒ B stands for "if A then B". It is possible to give a tableau rule for breaking down A ⇒ B into its constituent formulae. Similarly, we can give one rule each for breaking down each of ¬(A ∧ B), ¬(A ∨ B), ¬(¬A), and ¬(A ⇒ B). Together these rules would give a terminating procedure for deciding whether a given set of formulae is simultaneously satisfiable in classical logic since each rule breaks down one formula into its constituents but no rule builds larger formulae out of smaller constituents. Thus we must eventually reach a node that contains only atoms and negations of atoms. If this last node matches (id) then we can close the branch, otherwise it remains open.
But note that the following equivalences hold in classical logic where (...) = (...) means that the left hand side formula is logically equivalent to the right hand side formula:

If we start with an arbitrary formula C of classical logic, and apply these equivalences repeatedly to replace the left hand sides with the right hand sides in C, then we will obtain a formula C' which is logically equivalent to C but which has the property that C' contains no implications, and ¬ appears in front of atomic formulae only. Such a formula is said to be in negation normal form and it is possible to prove formally that every formula C of classical logic has a logically equivalent formula C' in negation normal form. That is, C is satisfiable if and only if C' is satisfiable.
[edit] First-order logic tableau
Tableau are extended to first order by two rules for dealing with universal and existential quantifiers, respectively. Two different sets of rules can be used; both employ a form of Skolemization for handing existential quantifiers, but differ on the handling of universal quantifiers.
The set of formulae to check for validity is here supposed to contain no free variables; this is not a limitation as free variables are implicitly universally quantified, so universal quantifiers over these variables can be added, resulting in a formula with no free variables.
[edit] First-order tableau without unification
A first-order formula  implies all formulae γ(t) where t is a ground term. The following inference rule is therefore correct:
implies all formulae γ(t) where t is a ground term. The following inference rule is therefore correct:
 where t is an arbitrary ground term
where t is an arbitrary ground term
Contrarily to the rules for the propositional connectives, multiple applications of this rule to the same formula may be necessary. As an example, the set  can only be proved unsatisfiable if both P(a) and P(b) are generated from
can only be proved unsatisfiable if both P(a) and P(b) are generated from  .
.
Existential quantifiers are dealt with Skolemization. In particular, a formula with a leading existential quantifier like  generates its Skolemization δ(c), where c is a new constant symbol.
generates its Skolemization δ(c), where c is a new constant symbol.
 where c is a new constant symbol
where c is a new constant symbol
The Skolem term c is a constant (a function of arity 0) because the quantification over x does not occur within the scope of any universal quantifier. If the original formula contained some universal quantifiers such that the quantification over x was within their scope, these quantifiers have evidently been removed by the application of the rule for universal quantifiers.
The rule for existential quantifiers introduces new constant symbols. These symbols can be used by the rule for universal quantifiers, so that  can generate γ(c) even if c was not in the original formula but is a Skolem constant created by the rule for existential quantifiers.
can generate γ(c) even if c was not in the original formula but is a Skolem constant created by the rule for existential quantifiers.
The above two rules for universal and existential quantifiers are correct, and so are the propositional rules: if a set of formulae generates a closed tableau, this set is unsatisfiable. Completeness can also be proved: if a set of formulae is unsatisfiable, there exists a closed tableau built from it by these rules. However, actually finding such a closed tableau requires a suitable policy of application of rules. Otherwise, an unsatisfiable set can generate an infinite-growing tableau. As an example, the set  is unsatisfiable, but a closed tableau is never obtained if one unwisely keeps applying the rule for universal quantifiers to
is unsatisfiable, but a closed tableau is never obtained if one unwisely keeps applying the rule for universal quantifiers to  , generating for example
, generating for example  . A closed tableau can always be found by ruling out this and similar "unfair" policies of application of tableau rules.
. A closed tableau can always be found by ruling out this and similar "unfair" policies of application of tableau rules.
The rule for universal quantifiers 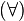 is the only non-deterministic rule, as it does not specify which term to instantiate with. Moreover, while the other rules need to be applied only once for each formula and each path the formula is in, this one may require multiple applications. Application of this rule can however be restricted by delaying the application of the rule until no other rule is applicable and by restricting the application of the rule to ground terms that already appear in the path of the tableau. The variant of tableaux with unification shown below aims at solving the problem of non-determinism.
is the only non-deterministic rule, as it does not specify which term to instantiate with. Moreover, while the other rules need to be applied only once for each formula and each path the formula is in, this one may require multiple applications. Application of this rule can however be restricted by delaying the application of the rule until no other rule is applicable and by restricting the application of the rule to ground terms that already appear in the path of the tableau. The variant of tableaux with unification shown below aims at solving the problem of non-determinism.
[edit] First-order tableau with unification
The main problem of tableau without unification is how to choose a ground term t for the universal quantifier rule. Indeed, every possible ground term can be used, but clearly most of them might be useless for closing the tableau.
A solution to this problem is to "delay" the choice of the term to the time when the consequent of the rule allows closing at least a branch of the tableau. This can be done by using a variable instead of a term, so that  generates γ(x'), and then allowing substitutions to later replace x' with a term. The rule for universal quantifiers becomes:
generates γ(x'), and then allowing substitutions to later replace x' with a term. The rule for universal quantifiers becomes:
 where x' is a variable not occurring everywhere else in the tableau
where x' is a variable not occurring everywhere else in the tableau
While the initial set of formulae is supposed not to contain free variables, a formula of the tableau contain the free variables generated by this rule. These free variables are implicitly considered universally quantified.
This rule employs a variable instead of a ground term. The gain of this change is that these variables can be then given a value when a branch of the tableau can be closed, solving the problem of generating terms that might be useless.
-
(σ) if σ is the most general unifier of two literals A and B, where A and the negation of B occur in the same branch of the tableau, σ can be applied at the same time to all formulae of the tableau
As an example,  can be proved unsatisfiable by first generating P(x1); the negation of this literal is unifiable with
can be proved unsatisfiable by first generating P(x1); the negation of this literal is unifiable with  , the most general unifier being the substitution that replaces x1 with a; applying this substitution results in replacing P(x1) with P(a), which closes the tableau.
, the most general unifier being the substitution that replaces x1 with a; applying this substitution results in replacing P(x1) with P(a), which closes the tableau.
This rule closes at least a branch of the tableau -the one containing the considered pair of literals. However, the substitution has to be applied to the whole tableau, not only on these two literals. This is expressed by saying that the free variables of the tableau are rigid: if an occurrence of a variable is replaced by something else, all other occurrences of the same variable must be replaced in the same way. Formally, the free variables are (implicitly) universally quantified and all formulae of the tableau are within the scope of these quantifiers.
Existential quantifiers are dealt with by Skolemization. Contrary to the tableau without unification, Skolem terms may not be simple constant. Indeed, formulae in a tableau with unification may contain free variables, which are implicitly considered universally quantified. As a result, a formula like  may be within the scope of universal quantifiers; if this is the case, the Skolem term is not a simple constant but a term made of a new function symbol and the free variables of the formula.
may be within the scope of universal quantifiers; if this is the case, the Skolem term is not a simple constant but a term made of a new function symbol and the free variables of the formula.
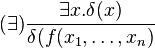 where f is a new function symbol and
where f is a new function symbol and 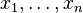 the free variables of δ
the free variables of δ
This rule incorporates a simplification over a rule where 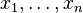 are the free variables of the branch, not of δ alone. This rule can be further simplified by the reuse of a function symbol if it has already been used in a formula that is identical to δ up to variable renaming.
are the free variables of the branch, not of δ alone. This rule can be further simplified by the reuse of a function symbol if it has already been used in a formula that is identical to δ up to variable renaming.
The formula represented by a tableau is obtained in a way that is similar to the propositional case, with the additional assumption that free variables are considered universally quantified. As for the propositional case, formulae in each branch are conjoined and the resulting formulae are disjoined. In addition, all free variables of the resulting formula are universally quantified. All these quantifiers have the whole formula in their scope. In other words, if F is the formula obtained by disjoining the conjunction of the formulae in each branch, and 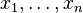 are the free variables in it, then
are the free variables in it, then 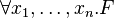 is the formula represented by the tableau. The following considerations apply:
is the formula represented by the tableau. The following considerations apply:
- The assumption that free variables are universally quantified is what makes the application of a most general unifier a sound rule: since γ(x') means that γ is true for every possible value of x', then γ(t) is true for the term t that the most general unifier replaces x with.
- Free variables in a tableau are rigid: all occurrences of the same variable have to be replaced all with the same term. Every variable can be considered a symbol representing a term that is yet to be decided. This is a consequence of free variables being assumed universally quantified over the whole formula represented by the tableau: if the same variable occurs free in two different nodes, both occurrences are in the scope of the same quantifier. As an example, if the formulae in two nodes are A(x) and B(x), where x is free in both, the formula represented by the tableau is something in the form
 . This formula implies that (...A(x)...B(x)...) is true for any value of x, but does not in general imply (...A(t)...A(t')...) for two different terms t and t', as these two terms may in general take different values. This means that x cannot be replaced by two different terms in A(x) and B(x).
. This formula implies that (...A(x)...B(x)...) is true for any value of x, but does not in general imply (...A(t)...A(t')...) for two different terms t and t', as these two terms may in general take different values. This means that x cannot be replaced by two different terms in A(x) and B(x).
- Free variables in a formula to check for validity are also considered universally quantified. However, these variables cannot be left free when building a tableau, because tableau rules works on the converse of the formula but still treats free variables as universally quantified. For example,
 is not valid (it is not true in the model where
is not valid (it is not true in the model where  , and the interpretation where x = 2). Consequently,
, and the interpretation where x = 2). Consequently,  is satisfiable (it is satisfied by the same model and interpretation). However, a closed tableau could be generated with P(x) and
is satisfiable (it is satisfied by the same model and interpretation). However, a closed tableau could be generated with P(x) and 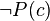 , and substituting x with c would generate a closure. A correct procedure is to first make universal quantifiers explicit, thus generating
, and substituting x with c would generate a closure. A correct procedure is to first make universal quantifiers explicit, thus generating  .
.
The following two variants are also correct.
- Applying to the whole tableau a substitution to the free variables of the tableau is a correct rule, provided that this substitution is free for the formula representing the tableau. In other worlds, applying such a substitution leads to a tableau whose formula is still a consequence of the input set. Using most general unifiers automatically ensures that the condition of freeness for the tableau is met.
- While in general every variable has to be replaced with the same term in the whole tableau, there are some special cases in which this is not necessary.
Tableau with unification can be proved complete: if a set of formulae is unsatisfiable, it has a tableau-with-unification proof. However, actually finding such a proof may be a difficult problem. Contrarily to the case without unification, applying a substitution can modify the existing part of a tableau; while applying a substitution closes at least a branch, it may make other branches impossible to close (even if the set is unsatisfiable).
A solution to this problem is that delayed instantiation: no substitution is applied until one that closes all branches at the same time is found. With this variant, a proof for an unsatisfiable set can always be found by a suitable policy of application of the other rules. This method however requires the whole tableau to be kept in memory: the general method closes branches which can be then discarded, while this variant does not close any branch until the end.
The problem that some tableau that can be generated are impossible to close even if the set is unsatisfiable is common to other sets of tableau expansion rules: even if some specific sequences of application of these rules allow constructing a closed tableau (if the set is unsatisfiable), some other sequences lead to tableau that cannot be closed. General solutions for these cases are outlined in the "Searching for a tableau" section.
[edit] Tableau calculi and their properties
A tableau calculus is a set of rules that allows building and modification of a tableau. Propositional tableau rules, tableau rules without unification, and tableau rules with unification, are all tableau calculi. Some important properties a tableau calculus may or may not possess are completeness, destructiveness, and proof confluence.
A tableau calculi is said complete if it allows building a tableau proof for every given unsatisfiable set of formulae. The tableau calculi mentioned above can be proved complete.
A remarkable difference between tableau with unification and the other two calculi is that the latter two calculi only modify a tableau by adding new nodes to it, while the former one allows substitutions to modify the existing part of the tableau. More generally, tableau calculi are classed as destructive or non-destructive depending on whether they only add new nodes to tableau or not. Tableau with unification is therefore destructive, while propositional tableau and tableau without unification are non-destructive.
Proof confluence is the property of a tableau calculus to obtain a proof for an arbitrary unsatisfiable set from an arbitrary tableau, assuming that this tableau has itself been obtained by applying the rules of the calculus. In other words, in a proof confluent tableau calculus, from an unsatisfiable set one can apply whatever set of rules and still obtain a tableau from which a closed one can be obtained by applying some other rules.
[edit] Proof procedures
A tableau calculus is simply a set of rules that tells how a tableau can be modified. A proof procedure is a method for actually finding a proof (if one exists). In other words, a tableau calculus is a set of rules, while a proof procedure is a policy of application of these rules. Even if a calculus is complete, not every possible choice of application of rules leads to a proof of an unsatisfiable set. For example 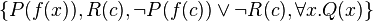 is unsatisfiable, but both tableaux with unification and tableaux without unification allow the rule for the universal quantifiers to be applied repeatedly to the last formula, while simply applying the rule for disjunction to the third one would directly lead to closure.
is unsatisfiable, but both tableaux with unification and tableaux without unification allow the rule for the universal quantifiers to be applied repeatedly to the last formula, while simply applying the rule for disjunction to the third one would directly lead to closure.
For proof procedures, a definition of completeness has been given: a proof procedure is strongly complete if it allows finding a closed tableau for any given unsatisfiable set of formulae. Proof confluence of the underlying calculus is relevant to completeness: proof confluence is the guarantee that a closed tableau can be always generated from an arbitrary partially constructed tableau (if the set is unsatisfiable). Without proof confluence, the application of a 'wrong' rule may result in the impossibility of making the tableau complete by applying other rules.
Propositional tableaux and tableaux without unification have strongly complete proof procedures. In particular, a complete proof procedure is that of applying the rules in a fair way. This is because the only way such calculi cannot generate a closed tableau from an unsatisfiable set is by not applying some applicable rules.
For propositional tableaux, fairness amounts to expanding every formula in every branch. More precisely, for every formula and every branch the formula is in, the rule having the formula as a precondition has been used to expand the branch. A fair proof procedure for propositional tableaux is strongly complete.
For first-order tableaux without unification, the condition of fairness is similar, with the exception that the rule for universal quantifier might require more than one application. Fairness amounts to expanding every universal quantifier infinitely often. In other words, a fair policy of application of rules cannot keep applying other rules without expanding every universal quantifier in every branch that is still open once in a while.
[edit] Searching for a closed tableau
If a tableau calculus is complete, every unsatisfiable set of formula has an associated closed tableau. While this tableau can always be obtained by applying some of the rules of the calculus, the problem of which rules to apply for a given formula still remains. As a result, completeness does not automatically implies the existence of a feasible policy of application of rules that can always lead to building a closed tableau for every given unsatisfiable set of formulae. While a fair proof procedure is complete for ground tableau and tableau without unification, this is not the case for tableau with unification.
A general solution for this problem is that of searching the space of tableau until a closed one is found (if any exists, that is, the set is unsatisfiable). In this approach, one starts with an empty tableau and then recursively tries to apply every possible applicable rule. This procedure visit a (implicit) tree whose nodes are labeled with tableau, and such that the tableau in a node is obtained from the tableau in its parent by applying one of the valid rules.
Since one such branch can be infinite, this tree has to be visited breadth-first rather than depth-first. This requires a large amount of space, as the breadth of the tree can grow exponentially. A method that may visit some nodes more than once but works in polynomial space is to visit in a depth-first manner with iterative deepening: one first visits the tree up to a certain depth, then increases the depth and perform the visit again. This particular procedure uses the depth (which is also the number of tableau rules that have been applied) for deciding when to stop at each step. Various other parameters (such as the size of the tableau labeling a node) have been used instead.
[edit] Reducing search
The size of the search tree depends on the number of (children) tableau that can be generated from a given (parent) one. Reducing the number of such tableau therefore reduces the required search.
A way for reducing this number is to disallow the generation of some tableau based on their internal structure. An example is the condition of regularity: if a branch contains a literal, using an expansion rule that generates the same literal is useless because the branch containing two copies of the literals would have the same set of formulae of the original one. This expansion can be disallowed because if a closed tableau exists, it can be found without it. This restriction is structural because it can be checked by looking at the structure of the tableau to expand only.
Different methods for reducing search disallow the generation of some tableau on the ground that a closed tableau can still be found by expanding the other ones. These restrictions are called global. As an example of a global restriction, one may employ a rule that specify which of the open branches is to be expanded. As a result, if a tableau has for example two non-closed branches, the rule tells which one is to be expanded, disallowing the expansion of the second one. This restriction reduces the search space because one possible choice is now forbidden; completeness if however not harmed, as the second branch will still be expanded if the first one is eventually closed. As an example, a tableau with root  , child
, child 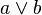 , and two leaves a and b can be closed in two ways: applying
, and two leaves a and b can be closed in two ways: applying  first to a and then to b, or vice versa. There is clearly no need to follow both possibilities; one may consider only the case in which
first to a and then to b, or vice versa. There is clearly no need to follow both possibilities; one may consider only the case in which  is first applied to a and disregard the case in which it is first applied to b. This is a global restriction because what allows neglecting this second expansion is the presence of the other tableau, where expansion is applied to a first and b afterwards.
is first applied to a and disregard the case in which it is first applied to b. This is a global restriction because what allows neglecting this second expansion is the presence of the other tableau, where expansion is applied to a first and b afterwards.
[edit] Clause tableaux
When applied to sets of clauses (rather than of arbitrary formulae), tableaux methods allow for a number of efficiency improvements. A first-order clause is a formula  that does not contain free variables and such that each Li is a literal. The universal quantifiers are often omitted for clarity, so that for example
that does not contain free variables and such that each Li is a literal. The universal quantifiers are often omitted for clarity, so that for example  actually means
actually means  . Note that, if taken literally, these two formulae are not the same as for satisfiability: rather, the satisfiability
. Note that, if taken literally, these two formulae are not the same as for satisfiability: rather, the satisfiability  is the same as that of
is the same as that of  . That free variables are universally quantified is not a consequence of the definition of first-order satisfiability; it is rather used as an implicit common assumption when dealing with clauses.
. That free variables are universally quantified is not a consequence of the definition of first-order satisfiability; it is rather used as an implicit common assumption when dealing with clauses.
The only expansion rules that are applicable to a clause are 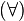 and
and  ; these two rules can be replaced by their combination without losing completeness. In particular, the following rule corresponds to applying in sequence the rules
; these two rules can be replaced by their combination without losing completeness. In particular, the following rule corresponds to applying in sequence the rules 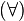 and
and  of the first-order calculus with unification.
of the first-order calculus with unification.
 where
where  is obtained by replacing every variable with a new one in
is obtained by replacing every variable with a new one in 
When the set to be checked for satisfiability is only composed of clauses, this and the unification rules are sufficient to prove unsatisfiability. In other worlds, the tableau calculi composed of (C) and (σ) is complete.
Since the clause expansion rule only generates literals and never new clauses, the clauses to which it can be applied are only clauses of the input set. As a result, the clause expansion rule can be further restricted to the case where the clause is in the input set.
 where
where  is obtained by replacing every variable with a
is obtained by replacing every variable with a
new one in  , which is a clause of the input set
, which is a clause of the input set
Since this rule directly exploit the clauses in the input set there is no need to initialize the tableau to the chain of the input clauses. The initial tableau can therefore be initialize with the single node labeled true; this label is often omitted as implicit. As a result of this further simplification, every node of the tableau (apart of the root) is labeled with a literal.
A number of optimizations can be used for clause tableau. These optimization are aimed at reducing the number of possible tableaux to be explored when searching for a closed tableau as described in the "Searching for a closed tableau" section above.
[edit] Connection tableau
Connection is a condition over tableau that forbids expanding a branch using clauses that are unrelated to the literals that are already in the branch. Connection and be defined in two ways:
- strong connectedness
- when expanding a branch, use an input clause only if it contains a literal that can be unified with the negation of the literal in the current leaf
- weak connectedness
- allow the use of clauses that contain a literal that unifies with the negation of a literal on the branch
Both conditions apply only to branches not only comprised of the root. The second definition allows for the use of a clause containing a literal that unifies with the negation of a literal in the branch, while the first only further constraint that literal to be in leaf of the current branch.
If clause expansion is restricted by connectedness (either strong or weak), its application produces a tableau in which substitution can applied to one of the new leaves, closing its branch. In particular, this is the leaf containing the literal of the clause that unifies with the negation of a literal in the branch (or the negation of the literal in the parent, in case of strong connection).
Both conditions of connectedness lead to a complete first-order calculus: if a set of clauses is unsatisfiable, it has a closed connected (strongly or weakly) tableau. Such a closed tableau can be found by searching in the space of tableaux as explained in the "Searching for a closed tableau" section. During this search, connectedness eliminates some possible choices of expansion, thus reducing search. In other worlds, while the tableau in a node of the tree can be in general expanded in several different ways, connection may allow only few of them, thus reducing the number of resulting tableaux that need to be further expanded.
This can be seen on the following (propositional) example. The tableau made of a chain true − a for the set of clauses 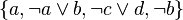 can be in general expanded using each of the four input clauses, but connection only allows the expansion that uses
can be in general expanded using each of the four input clauses, but connection only allows the expansion that uses 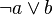 . This means that the tree of tableaux has four leaves in general but only one if connectedness is imposed. This means that connectedness leaves only one tableau to try and expand, instead of the four ones to consider in general. In spite of this reduction of choices, the completeness theorem implies that a closed tableau can be found if the set is unsatisfiable.
. This means that the tree of tableaux has four leaves in general but only one if connectedness is imposed. This means that connectedness leaves only one tableau to try and expand, instead of the four ones to consider in general. In spite of this reduction of choices, the completeness theorem implies that a closed tableau can be found if the set is unsatisfiable.
The connectedness conditions, when applied to the propositional (clausal) case, make the resulting calculus non-confluent. As an example,  is unsatisfiable, but applying (C) to a generates the chain true − a, which is not closed and to which no other expansion rule can be applied without violating either strong or weak connectedness. In the case of weak connectedness, confluence holds provided that the clause used for expanding the root is relevant to unsatisfiability, that is, it is contained in a minimally unsatisfiable subset of the set of clauses. Unfortunately, the problem of checking whether a clause meets this condition is itself a hard problem. In spite of non-confluence, a closed tableau can be found using search, as presented in the "Searching for a closed tableau" section above. While search is made necessary, connectedness reduces the possible choices of expansion, thus making search more efficient.
is unsatisfiable, but applying (C) to a generates the chain true − a, which is not closed and to which no other expansion rule can be applied without violating either strong or weak connectedness. In the case of weak connectedness, confluence holds provided that the clause used for expanding the root is relevant to unsatisfiability, that is, it is contained in a minimally unsatisfiable subset of the set of clauses. Unfortunately, the problem of checking whether a clause meets this condition is itself a hard problem. In spite of non-confluence, a closed tableau can be found using search, as presented in the "Searching for a closed tableau" section above. While search is made necessary, connectedness reduces the possible choices of expansion, thus making search more efficient.
[edit] Regular tableaux
A tableau is regular if no literal occurs twice in the same branch. Enforcing this condition allows for a reduction of the possible choices of tableau expansion, as the clauses that would generate a non-regular tableau cannot be expanded.
These disallowed expansion steps are however useless. If B is a branch containing a literal L, and C is a clause whose expansion violates regularity, then C contains L. In order to close the tableau, one needs to expand and close, among others, the branch where B − L, where L occurs twice. However, the formulae in this branch are exactly the same as the formulae of B alone. As a result, the same expansion steps that close B − L also close B. This means that expanding C was unnecessary; moreover, if C contained other literals, its expansion generated other leaves that needed to be closed. In the propositional case, the expansion needed to close these leaves are completely useless; in the first-order case, they may only affect the rest of the tableau because of some unifications; these can however be combined to the substitutions used to close the rest of the tableau.
[edit] Tableaux for modal logics
In a modal logic, a model comprises a set of possible worlds, each one associated to a truth evaluation; an accessibility relation tells when a world is accessible from another one. A modal formula may specify not only conditions over a possible world, but also on the ones that are accessible from it. As an example,  is true in a world if A is true in all worlds that are accessible from it.
is true in a world if A is true in all worlds that are accessible from it.
As for propositional logic, tableaux for modal logics are based on recursively breaking formulae into its basic components. Expanding a modal formula may however require stating conditions over different worlds. As an example, if  is true in a world then there exists a world accessible from it where A is false. However, one cannot simply add the following rule to the propositional ones.
is true in a world then there exists a world accessible from it where A is false. However, one cannot simply add the following rule to the propositional ones.
In propositional tableaux all formulae refer to the same truth evaluation, but the precondition of the rule above holds in a world while the consequence holds in another. Not taking into account this would generate wrong results. For example, formula  states that a is true in the current world and a is false in a world that is accessible from it. Simply applying
states that a is true in the current world and a is false in a world that is accessible from it. Simply applying  and the expansion rule above would produce a and
and the expansion rule above would produce a and  , but these two formulae should not in general generate a contradiction, as they hold in different worlds. Modal tableaux calculi do contain rules of the kind of the one above, but include mechanisms to avoid the incorrect interaction of formulae referring to different worlds.
, but these two formulae should not in general generate a contradiction, as they hold in different worlds. Modal tableaux calculi do contain rules of the kind of the one above, but include mechanisms to avoid the incorrect interaction of formulae referring to different worlds.
Technically, tableaux for modal logics check the satisfiability of a set of formulae: they check whether there exists a model M and world w such that the formulae in the set are true in that model and world. In the example above, while a states the truth of a in w, the formula  states the truth of
states the truth of  in some world w' that is accessible from w and which may in general be different from w. Tableaux calculi for modal logic take into account that formulae may refer to different worlds.
in some world w' that is accessible from w and which may in general be different from w. Tableaux calculi for modal logic take into account that formulae may refer to different worlds.
This fact has an important consequence: formulae that hold in a world may imply conditions over different successors of that world. Unsatisfiability may then be proved from the subset of formulae referring to the a single successor. This holds if a world may have more than one successor, which is true for most modal logic. If this is the case, a formula like 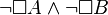 is true if a successor where
is true if a successor where  holds exists and a successor where
holds exists and a successor where  holds exists. In the other way around, if one can show unsatisfiability of
holds exists. In the other way around, if one can show unsatisfiability of  in an arbitrary successor, the formula is proved unsatisfiable without checking for worlds where
in an arbitrary successor, the formula is proved unsatisfiable without checking for worlds where  holds. At the same time, if one can show unsatisfiability of
holds. At the same time, if one can show unsatisfiability of  , there is no need to check
, there is no need to check  . As a result, while there are two possible way to expand
. As a result, while there are two possible way to expand 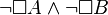 , one of these two ways is always sufficient to prove unsatisfiability if the formula is unsatisfiable. For example, one may expand the tableau by considering an arbitrary world where
, one of these two ways is always sufficient to prove unsatisfiability if the formula is unsatisfiable. For example, one may expand the tableau by considering an arbitrary world where  holds. If this expansion leads to unsatisfiability, the original formula is unsatisfiable. However, it is also possible that unsatisfiability cannot be proved this way, and that the world where
holds. If this expansion leads to unsatisfiability, the original formula is unsatisfiable. However, it is also possible that unsatisfiability cannot be proved this way, and that the world where  holds should have been considered instead. As a result, one can always prove unsatisfiability by expanding either
holds should have been considered instead. As a result, one can always prove unsatisfiability by expanding either  only or
only or  only; however, if the wrong choice is done the resulting tableau may not be closed. Expanding either subformula leads to tableau calculi that are complete but not proof-confluent. Searching as described in the "Searching for a closed tableau" may therefore be necessary.
only; however, if the wrong choice is done the resulting tableau may not be closed. Expanding either subformula leads to tableau calculi that are complete but not proof-confluent. Searching as described in the "Searching for a closed tableau" may therefore be necessary.
Depending on whether the precondition and consequence of a tableau expansion rule refer to the same world or not, the rule is called static or transactional. While rules for propositional connectives are all static, not all rules for modal connectives are transactional: for example, in every modal logic including axiom T, it holds that  implies A in the same world. As a result, the relative (modal) tableau expansion rule is static, as both its precondition and consequence refer to the same world.
implies A in the same world. As a result, the relative (modal) tableau expansion rule is static, as both its precondition and consequence refer to the same world.
[edit] Formula-deleting tableau
A way for making formulae referring to different worlds not interacting in the wrong way is to make sure that all formulae of a branch refer to the same world. This condition is initially true as all formulae in the set to be checked for consistency are assumed referring to the same world. When expanding a branch, two situations are possible: either the new formulae refer to the same world as the other one in the branch or not. In the first case, the rule is applied normally. In the second case, all formulae of the branch that do not also hold in the new world are deleted from the branch, and possibly added to all other branches that are still relative to the old world.
As an example, in S5 every formula  that is true in a world is also true in all accessible worlds (that is, in all accessible worlds both A and
that is true in a world is also true in all accessible worlds (that is, in all accessible worlds both A and  are true). Therefore, when applying
are true). Therefore, when applying  , whose consequence holds in a different world, one deletes all formulae from the branch, but can keep all formulae
, whose consequence holds in a different world, one deletes all formulae from the branch, but can keep all formulae  , as these hold in the new world as well. In order to retain completeness, the deleted formulae are then added to all other branches that still refer to the old world.
, as these hold in the new world as well. In order to retain completeness, the deleted formulae are then added to all other branches that still refer to the old world.
[edit] World-labeled tableau
A different mechanism for ensuring the correct interaction between formulae referring to different worlds is to switch from formulae to labeled formulae: instead of writing A, one would write w:A to make it explicit that A holds in world w.
All propositional expansion rules are adapted to this variant by stating that they all refer to formulae with the same world label. For example,  generates two nodes labeled with w:A and w:B; a branch is closed only if it contains two opposite literals of the same world, like w:a and
generates two nodes labeled with w:A and w:B; a branch is closed only if it contains two opposite literals of the same world, like w:a and  ; no closure is generated if the two world labels are different, like in w:a and
; no closure is generated if the two world labels are different, like in w:a and  .
.
The modal expansion rule may have a consequence that refer to a different worlds. For example, the rule for  would be written as follows
would be written as follows
The precondition and consequent of this rule refer to worlds w and w', respectively. The various different calculi use different methods for keeping track of the accessibility of the worlds used as labels. Some include pseudo-formulae like wRw' to denote that w' is accessible from w. Some others use sequences of integers as world labels, this notation implicitly representing the accessibility relation (for example, (1,4,2,3) is accessible from (1,4,2).)
[edit] Set-labeling tableaux
The problem of interaction between formulae holding in different worlds can be overcome by using set-labeling tableaux. These are trees whose nodes are labeled with sets of formulae; the expansion rules tell how to attach new nodes to a leaf, based only on the label of the leaf (and not on the label of other nodes in the branch).
Tableaux for modal logics are used to verify the satisfiability of a set of modal formulae in a given modal logic. Given a set of formulae S, they check the existence of a model M and a world w such that  .
.
The expansion rules depend on the particular modal logic used. A tableau system for the basic modal logic K can be obtained by adding to the propositional tableau rules the following one:
Intuitively, the precondition of this rule expresses the truth of all formulae  at all accessible worlds, and truth of
at all accessible worlds, and truth of  at some accessible worlds. The consequence of this rule is a formula that must be true at one of those worlds where
at some accessible worlds. The consequence of this rule is a formula that must be true at one of those worlds where  is true.
is true.
More technically, modal tableaux methods check the existence of a model M and a world w that make set of formulae true. If  are true in w, there must be a world w' that is accessible from w and that makes
are true in w, there must be a world w' that is accessible from w and that makes  true. This rule therefore amounts to deriving a set of formulae that must be satisfied in such w'.
true. This rule therefore amounts to deriving a set of formulae that must be satisfied in such w'.
While the preconditions  are assumed satisfied by M,w, the consequences
are assumed satisfied by M,w, the consequences  are assumed satisfied in M,w': same model but possibly different worlds. Set-labeled tableaux do not explicitly keep track of the world where each formula is assumed true: two nodes may or may not refer to the same world. However, the formulae labeling any given node are assumed true at the same world.
are assumed satisfied in M,w': same model but possibly different worlds. Set-labeled tableaux do not explicitly keep track of the world where each formula is assumed true: two nodes may or may not refer to the same world. However, the formulae labeling any given node are assumed true at the same world.
As a result of the possibly different worlds where formulae are assumed true, a formula in a node is not automatically valid in all its descendants, as every application of the modal rule correspond to a move from a world to another one. This condition is automatically captured by set-labeling tableaux, as expansion rules are based only on the leaf where they are applied and not on its ancestors.
Remarkably, (K) does not directly extend to multiple negated boxed formulae such as in  : while there exists an accessible world where B1 is false and one in which B2 is false, these two worlds are not necessarily the same.
: while there exists an accessible world where B1 is false and one in which B2 is false, these two worlds are not necessarily the same.
Differently from the propositional rules, (K) states conditions over all its preconditions. For example, it cannot be applied to a node labeled by 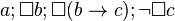 ; while this set is inconsistent and this could be easily proved by applying (K), this rule cannot be applied because of formula a, which is not even relevant to inconsistency. Removal of such formulae is made possible by the rule:
; while this set is inconsistent and this could be easily proved by applying (K), this rule cannot be applied because of formula a, which is not even relevant to inconsistency. Removal of such formulae is made possible by the rule:
The addition of this rule (thinning rule) makes the resulting calculus non-confluent: a tableau for an inconsistent set may be impossible to close, even if a closed tableau for the same set exists.
Rule (θ) is non-deterministic: the set of formulae to be removed (or to be kept) can be chosen arbitrarily; this creates the problem of choosing a set of formulae to discard that is not so large it makes the resulting set satisfiable and not so small it makes the necessary expansion rules inapplicable. Having a large number of possible choices makes the problem of searching for a closed tableau harder.
This non-determinism can be avoided by restricting the usage of (θ) so that it is only applied before a modal expansion rule, and so that it only removes the formulae that make that other rule inapplicable. This condition can be also formulated by merging the two rules in a single one. The resulting rule produces the same result as the old one, but implicitly discard all formulae that made the old rule inapplicable. This mechanism for removing (θ) has been proved to preserve completeness for many modal logics.
Axiom T expresses reflexivity of the accessibility relation: every world is accessible from itself. The corresponding tableau expansion rule is:
This rule relates conditions over the same world: if 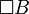 is true in a world, by reflexivity B is also true in the same world. This rule is static, not transactional, as both its precondition and consequent refer to the same world.
is true in a world, by reflexivity B is also true in the same world. This rule is static, not transactional, as both its precondition and consequent refer to the same world.
This rule copies 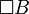 from the precondition to the consequent, in spite of this formula having being "used" to generate B. This is correct, as the considered world is the same, so
from the precondition to the consequent, in spite of this formula having being "used" to generate B. This is correct, as the considered world is the same, so 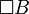 also holds there. This "copying" is necessary in some cases. It is for example necessary to prove the inconsistency of
also holds there. This "copying" is necessary in some cases. It is for example necessary to prove the inconsistency of  : the only applicable rules are in order
: the only applicable rules are in order 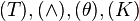 , from which one is blocked if
, from which one is blocked if  is not copied.
is not copied.
[edit] Auxiliary tableaux
A different method for dealing with formulae holding in alternate worlds is to start a different tableau for each now world that is introduced in the tableau. For example,  implies that A is false in an accessible world, so one starts a new tableau rooted by
implies that A is false in an accessible world, so one starts a new tableau rooted by  . This new tableau is attached to the node of the original tableau where the expansion rule has been applied; a closure of this tableau immediately generates a closure of all branches where that node is, regardless of whether the same node is associated other auxiliary tableaux. The expansion rules for the auxiliary tableaux are the same as for the original one; therefore, an auxiliary tableau can have in turns other (sub-)auxiliary tableaux.
. This new tableau is attached to the node of the original tableau where the expansion rule has been applied; a closure of this tableau immediately generates a closure of all branches where that node is, regardless of whether the same node is associated other auxiliary tableaux. The expansion rules for the auxiliary tableaux are the same as for the original one; therefore, an auxiliary tableau can have in turns other (sub-)auxiliary tableaux.
[edit] Global assumptions
The above modal tableaux establish the consistency of a set of formulae, and can be used for solving the local logical consequence problem. This is the problem of telling whether, for each model M, if A is true in a world w, then B is also true in the same world. This is the same as checking whether B is true in a world of a model, in the assumption that A is also true in the same world of the same model.
A related problem is the global consequence problem, where the assumption is that a formula (or set of formulae) G is true in all possible worlds of the model. The problem is that of checking whether, in all models M where G is true in all worlds, B is also true in all worlds.
Local and global assumption differ on models where the assumed formula is true in some worlds but not in others. As an example,  entails
entails  globally but not locally. Local entailment does not hold in a model comprised of two worlds making P and
globally but not locally. Local entailment does not hold in a model comprised of two worlds making P and  true, respectively, and where the second is accessible from the first; in the first world, the assumption is true but
true, respectively, and where the second is accessible from the first; in the first world, the assumption is true but  is false. This counterexample works because P can be assumed true in a world and false in another one. If however the same assumption is considered global,
is false. This counterexample works because P can be assumed true in a world and false in another one. If however the same assumption is considered global,  is not allowed in any world of the model.
is not allowed in any world of the model.
These two problems can be combined, so that one can check whether B is a local consequence of A under the global assumption G. Tableaux calculi can deal with global assumption by a rule allowing its addition to every node, regardless of the world it refers to.
[edit] Notations
The following conventions are sometimes used.
[edit] Uniform notation
When writing tableaux expansion rules, formulae are often denoted using a convention, so that for example α is always considered to be 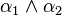 . The following table provides the notation for formulae in propositional, first-order, and modal logic.
. The following table provides the notation for formulae in propositional, first-order, and modal logic.
| Notation | Formulae | ||
|---|---|---|---|
| α | 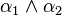 |
 |
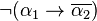 |
| β |  |
 |
 |
| γ |  |
 |
|
| δ |  |
 |
|
| π |  |
 |
|
| υ |  |
 |
|
Each label in the first column is taken to be either formula in the other columns. An overlined formula such as 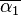 indicates that α1 is the negation of whatever formula appears in its place, so that for example in formula
indicates that α1 is the negation of whatever formula appears in its place, so that for example in formula  the subformula α1 is the negation of a.
the subformula α1 is the negation of a.
Since every label indicates many equivalent formulae, this notation allows writing a single rule for all these equivalent formulae. For example, the conjunction expansion rule is formulated as:
[edit] Signed formulae
A formula in a tableau is assumed true. Signed tableaux allows stating that a formula is false. This is generally achieved by adding a label to each formula, where the label T indicates formulae assumed true and F those assumed false. A different but equivalent notation is that to write formulae that are assumed true at the left of the node and formulae assumed false at its right.
[edit] References
- Bostock, David, 1997. Intermediate Logic. Oxford Univ. Press.
- M D'Agostino, D Gabbay, R Haehnle, J Posegga (Eds), Handbook of Tableau Methods, Kluwer,1999.
- Girle, Rod, 2000. Modal Logics and Philosophy. Teddington UK: Acumen.
- Goré, Rajeev (1999) "Tableau Methods for Modal and Temporal Logics" in D'Agostino, M., Dov Gabbay, R. Haehnle, and J. Posegga, eds., Handbook of Tableau Methods. Kluwer: 297-396.
- Richard Jeffrey, 1990 (1967). Formal Logic: Its Scope and Limits, 3rd ed. McGraw Hill.
- Raymond Smullyan, 1995 (1968). First Order-Logic. Dover Publications.
- Melvin Fitting (1996). First-order logic and automated theorem proving (2nd ed.). Springer-Verlag.
- Reiner Hähnle (2001). Tableaux and Related Methods. Handbook of Automated Reasoning
- Reinhold Letz, Gernot Stenz (2001). Model Elimination and Connection Tableau Procedures. Handbook of Automated Reasoning
- Zeman, J. J. (1973) Modal Logic. Reidel.



 generates
generates 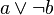 and
and 







 : all rules have been applied to every formula on every branch, but the tableau is not closed (only the left branch is closed), as expected for satisfiable sets
: all rules have been applied to every formula on every branch, but the tableau is not closed (only the left branch is closed), as expected for satisfiable sets
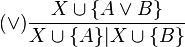


 . For clarity, formulae are numbered on the left and the formula and rule used at each step is on the right
. For clarity, formulae are numbered on the left and the formula and rule used at each step is on the right

 . For simplicity, the formulae of the set have been omitted from all tableau in the figure and a rectangle used in their place. A closed tableau is in the bold box; the other branches could be still expanded.
. For simplicity, the formulae of the set have been omitted from all tableau in the figure and a rectangle used in their place. A closed tableau is in the bold box; the other branches could be still expanded.