Abductive reasoning
From Wikipedia, the free encyclopedia
Abduction, or inference to the best explanation, is a method of reasoning in which one chooses the hypothesis that would, if true, best explain the relevant evidence. Abductive reasoning starts from a set of accepted facts and infers their most likely, or best, explanations. The term abduction is also sometimes used to just mean the generation of hypotheses to explain observations or conclusions, but the former definition is more common both in philosophy and computing.
Contents |
[edit] Deduction, induction, and abduction
- Deduction
- allows deriving b as a consequence of a. In other words, deduction is the process of deriving the consequences of what is assumed. Given the truth of the assumptions, a valid deduction guarantees the truth of the conclusion. It is true by definition and is independent of sense experience. For example, if it is true (given) that the sum of the angles is 180° in all triangles, and if a certain triangle has angles of 90° and 30°, then it can be deduced that the third angle is 60°.
- Induction
- allows inferring a from multiple instantiations of b when a entails b. Induction is the process of inferring probable antecedents as a result of observing multiple consequents. An inductive statement requires empirical evidence for it to be true. For example, the statement 'it is snowing outside' is invalid until one looks or goes outside to see whether it is true or not. Induction requires sense experience.
- Abduction
- allows inferring a as an explanation of b. Because of this, abduction allows the precondition a to be inferred from the consequence b. Deduction and abduction thus differ in the direction in which a rule like “a entails b” is used for inference. As such abduction is formally equivalent to the logical fallacy affirming the consequent or Post hoc ergo propter hoc, because there are multiple possible explanations for b.
Unlike deduction and in some sense induction, abduction can produce results that are incorrect within its formal system. Hence the conclusions of abduction can only be made valid by separately checking them with a different method, either by deduction or exhaustive induction. However, it can still be useful as a heuristic, especially when something is known about the likelihood of different causes for b.
[edit] Logic-based abduction
In logic, explanation is done from a logical theory T representing a domain and a set of observations O. Abduction is the process of deriving a set of explanations of O according to T and picking out one of those explanations. For E to be an explanation of O according to T, it should satisfy two conditions:
- O follows from E and T;
- E is consistent with T.
In formal logic, O and E are assumed to be sets of literals. The two conditions for E being an explanation of O according to theory T are formalized as:
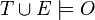 ;
; is consistent.
is consistent.
Among the possible explanations E satisfying these two conditions, some other condition of minimality is usually imposed to avoid irrelevant facts (not contributing to the entailment of O) being included in the explanations. Abduction is then the process that picks out some member of E. Criteria for picking out a member representing "the best" explanation include the simplicity, the prior probability, or the explanatory power of the explanation.
A proof theoretical abduction method for first order classical logic based on the sequent calculus and a dual one, based on semantic tableaux (analytic tableaux) have been proposed[citation needed]. The methods are sound and complete and work for full first order logic, without requiring any preliminary reduction of formulae into normal forms. These methods have also been extended to modal logic.
Abductive logic programming is a computational framework that extends normal logic programming with abduction. It separates the theory T into two components, one of which is a normal logic program, used to generate E by means of backward reasoning, the other of which is a set of integrity constraints, used to filter the set of candidate explanations.
[edit] Set-cover abduction
A different formalization of abduction is based on inverting the function that calculates the visible effects of the hypotheses. Formally, we are given a set of hypotheses H and a set of manifestations M; they are related by the domain knowledge, represented by a function e that takes as an argument a set of hypotheses and gives as a result the corresponding set of manifestations. In other words, for every subset of the hypotheses  , their effects are known to be e(H').
, their effects are known to be e(H').
Abduction is performed by finding a set  such that
such that 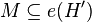 . In other words, abduction is performed by finding a set of hypotheses H' such that their effects e(H') include all observations M.
. In other words, abduction is performed by finding a set of hypotheses H' such that their effects e(H') include all observations M.
A common assumption is that the effects of the hypotheses are independent, that is, for every  , it holds that
, it holds that  . If this condition is met, abduction can be seen as a form of set covering.
. If this condition is met, abduction can be seen as a form of set covering.
[edit] History of the concept
Historically, Aristotle's use of the term epagoge has referred to a syllogism in which the major premise is known to be true, but the minor premise is only probable (Edwards, 1967).
The philosopher Charles Peirce introduced abduction into modern logic. In his works before 1900, he mostly used the term to mean the use of a known rule to explain an observation, e.g., “if it rains the grass is wet” is a known rule used to explain that the grass is wet. In other words, it would be more technically correct to say, "If the grass is wet, the most probable explanation is that it recently rained."
He later used the term to mean creating new rules to explain new observations. Pierce described the process of science as a combination of abduction, deduction and induction, stressing that new knowledge is only created by abduction. This use of 'abduction' is actually most similar to induction. This use is contrary to the common use of abduction in the social sciences and in artificial intelligence, where the old meaning is used. Contrary to this use, Peirce stated that the actual process of generating a new rule is not “hampered” by logic rules. Rather, he pointed out that humans have an innate ability to infer correctly; possessing this ability is explained by the evolutionary advantage it gives.
Norwood Russell Hanson, a philosopher of science, wanted to grasp a logic explaining how scientific discoveries take place. He used Peirce's notion of abduction for this [1].
Further development of the concept can be found in Peter Lipton's "Inference to the Best Explanation" (Lipton, 1991).
[edit] Applications
Applications in artificial intelligence include fault diagnosis, belief revision, and automated planning. The most direct application of abduction is that of automatically detecting faults in systems: given a theory relating faults with their effects and a set of observed effects, abduction can be used to derive sets of faults that are likely to be the cause of the problem.
Abduction can also be used to model automated planning [2]. Given a logical theory relating action occurrences with their effects (for example, a formula of the event calculus), the problem of finding a plan for reaching a state can be modeled as the problem of abducting a set of literals implying that the final state is the goal state.
Belief revision, the process of adapting beliefs in view of new information, is another field in which abduction has been applied. The main problem of belief revision is that the new information may be inconsistent with the corpus of beliefs, while the result of the incorporation cannot be inconsistent. This process can be done by the use of abduction: once an explanation for the observation has been found, integrating it does not generate inconsistency. This use of abduction is not straightforward, as adding propositional formulae to other propositional formulae can only make inconsistencies worse. Instead, abduction is done at the level of the ordering of preference of the possible worlds. Preference models use fuzzy logic or utility models.
In the philosophy of science, abduction has been the key inference method to support scientific realism, and much of the debate about scientific realism is focused on whether abduction is an acceptable method of inference.
In historical linguistics, abduction during language acquisition is often taken to be an essential part of processes of language change such as reanalysis and analogy [3].
[edit] Abductive validation
Abductive validation is the process of validating a given hypothesis through abductive reasoning. This can also be called reasoning through successive approximation. Under this principle, an explanation is valid if it is the best possible explanation of a set of known data. The best possible explanation is often defined in terms of simplicity and elegance (see Occam's razor). Abductive validation is common practice in hypothesis formation in science.
After obtaining results from an inference procedure, we may be left with multiple assumptions, some of which may be contradictory. Abductive validation is a method for identifying the assumptions that will lead to your goal.
[edit] References
- Awbrey, Jon, and Awbrey, Susan (1995), "Interpretation as Action: The Risk of Inquiry", Inquiry: Critical Thinking Across the Disciplines, 15, 40-52. Eprint
- Edwards, Paul (1967, eds.), "The Encyclopedia of Philosophy," Macmillan Publishing Co, Inc. & The Free Press, New York. Collier Macmillan Publishers, London.
- Eiter, T., and Gottlob, G. (1995), "The Complexity of Logic-Based Abduction, Journal of the ACM, 42.1, 3-42.
- Harman, Gilbert (1965). "The Inference to the Best Explanation," The Philosophical Review 74:1, 88-95.
- Josephson, John R., and Josephson, Susan G. (1995, eds.), Abductive Inference: Computation, Philosophy, Technology, Cambridge University Press, Cambridge, UK.
- Lipton, Peter. (2001). Inference to the Best Explanation, London: Routledge. ISBN 0-415-24202-9.
- Menzies, T. (1996), "Applications of Abduction: Knowledge-Level Modeling, International Journal of Human-Computer Studies, 45.3, 305-335.
- Yu, Chong Ho (1994), "Is There a Logic of Exploratory Data Analysis?", Annual Meeting of American Educational Research Association, New Orleans, LA, April, 1994. :Eprint
- Cialdea Mayer, Marta and Pirri, Fiora (1993) "First order abduction via tableau and sequent calculi" Logic Jnl IGPL 1993 1: 99-117; doi:10.1093/jigpal/1.1.99.[1]
- Cialdea Mayer, Marta and Pirri, Fiora (1995) "Propositional Abduction in Modal Logic", Logic Jnl IGPL 1995 3: 907-919; doi:10.1093/jigpal/3.6.907 [2]
[edit] Notes
- ^ Schwendtner, Tibor and Ropolyi, László and Kiss, Olga (eds): Hermeneutika és a természettudományok. Áron Kiadó, Budapest, 2001. It is written in Hungarian. Meaning of the title: Hermeneutics and the natural sciences.
- ^ Kave Eshghi. Abductive planning with the event calculus. In Robert A. Kowalski, Kenneth A. Bowen editors: Logic Programming, Proceedings of the Fifth International Conference and Symposium, Seattle, Washington, August 15-19, 1988. MIT Press 1988, ISBN 0-262-61056-6
- ^ April M. S. McMahon (1994): Understanding language change. Cambridge: Cambridge University Press. ISBN 0-521-44665-1
[edit] See also
- Analogy
- Analysis of Competing Hypotheses
- Charles Peirce
- Charles Peirce (Bibliography)
- Deductive reasoning
- Defeasible reasoning
- Doug Walton
- Gregory Bateson
- Inductive reasoning
- Inquiry
- Maximum likelihood
- List of thinking-related topics
- Logic
- Logical reasoning
- Sign relation
- Scientific method
- Portal:thinking
[edit] External links
- Josephson, John, "Abductive Inference in Reasoning and Perception", Webpage
- Ryder, Martin, Instructional Technology Connections: Abduction, Webpage
- Magnani, Lorenzo, Abduction, Reason, and Science. Processes of Discovery and Explanation, Webpage
- [it] Magnani, Lorenzo
- Chapter 3. Deduction, Induction, and Abduction in article Charles Sanders Peirce of the Stanford Encyclopedia of Philosophy
This article was originally based on material from the Free On-line Dictionary of Computing, which is licensed under the GFDL.

