XOR swap algorithm

From Wikipedia, the free encyclopedia

In computer programming, the XOR swap is an algorithm that uses the XOR bitwise operation to swap distinct values of variables having the same data type without using a temporary variable.

[edit] The algorithm

Standard swapping algorithms require the use of a temporary storage variable. Using the XOR swap algorithm, however, no temporary storage is needed. The algorithm is as follows:

X := X XOR Y
Y := X XOR Y
X := X XOR Y

The algorithm typically corresponds to three machine code instructions. For example, in IBM System/370 assembly code:

XR    R1,R2
XR    R2,R1
XR    R1,R2

where R1 and R2 are registers and each XR operation leaves its result in the register named in the first argument.

However, the problem still remains that if x and y use the same storage location, the value stored in that location will be zeroed out by the first XOR instruction, and then remain zero; it will not be "swapped with itself". (Note that this is not the same as if x and y have the same values. The trouble only comes when x and y use the same storage location.)

[edit] Proof that the XOR swap works

The binary operation XOR over bit strings of length N exhibits the following properties (where 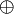denotes XOR):^[1]

• L1. Commutativity:
• L2. Associativity:
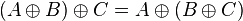
• L3. Identity exists: there is a bit string, 0, (of length N) such that for any A
• L4. Each element is its own inverse: for each A, .

Suppose that we have two distinct registers R1 and R2 as in the table below, with initial values A and B respectively. We perform the operations below in sequence, and reduce our results using the properties listed above.

Step	Operation	Register 1	Register 2	Reduction
0	Initial value			—
1	R1 := R1 XOR R2			—
2	R2 := R1 XOR R2			L2 L4 L3
3	R1 := R1 XOR R2			L1 L2 L4 L3

[edit] Code example

A C function that implements the XOR swap algorithm:

 void xorSwap (int *x, int *y)
 {
     if (x != y) {
         *x ^= *y;
         *y ^= *x;
         *x ^= *y;
     }
 }

Note that the code does not swap the integers passed immediately, but first checks if their memory locations are distinct. This is because the algorithm works only when x and y refer to distinct integers (otherwise, it will erroneously set *x = *y = 0).

The body of this function is sometimes seen incorrectly shortened to if (x != y) *x^=*y^=*x^=*y;. This code has undefined behavior, since it modifies the lvalue *x twice without an intervening sequence point.

[edit] Reasons for use in practice

This article is missing citations or needs footnotes. Please help add inline citations to guard against copyright violations and factual inaccuracies. (July 2008)

In most practical scenarios, the trivial swap algorithm using a temporary register is more efficient. Limited situations in which it may be practical include:

• On a processor where the instruction set encoding permits the XOR swap to be encoded in a smaller number of bytes;
• In a region with high register pressure, it may allow the register allocator to avoid spilling a register.

Because these situations are rare, most optimizing compilers do not generate XOR swap code.

[edit] Reasons for avoidance in practice

Most modern compilers can optimize away the temporary variable in the naive swap, in which case the naive swap uses the same amount of memory and the same number of registers as the XOR swap and is at least as fast, and often faster.^[2] As a general rule, you should never use the XOR swap unless you know for a fact that the naive swap will not suit your application (which is very rare in this day and age). The XOR swap is also much less readable, and can be completely opaque to anyone who isn't already familiar with the technique.

On modern (desktop) CPUs, the XOR technique is considerably slower than using a temporary variable to do swapping. One reason is that modern CPUs strive to execute commands in parallel; see Instruction pipeline. In the XOR technique, the inputs to each operation depend on the results of the previous operation, so they must be executed in strictly sequential order. If efficiency is of tremendous concern, it is advised to test the speeds of both the XOR technique and temporary variable swapping on the target architecture.

[edit] The XCHG instruction

Modern optimizing compilers work by translating the code they are given into an internal flow-based representation which they transform in many ways before producing their machine-code output. These compilers are more likely to recognize and optimize a conventional (temporary-based) swap than to recognize the high-level language statements that correspond to an XOR swap. Many times, what is written as a swap in high-level code is translated by the compiler into a simple internal note that two variables have swapped memory addresses, rather than any amount of machine code. Other times, when the target architecture supports it, the compiler can use a single XCHG (exchange) instruction which performs the swap in a single operation.

An XCHG operation was available as long ago as 1964, on the PDP-6 (where it was called EXCH) and in 1970 on the Datacraft 6024 series (where it was called XCHG). The Intel 8086, released in 1978, also included an instruction named XCHG. All three of these instructions swapped registers with registers, or registers with memory, but were unable to swap the contents of two memory locations. The Motorola 68000's EXG operation can only swap registers with registers. The PDP-10 inherited the PDP-6's EXCH instruction, but the PDP-11 (the machine on which the C programming language was developed) did not.

In modern processors (e.g. x86) the XCHG instruction may impose an implicit LOCK instruction so that the operation is atomic. One wishing to avoid this lock should only use XCHG to swap registers and not memory. However, the ability to atomically swap memory is useful for writing locking primitives used in threaded or multiprocessing applications.

[edit] Aliasing

The XOR swap is also complicated in practice by aliasing. As noted above, if an attempt is made to XOR-swap the contents of some location with itself, the result is that the location is zeroed out and its value lost. Therefore, XOR swapping must not be used blindly in a high-level language if aliasing is possible.

[edit] Variations

The underlying principle of the XOR swap algorithm can be applied to any reversible binary operation. Replacing XOR by addition and subtraction gives a slightly different, but largely equivalent, formulation:

 void addSwap (int *x, int *y)
 {
     if (x != y) {
         *x = *x + *y;
         *y = *x - *y;
         *x = *x - *y;
     }
 }

Unlike the XOR swap, this variation requires that the underlying processor or programming language uses a method such as modular arithmetic or bignums to guarantee that the computation of X + Y cannot cause an error due to integer overflow. Therefore, it is seen even more rarely in practice than the XOR swap.

[edit] Notes

1. ^ The first three properties, along with the existence of an inverse for each element, are the definition of an Abelian group. The last property is a structural feature of XOR not necessarily shared by other Abelian groups, nor groups in general.
2. ^ How to swap two integers in C++: http://big-bad-al.livejournal.com/98093.html

[edit] See also

• Symmetric difference
• XOR linked list