Set theory

From Wikipedia, the free encyclopedia

For the musical concepts, see Set theory (music).

Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics.

The modern study of set theory was initiated by Cantor and Dedekind in the 1870s. After the discovery of paradoxes in informal set theory, numerous axiom systems were proposed in the early twentieth century, of which the Zermelo–Fraenkel axioms, with the axiom of choice, are the best-known.

Set theory, formalized using first-order logic, is the most common foundational system for mathematics. The language of set theory is used in the definitions of nearly all mathematical objects, such as functions, and concepts of set theory are integrated throughout the mathematics curriculum. Elementary facts about sets and set membership can be introduced in primary school, along with Venn diagrams, to study collections of commonplace physical objects. Elementary operations such as set union and intersection can be studied in this context. More advanced concepts such as cardinality are a standard part of the undergraduate mathematics curriculum.

Beyond its use as a foundational system, set theory is a branch of mathematics in its own right, with an active research community. Contemporary research into set theory includes a diverse collection of topics, ranging from the structure of the real number line to the study of the consistency of large cardinals.

[edit] History

See Johnson (1972) for a book-length treatment. Mathematical topics typically emerge and evolve through interactions among many researchers. The point of origin of set theory is somewhat unusual in that it can be identified as an 1874 paper by Georg Cantor: "On a Characteristic Property of All Real Algebraic Numbers".^[1]^[2]^[3]

Beginning with the work of Zeno around 450 BC, mathematicians had been struggling with the concept of infinity. Especially notable is the work of Bernard Bolzano in the first half of the 19th century. The modern understanding of infinity began 1867-71, with Georg Cantor's work on number theory. An 1872 meeting between Cantor and Dedekind much influenced Cantor's thinking and culminated in Cantor (1874)^[1].

Cantor's work initially polarized the mathematicians of his day. While Weierstrass and Dedekind supported Cantor, Kronecker, now seen as a founder of mathematical constructivism, did not. But the utility of Cantorian concepts such as one-to-one correspondence among sets, his proof that there are more real numbers than integers, and the "infinity of infinities" ("Cantor's paradise") the power set operation gives rise to, eventually led to the widespread acceptance of Cantorian set theory.

The next wave of excitement in set theory came around 1900, when it was discovered that Cantorian set theory gave rise to several contradictions, called antinomies or paradoxes. Russell and Zermelo independently found the simplest and best known paradox, now called Russell's paradox and involving "the set of all sets that are not members of themselves." Clearly this set cannot be a member of itself, and hence it must be a member of itself! In 1899 Cantor had himself posed the question: "what is the cardinal number of the set of all sets?" and obtained a related paradox. It was later realized that these paradoxes are not merely set theoretic, and that in logic the sentence "this sentence is false" gives rise to a similar problem, for if the sentence is true, it must be false. Kurt Gödel used this fact in the 1931 proof of his celebrated incompleteness theorem.

The momentum of set theory was such that debate on the paradoxes did not lead to its abandonment. The work of Zermelo in 1908 and Fraenkel in 1922 resulted in the canonical axiomatic set theory ZFC, which is thought to be free of paradoxes. The work of analysts such as Lebesgue demonstrated the great mathematical utility of set theory. Axiomatic set theory has become woven into the very fabric of mathematics as we know it today.

[edit] Basic concepts

Main articles: Set (mathematics) and Algebra of sets

Set theory begins with a fundamental binary relation between an object o and a set A. If o is a member (or element) of A, we write $o \isin A$ .

The basic binary relation between two sets is the subset relation, also called set inclusion. If all the members of set A are also members of set B, then A is a subset of B, denoted 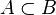$A \subset B$ . For example, {1,2} is a subset of {1,2,3}, but {1,4} is not.

Just as arithmetic features binary operations on numbers, set theory features binary operations on sets. The:

Union of the sets A and B, denoted 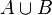$A \cup B$ , is the set whose members are members of at least one of A or B. The union of {1, 2, 3} and {2, 3, 4} is the set {1, 2, 3, 4}.
Intersection of the sets A and B, denoted $A \cap B$ , is the set whose members are members of both A and B. The intersection of {1, 2, 3} and {2, 3, 4} is the set {2, 3}.
Complement of set A relative to set U, denoted $\ A^c$ , is the set of all members of U that are not members of A. This terminology is most commonly employed when U is a universal set, as in the study of Venn diagrams. This operation is also called the set difference of U and A, denoted $U \setminus A.$ The complement of {1,2,3} relative to {2,3,4} is {4}, while, conversely, the complement of {2,3,4} relative to {1,2,3} is {1}.
Symmetric difference of sets A and B is the set whose members are members of exactly one of A and B. For instance, for the sets {1,2,3} and {2,3,4}, the symmetric difference set is {1,4}.
Cartesian product of A and B, denoted 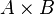$A \times B$ , is the set whose members are all possible ordered pairs (a,b) where a is a member of A and b is a member of B.

The power set of a set A is the set whose members are all possible subsets of A. For example, the powerset of {1, 2} is { {}, {1}, {2}, {1,2} }.

[edit] Some ontology

Main articles: von Neumann universe and Cumulative hierarchy

A set is pure if all of its members are sets, all members of its members are sets, and so on. For example, the set containing only the empty set is a nonempty pure set. When doing set theory, it is common to restrict attention to the pure sets, and many systems of axiomatic set theory are designed to axiomatize the pure sets only.

A key idea in set theory is the von Neumann universe of pure sets. Sets in this universe are arranged in a cumulative hierarchy, based on how deeply their members, members of members, etc. are nested. Each set is assigned an ordinal number α in this hierarchy, known as its rank. A set is assigned a rank by transfinite recursion: if the least upper bound on the ranks of the members of a set X is α then X is assigned rank α+1. Also, for each ordinal α, the set V_α contains all sets assigned a rank no greater than α.

[edit] Axiomatic set theory

Elementary set theory can be studied informally and intuitively, and so can be taught in primary schools using, say, Venn diagrams. The intuitive approach silently assumes that all objects in the universe of discourse satisfying any defining condition form a set. This assumption gives rise to antinomies, the simplest and best known of which being Russell's paradox. Axiomatic set theory was originally devised to rid set theory of such antinomies.

The most widely studied systems of axiomatic set theory imply that all sets form a cumulative hierarchy. Such systems come in two flavors, those whose ontology consists of:

Sets alone. This includes the most common axiomatic set theory, Zermelo–Fraenkel set theory (ZFC), which includes the axiom of choice. Fragments of ZFC include:
- Zermelo set theory, which replaces the axiom schema of replacement with that of separation;
- General set theory, a small fragment of Zermelo set theory sufficient for the Peano axioms and finite sets;
- Kripke-Platek set theory, which omits the axioms of infinity, powerset, and choice, and weakens the axiom schemata of separation and replacement.
Sets and proper classes. This includes Von Neumann-Bernays-Gödel set theory, which has the same strength as ZFC for theorems about sets alone, and Morse-Kelley set theory, which is stronger than ZFC.

For the above systems, allowing urelements (objects that can be members of sets while having no members themselves) does not give rise to any interesting mathematics.

The systems NFU (with urelements) and NF (lacking them) are not based on a cumulative hierarchy. NF and NFU include a "set of all sets," relative to which every set has a complement. Here urelements matter, because NF, but not NFU, allows sets for which the axiom of choice does not hold.

Systems of constructive set theory, such as CST, CZF, and IZF, embed their set axioms in intuitionistic logic instead of first order logic. Yet other systems accept standard first order logic but feature a nonstandard membership relation. These include rough set theory and fuzzy set theory, in which the value of an atomic formula embodying the membership relation is not simply True and False. The Boolean-valued models of ZFC are a related subject.

[edit] Applications

Nearly all mathematical concepts are now defined formally in terms of sets and set theoretic concepts. For example, mathematical structures as diverse as graphs, manifolds, rings, and vector spaces are all defined as sets having various (axiomatic) properties. Equivalence and order relations are ubiquitous in mathematics, and the theory of relations is entirely grounded in set theory.

Set theory is also a promising foundational system for much of mathematics. Since the publication of the first volume of Principia Mathematica, it has been claimed that most or even all mathematical theorems can be derived using an aptly designed set of axioms for set theory, augmented with many definitions, using first or second order logic (see Metamath). For example, properties of the natural and real numbers can be derived within set theory, as each number system can be identified with a set of equivalence classes under a suitable equivalence relation whose field is some infinite set.

Set theory as a foundation for mathematical analysis, topology, abstract algebra, and discrete mathematics is likewise uncontroversial; mathematicians accept that (in principle) theorems in these areas can be derived from the relevant definitions and the axioms of set theory. Few full derivations of complex mathematical theorems from set theory have been formally verified, however, because such formal derivations are often much longer than the natural language proofs mathematicians commonly present. One verification project, Metamath, includes derivations of more than 10,000 theorems starting from the ZFC axioms and using first order logic.

[edit] Areas of study

Set theory is a major area of research in mathematics, with many interrelated subfields.

[edit] Combinatorial set theory

Main article: Infinitary combinatorics

Combinatorial set theory concerns extensions of finite combinatorics to infinite sets. This includes the study of cardinal arithmetic and the study of extensions of Ramsey's theorem such as the Erdos-Rado theorem.

[edit] Descriptive set theory

Main article: Descriptive set theory

Descriptive set theory is the study of subsets of the real line and, more generally, subsets of Polish spaces. It begins with the study of pointclasses in the Borel hierarchy and extends to the study of more complex hierarchies such as the projective hierarchy and the Wadge hierarchy. Many properties of Borel sets can be established in ZFC, but proving these properties hold for more complicated sets requires additional axioms related to determinacy and large cardinals.

The field of effective descriptive set theory is between set theory and recursion theory. It includes the study of lightface pointclasses, and is closely related to hyperarithmetical theory. In many cases, results of classical descriptive set theory have effective versions; in some cases, new results are obtained by proving the effective version first and then extending ("relativizing") it to make it more broadly applicable.

A recent area of research concerns Borel equivalence relations and more complicated definable equivalence relations. This has important applications to the study of invariants in many fields of mathematics.

[edit] Fuzzy set theory

Main article: Fuzzy set theory

In set theory as Cantor defined and Zermelo and Fraenkel axiomatized, an object is either a member of a set or not. In fuzzy set theory this condition was relaxed by Zadeh so an object has a degree of membership in a set, as number between 0 and 1. E.g. the degree of membership of a person in the set of "tall people" is more flexible than a simple yes or no answer and can be a real number such as 0.75.

[edit] Inner model theory

Main article: Inner model theory

An inner model of Zermelo–Fraenkel set theory (ZF) is a transitive class that includes all the ordinals and satisfies all the axioms of ZF. The canonical example is the constructible universe L developed by Gödel. The study of inner models of extensions of ZF is of interest in set theory because it can be used to prove consistency results. For example, it can be shown that regardless whether a model V of ZF satisfies the continuum hypothesis or the axiom of choice, the inner model L constructed inside the original model will satisfy both the continuum hypothesis and the axiom of choice. Thus the assumption that ZF is consistent (has any model whatsoever) implies that ZF together with these two principles is consistent.

The study of inner models is common in the study of determinacy and large cardinals, especially when considering axioms such as the axiom of determinacy that contradict the axiom of choice. Even if a fixed model of set theory satisfies the axiom of choice, it is possible for an inner model to fail to satisfy the axiom of choice. For example, the existence of sufficiently large cardinals implies that there is an inner model satisfying the axiom of determinacy (and thus not satisfying the axiom of choice).^[4]

[edit] Large cardinals

Main article: Large cardinal property

A large cardinal is a cardinal number with an extra property. Many such properties are studied, including inaccessible cardinals, measurable cardinals, and many more. These properties typically imply the cardinal number must be very large, with the existence of a cardinal with the specified property unprovable in Zermelo-Fraenkel set theory.

[edit] Determinacy

Main article: Determinacy

Determinacy refers to the fact that, under appropriate assumptions, certain two-player games of perfect information are determined from the start in the sense that one player must have a winning strategy. The existence of these strategies has important consequences in descriptive set theory, as the assumption that a broader class of games is determined often implies that a broader class of sets will have a topological property. The axiom of determinacy (AD) is an important object of study; although incompatible with the axiom of choice, AD implies that all subsets of the real line are well behaved (in particular, measurable and with the perfect set property). AD can be used to prove that the Wadge degrees have an elegant structure.

[edit] Forcing

Main article: Forcing (mathematics)

Paul Cohen invented forcing while searching for a model of ZFC in which the continuum hypothesis fails. Forcing adjoins to some given model of set theory additional sets in order to create a larger model with properties determined by the construction and the original model. For example, Cohen's construction adjoins additional subsets of the natural numbers without changing any of the cardinal numbers of the original model. Forcing is also one of two methods for proving relative consistency by finitistic methods, the other method being Boolean-valued models.

[edit] Cardinal invariants

Main article: Cardinal invariant

A cardinal invariant is a property of the real line measured by a cardinal number. For example, a well-studied invariant is the smallest cardinality of a collection of meagre sets of reals whose union is the entire real line. These are invariants in the sense that any two isomorphic models of set theory must give the same cardinal for each invariant. Many cardinal invariants have been studied, and the relationships between them are often complex and related to axioms of set theory.

[edit] Set-theoretic topology

Main article: Set-theoretic topology

Set-theoretic topology studies questions of general topology that are set-theoretic in nature or that require advanced methods of set theory for their solution. Many of these theorems are independent of ZFC, requiring stronger axioms for their proof. A famous problem is the normal Moore space question, a question in general topology that was the subject of intense research. The answer to the normal Moore space question was eventually proved to be independent of ZFC.

[edit] Objections to set theory

From set theory's inception, some mathematicians objected to it as a foundation for mathematics, arguing, for example, that it is just a game which included elements of fantasy. The most common objection to set theory, one Kronecker voiced in set theory's earliest years, starts from the constructivist view that mathematics is loosely related to computation. If this view is granted, then the treatment of infinite sets, both in naive and in axiomatic set theory, introduces into mathematics methods and objects that are not computable even in principle. Ludwig Wittgenstein questioned the way Zermelo–Fraenkel set theory handled infinities. Wittgenstein's views about the foundations of mathematics were later criticised by Paul Bernays, and closely investigated by Crispin Wright, among others. In the mid 20th century, Errett Bishop dismissed set theory as "God's mathematics, which we should leave for God to do."

Category theorists have proposed topos theory as an alternative to traditional axiomatic set theory. Topos theory can interpret various alternatives to that theory, such as constructivism, finite set theory, and computable set theory.

[edit] See also

Set theory portal

Mathematics portal

Category theory
List of set theory topics
Musical set theory concerns the application of combinatorics and group theory to music; beyond the fact that it uses finite sets it has nothing to do with mathematical set theory of any kind. In the last two decades, transformational theory in music has taken the concepts of mathematical set theory more rigorously (see Lewin 1987).

[edit] Notes

^ ^a ^b G. Cantor, Über eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen, Crelles Journal f. Mathematik 77 (1874) 258 - 262.
^ Philip Johnson, 1972, A History of Set Theory, Prindle, Weber & Schmidt ISBN 0871501546
^ A History of Set Theory.
^ Jech, Thomas (2003), Set Theory: Third Millennium Edition, Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-44085-7 , p. 642.

[edit] Further reading

Keith Devlin, 1993. The Joy of Sets. Springer Verlag.
Tiles, Mary, 2004 (1989). The Philosophy of Set Theory: An Historical Introduction to Cantor's Paradise. Dover Publications.

[edit] External links

Wikibooks has a book on the topic of

Set Theory