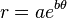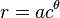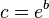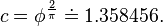Golden spiral
From Wikipedia, the free encyclopedia
 |
|
In geometry, a golden spiral is a logarithmic spiral whose growth factor b is related to φ, the golden ratio.[1] Specifically, a golden spiral gets wider (or further from its origin) by a factor of φ for every quarter turn it makes.
Contents |
[edit] Formula
The polar equation for a golden spiral is the same as for other logarithmic spirals, but with a special value of b:[2]
or
with e being the base of natural logarithms, a being an arbitrary positive real constant, and b such that when θ is a right angle (a quarter turn in either direction):
Therefore, b is given by
The numerical value of b depends on whether the right angle is measured as 90 degrees or as 
radians; and since the angle can be in either direction, it is easiest to write the formula for the absolute value of b (that is, b can also be the negative of this value):
for θ in degrees;
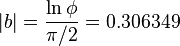for θ in radians.
An alternate formula for a logarithmic and golden spiral is:[3]
where the constant c is given by:
which for the golden spiral gives c values of:
and
[edit] Approximations of the golden spiral
There are several similar spirals that approximate, but do not exactly equal, a golden spiral.[4] These are often confused with the golden spiral.
For example, a golden spiral can be approximated by a "whirling rectangle diagram," in which the opposite corners of squares formed by spiraling golden rectangles are connected by quarter-circles. The result is very similar to a true golden spiral (See image on top right).
Another approximation is a Fibonacci spiral, which is not a true logarithmic spiral. Every quarter turn a Fibonacci spiral gets wider not by φ, but by a changing factor related to the ratios of consecutive terms in the Fibonacci sequence. The ratios of consecutive terms in the Fibonacci series approach φ, so that the two spirals are very similar in appearance. (See image on bottom right).
[edit] Spirals in nature
Approximate logarithmic spirals can occur in nature (for example, the arms of spiral galaxies or sunflower heads). It is sometimes stated that nautilus shells get wider in the pattern of a golden spiral, and hence are related to both φ and the Fibonacci series. In truth, nautilus shells exhibit logarithmic spiral growth, but at a rate distinctly different from that of the golden spiral.[5] The reason for this growth pattern is that it allows the organism to grow at a constant rate without having to change shape. Spirals are common features in nature; golden spirals are but one special case of these.
[edit] References
- ^ "Golden Spiral" by Yu-Sung Chang, The Wolfram Demonstrations Project.
- ^ Priya Hemenway (2005). Divine Proportion: Φ Phi in Art, Nature, and Science. Sterling Publishing Co. pp. 127–129. ISBN 1402735227.
- ^ Klaus Mainzer (1996). Symmetries of Nature: A Handbook for Philosophy of Nature and Science. Walter de Gruyter. pp. 45, 199–200. ISBN 3110129906. http://books.google.com/books?id=rqzaQo6CaA0C&pg=PA200&ots=8airJXF_BB&dq=%22golden+spiral%22+log&as_brr=3&sig=3jQ4u9WBBv-taoGZR8jtu_5Nv9o.
- ^ Charles B. Madden (1999). Fractals in Music: introductory mathematics for musical analysis. High Art Press. pp. 14–16. ISBN 0967172764. http://books.google.com/books?id=JhnERQLm4lUC&dq=rectangles+approximate+golden-spiral.
- ^ Oberon Zell-Ravenheart (2004). Grimoire for the Apprentice Wizard. Career Press. pp. 274. ISBN 1564147118. http://books.google.com/books?id=cMuQADen69UC&pg=PA274&ots=Va2nU5LDpv&dq=nautilus+%22golden+spiral%22&sig=7ZaQ_SaO7bUW86L9s7CqWv68-7M#PPA274,M1.
