Busy beaver

From Wikipedia, the free encyclopedia

In computability theory, a busy beaver (from the colloquial expression for "industrious person") is a Turing machine which, when started on an empty tape, runs as long as possible, but eventually halts. This machine attains the limits on the amount of time and space that a halting Turing machine of the same class can consume.

The busy beaver function quantifies those limits and is an example of a non-computable function. In fact, it can be shown to grow faster than any computable function. The concept was first introduced by Tibor Radó as the "busy beaver game" in his 1962 paper, "On Non-Computable Functions".

[edit] The busy beaver game

In his 1962 paper, Tibor Radó introduces the busy beaver game as follows:

Consider a Turing machine with the binary alphabet {0, 1} and n operational states (often labeled 1, 2, ... n or A, B, C, ...) and an additional Halt state.

His definition of a Turing machine was as follows:

The machine runs on a 2-way infinite (or unbounded) tape.
The machine's transition function takes 2 inputs:

the machine's current state; and
the tape symbol at the current position

and produces 3 outputs:

a symbol to write over the symbol that was read (although, it may be the same as the one that was there);
a direction to move (Left or Right -- "none" is not allowed in this model); and
a state to transition into (which may be the same as the one it was in and may be the halt state).

Thus the Turing machine is of the type whose "program" consists of a finite table of 5-tuples of the form

(current state, current symbol, symbol to write, direction of shift, next state).

The machine halts if and when it reaches the special Halt state.

Now start with a blank tape (i.e. every cell has a 0 in it). Run the machine (by iteratively applying the transition function). If it halts, note the number of 1s it leaves on the tape.

The n-state busy beaver (BB-n) game is a competition to find an n-state Turing machine which leaves the largest number of 1s on its tape before halting.

Rado stated: in order to take part in this competition you must submit the description of an n-state Turing machine that halts along with the number of steps it takes to halt to a qualified umpire who must test its validity. It is important that you provide the number of steps taken to halt, because if you do not and your Turing machine does not halt, there is no general algorithm that the umpire can use to prove that it will not halt. Whereas if you do provide a finite number of steps along with a candidate machine, the umpire can (given enough time) decide whether or not the machine will halt in so many steps. (However, umpires might have difficulty testing current champions for correctness, given the extremely large number of steps taken.)

[edit] The busy beaver function Σ(n)

The busy beaver function Σ(n) is defined as the number of 1s that the champion Turing machine prints given the number n of "states" (Turing-instructions) and a blank tape at the outset.

Radó went on to demonstrate that there is a well-defined champion to the n-state busy beaver Game:

There are a finite number of Turing machines with n states and 2 symbols, specifically there are [4(n+1)]²ⁿ of them [1]. In addition it is trivial that some of these are halting machines; i.e., there exists at least one n-state, 2-symbol TM that will halt, for every n.

Now define:

$E n$ to be the finite, non-empty set of halting $n$ -state, 2-symbol Turing machines of the type described in the preceding section (two-way infinite tape, transition function defined by 5-tuples, etc.).
$σ(M)$ is the number of 1s left on the tape after the Turing machine $M$ is run on a blank tape (defined for all machines $M$ in $E n$ ).
$\Sigma(n) = \max \{ \sigma(M) | M \in E_n \}$ (The largest number of 1s written by any n-state 2-symbol Turing machine)

Since σ(M) is a non-negative finite number for any M halting (in E_n), and since E_n is a non-empty finite set, Σ(n) is a well-defined non-negative finite number for any n.

This Σ is the busy beaver function and any n-state, 2-symbol machine M for which σ(M) = Σ(n) (i.e. which attains the maximum) is called a busy beaver (Note that there may be more than one n-state busy beaver, e.g. if σ(M₁) = σ(M₂) = Σ(n)).

[edit] Non-computability of Σ

Radó went on to prove that there is no computable function that bounds Σ; that is, for any given computable function f, there must be some n (and thus, one can show, infinitely many n), for which f(n)< Σ(n). (A proof is given below.) In particular, Σ is itself non-computable.

Moreover, this implies that it is undecidable by a general algorithm whether a given candidate is a busy beaver champion (for if we could algorithmically determine whether or not a given candidate was champion, we could then determine the appropriate value of Σ simply by listing all candidates and testing them).

Although there is no single algorithm, A, that takes input n and computes Σ(n) (because Σ is not computable), there is an algorithm A_n that "computes" Σ(n) for any natural number n (see computable function#Examples). Furthermore, for sufficiently small n, it is in fact practical to compute specific values of the busy beaver function. For example, it is not hard to show that Σ(0) = 0, Σ(1) = 1, Σ(2) = 4, and with progressively more difficulty it can be shown that Σ(3) = 6 and Σ(4) = 13 (sequence A028444 in OEIS). Σ(n) has not yet been computed for any instance of n > 4, though lower bounds of 4098 and $101439$ have been determined for n = 5 and n = 6 respectively. For n = 12, Dewdney[1984] cites the following rather large lower bound:

$\Sigma(12) \ \ \geq \ \ 6 \ \cdot \ 4096^{4096^{4096^{~.~^{~.~^{~.~^{4096^{4}}}}}}} > 4096 \uparrow \uparrow 166$

where 4096 appears 166 times in the exponential tower, and the tower of exponents is topped by a 4.

[edit] Max shifts function

Shen Lin proved that Σ(3) = 6 in his 1965 paper with Radó, Computer Studies of Turing Machine Problems.

In order to prove this he used another extreme function of halting n-state Turing machines, the maximum shifts function. Define:

s(M) = the number of shifts M makes before halting for any M in E_n
$S(n) = \max \{ s(M) | M \in E_n \}$ (The largest number of shifts made by any n-state 2-symbol Turing machine)

Because these Turing machines are required to have a shift in each and every transition or "step" (including any transition to a Halt state), the max-shifts function is at the same time a max-steps function.

Now, if you know S(n), you can run all n-state Turing machines for S(n) steps sequentially and note a machine which halted with the most 1s on the tape, then you have found a busy beaver and the number of 1s it writes is Σ(n) (because all n-state TMs that halt will have halted in S(n) steps).

Thus, study of the maximum shifts function has been closely linked with study of the busy beaver function.

[edit] Known values

The function values for Σ(n) and S(n) are only known exactly for n < 5. The current 5-state busy beaver champion produces 4,098 1s, using 47,176,870 steps (discovered by Heiner Marxen and Jürgen Buntrock in 1989), but there remain about 40 machines with nonregular behavior which are believed to never halt, but which have not yet been proven to run infinitely. At the moment the record 6-state busy beaver produces over 10¹⁴³⁹ 1s, using over 10²⁸⁷⁹ steps (found by Terry and Shawn Ligocki in 2007). As noted above, these busy beavers are 2-symbol Turing machines.

Milton Green constructed a set of machines demonstrating that

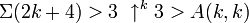$\Sigma(2k+4) > 3\ \uparrow^k 3 > A(k,k)$ (Where $\uparrow$ is Knuth up-arrow notation and A is Ackermann's function)

in his 1964 paper "A Lower Bound on Rado's Sigma Function for Binary Turing Machines". Thus

$\Sigma(10) > 3 \uparrow\uparrow\uparrow 3 = 3 \uparrow\uparrow 3^{3^3} = 3^{3^{3^{.^{.^{.^3}}}}}$ (with

327 = 7,625,597,484,987

terms in the exponential tower)

In contrast, the current bound on Σ(6) is $10^{1439} < 3^{3^{3^3}}$ , tiny in comparison.

[edit] Generalizations

For any model of computation there exist simple analogs of the busy beaver. For example, the generalization to Turing machines with n states and m symbols defines the following generalized busy beaver functions:

Σ(n, m): the largest number of non-zeros printable by an n-state, m-symbol machine started on an initially blank tape before halting, and
S(n, m): the largest number of steps taken by an n-state, m-symbol machine started on an initially blank tape before halting.

For example the longest running 3-state 3-symbol machine found so far runs 119,112,334,170,342,540 steps before halting. The longest running 6-state, 2-symbol machine which has the additional property of reversing the tape value at each step produces 6,147 1s after 47,339,970 steps. So S_RTM(6) ≥ 47,339,970 and Σ_RTM(6) ≥ 6,147.

Likewise we could define an analog to the Σ function for register machines as the the largest number which can be present in any register on halting, for a given number of instructions.

[edit] Applications

In addition to posing a rather challenging mathematical game the busy beaver functions have a profound application. Many open problems in mathematics could be solved in a systematic way given the value of S(n) for a sufficiently large n.^[1]

Consider any conjecture that could be disproven via a counterexample among a countable number of cases (e.g. Goldbach's conjecture). Write a computer program that sequentially tests this conjecture for increasing values (in the case of Goldbach's conjecture, we would consider every even number ≥ 4 sequentially and test whether or not it is the sum of two prime numbers). We will consider this program to be simulated by an n-state Turing machine (although we could alternatively define the busy beaver function for any well-defined programming language). If it finds a counterexample (an even number ≥ 4 that is not the sum of 2 primes in our example), it halts and notifies us. However, if the conjecture is true, then our program will never halt. (This program halts only if it finds a counterexample.)

Now, this program is simulated by an n-state Turing machine, so if we know S(n) we can decide (in a finite amount of time) whether or not it will ever halt by simply running the machine that many steps. And if, after S(n) steps, the machine does not halt, we know that it never will and thus that there are no counterexamples to the given conjecture (i.e., no even numbers that are not the sum of two primes). This would prove the conjecture to be true.

Thus specific values (or upper bounds) for S(n) could be used to systematically solve many open problems in mathematics (in theory). However, current results on the busy beaver problem suggest that this will not be practical for two reasons:

It is extremely hard to prove values for the busy beaver function (and the max shift function). It has only been proven for extremely small machines with less than 5 states, while one would presumably need at least 20-50 states to make a useful machine.
The values of the busy beaver function (and max shift function) get very large, very fast. S(6) > 10²⁸⁷⁹ already requires special pattern-based acceleration to be able to simulate to completion. Likewise, we know that $S(10) > \Sigma(10) > 3 \uparrow\uparrow\uparrow 3$ is a gigantic number. Thus, even if we knew, say, S(30), it may be completely unreasonable to run any machine that number of steps.

[edit] Proof for uncomputability of S(n) and Σ(n)

Suppose that S(n) is a computable function and let EvalS denote a TM, evaluating S(n). Given a tape with n 1s it will produce S(n) 1s on the tape and then halt. Let Clean denote a Turing machine cleaning the sequence of 1s initially written on the tape. Let Double denote a Turing machine evaluating function n + n. Given a tape with n 1s it will produce 2n 1s on the tape and then halt. Let us create the composition Double | EvalS | Clean and let n₀ be the number of states of this machine. Let Create_n₀ denote a Turing machine creating n₀ 1s on an initially blank tape. This machine may be constructed in a trivial manner to have n₀ states (the state i writes 1, moves the head right and switches to state i + 1, except the state n₀, which halts). Let N denote the sum n₀ + n₀.

Let BadS denote the composition Create_n₀ | Double | EvalS | Clean. Notice that this machine has N states. Starting with an initially blank tape it first creates a sequence of n₀ 1s and then doubles it, producing a sequence of N 1s. Then BadS will produce S(N) 1s on tape, and at last it will clear all 1s and then halt. But the phase of cleaning will continue at least S(N) steps, so the time of working of BadS is strictly greater than S(N), which contradicts to the definition of the function S(n).

The uncomputability of Σ(n) may be proved in a similar way. In the above proof, one must exchange the machine EvalS with EvalΣ and Clean with Increment - a simple TM, searching for a first 0 on the tape and replacing it with 1.

The uncomputability of S(n) can also be trivially established by reference to the halting problem. As S(n) is the maximum number of steps that can be performed by a halting Turing machine, any machine which runs for more steps must be non-halting. One could then determine whether a given Turing machine with n states halts by running it for S(n) steps; if it has still not halted, it never will. As being able to compute S(n) would provide a solution to the provably uncomputable halting problem, it follows that S(n) must likewise be uncomputable.

[edit] Examples of busy beaver Turing machines

For an example of a 3-state busy beaver's state table and its "run" see Turing machine examples.

These are tables of rules for the Turing machines that generate Σ(1) and S(1), Σ(2) and S(2), Σ(3) (but not S(3)), Σ(4) and S(4), and the best known lower bound for Σ(5) and S(5), and Σ(6) and S(6).

In the tables, the columns represent the current state and the rows represent the current symbol read from the tape. The table entries indicate the symbol to write onto the tape, the direction to move, and the new state (in that order).

Each machine begins in state A with an infinite tape that contains all 0s. Thus, the initial symbol read from the tape is a 0.

Result Key: (starts at the position underlined, halts at the position in bold)

[edit] 1-state, 2-symbol

	A
0	P1,R,H
1	Never used

Result: 0 0 1 0 0 (1 step, one "1" total)

[edit] 2-state, 2-symbol

	A	B
0	P1,R,B	P1,L,A
1	P1,L,B	P1,R,H

Result: 0 0 1 1 1 1 0 0 (6 steps, four "1"s total)

[edit] 3-state, 2-symbol

	A	B	C
0	P1,R,B	P0,R,C	P1,L,C
1	P1,R,H	P1,R,B	P1,L,A

Result: 0 0 1 1 1 1 1 1 0 0 (14 steps, six "1"s total).

Note that unlike the previous machines, this one is a champion only for Σ, but not for S. (S(3) = 21.)

[edit] 4-state, 2-symbol

	A	B	C	D
0	P1,R,B	P1,L,A	P1,R,H	P1,R,D
1	P1,L,B	P0,L,C	P1,L,D	P0,R,A

Result: 0 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 (107 steps, thirteen "1"s total)

[edit] current 5-state, 2-symbol possible champion

	A	B	C	D	E
0	P1,R,B	P1,R,C	P1,R,D	P1,L,A	P1,R,H
1	P1,L,C	P1,R,B	P0,L,E	P1,L,D	P0,L,A

Result: 4098 "1"s with 8191 "0"s interspersed in 47,176,870 steps.

[edit] current 6-state, 2-symbol best contender

	A	B	C	D	E	F
0	P1,R,B	P1,L,C	P1,L,D	P1,L,E	P1,L,A	P1,L,E
1	P0,L,E	P0,R,A	P0,R,C	P0,L,F	P1,L,C	P1,R,H

Result: ≈4.640 × 10¹⁴³⁹ 1s in ≈2.584 × 10²⁸⁷⁹ steps.

[edit] Exact values and lower bounds for some S(n, m) and Σ(n, m)

The following table lists the exact values and some known lower bounds for S(n, m) and Σ(n, m) for the generalized busy beaver problems. Known exact values are shown as plain integers and known lower bounds are preceded by a greater than or equal to (≥) symbol. Note: entries listed as "???" are bounded from below by the maximum of all entries to left and above. These machines either haven't been investigated or were subsequently surpassed by a machine preceding them.

The Turing machines that achieve these values are available on either Heiner Marxen's and Pascal Michel's WWW pages. Each of these WWW sites also contains some analysis of the Turing machines and references to the proofs of the exact values.

Values of S(n,m):

	2-state	3-state	4-state	5-state	6-state
2-symbol	6	21	107	≥ 47,176,870	≥ 2.5 × 10²⁸⁷⁹
3-symbol	≥ 38	≥ 119,112,334,170,342,540	≥ 1.0 × 10¹⁴⁰⁷²	???	???
4-symbol	≥ 3,932,964	≥ 5.2 × 10¹³⁰³⁶	???	???	???
5-symbol	≥ 1.9 × 10⁷⁰⁴	???	???	???	???
6-symbol	≥ 2.4 × 10⁹⁸⁶⁶	???	???	???	???

Values of Σ(n,m):

	2-state	3-state	4-state	5-state	6-state
2-symbol	4	6	13	≥ 4,098	≥ 4.6 × 10¹⁴³⁹
3-symbol	≥ 9	≥ 374,676,383	≥ 1.3 × 10⁷⁰³⁶	???	???
4-symbol	≥ 2,050	≥ 3.7 × 10⁶⁵¹⁸	???	???	???
5-symbol	≥ 1.7 × 10³⁵²	???	???	???	???
6-symbol	≥ 1.9 × 10⁴⁹³³	???	???	???	???

[edit] See also

Kolmogorov complexity

[edit] Notes

^ Chaitin 1987

[edit] References

Radó, Tibor (1962), On non-computable functions, Bell System Technical Journal, Vol. 41, No. 3 (May 1962), pp. 877-884. This is where Radó first defined the busy beaver problem and proved that it was uncomputable and grew faster than any computable function.
Lin, Shen and Radó, Tibor (1965), Computer Studies of Turing Machine Problems, Journal of the ACM, Vol. 12, No. 2 (April 1965), pp. 196-212. Lin was a doctoral student under Radó. This paper appeared in part of Lin's thesis. Lin proves that Σ(3) = 6 and S(3) = 21 by proving that all 3-state 2-symbol Turing Machines which don't halt after 21 steps will never halt (Most are proven automatically by a computer program, however 40 are proven by human inspection).
Brady, Allen H. (1983), The determination of the value of Rado's noncomputable function Sigma(k) for four-state Turing machines, Mathematics of Computation, Vol. 40, No. 162 (April 1983), pp. 647-665. Brady proves that Σ(4) = 13 and S(4) = 107. Brady defines two new categories for non-halting 3-state 2-symbol Turing Machines: Christmas Trees and Counters. He uses a computer program to prove that all but 27 machines which run over 107 steps are variants of Christmas Trees and Counters which can be proven to run infinitely. The last 27 machines (referred to as holdouts) are proven by personal inspection by Brady himself not to halt.
Machlin, Rona and Stout, Quentin F. (1990), The complex behavior of simple machines, Physica D, No. 42 (June 1990), pp. 85-98. Machlin and Stout describe the busy beaver problem and many techniques used for finding busy beavers (Which they apply to Turing Machines with 4-states and 2-symbols, thus verifying Brady's proof). They use the known values for S for all machines with ≤ 4 states and 2 symbols to estimate a variant of Chaitin's halting probability (Ω).
Marxen, Heiner and Buntrock, Jürgen (1990), Attacking the Busy Beaver 5, Bulletin of the EATCS, No 40 (February 1990), pp. 247-251. Marxen and Buntrock demonstrate that Σ(5) ≥ 4098 and S(5) ≥ 47,176,870 and describe in detail the method they used to find these machines and prove many others will never halt.
Green, Milton W. (1964), A Lower Bound on Rado's Sigma Function for Binary Turing Machines, in Preceedings of the IEEE Fifth Annual Symposium on Switching Circuits Theory and Logical Design, pp. 91-94. Green recursively constructs machines for any number of states and provides the recursive function that computes their score (computes σ), thus providing a lower bound for Σ. This function's growth is comparable to that of Ackermann's function.
Busy beaver programs are described by Alexander Dewdney in Scientific American, August 1984, pages 19-23, also March 1985 p. 23 and April 1985 p. 30.

Dewdney, Alexander K. A computer trap for the busy beaver, the hardest working Turing machine, Scientific American, 251 (2), 10-17, 1984.

Chaitin, Gregory J. (1987), Computing the Busy Beaver Function, In T. M. Cover and B. Gopinath, Open Problems in Communication and Computation, Springer, 1987, pp. 108-112.
Brady, Allen H. (1995), The Busy Beaver Game and the Meaning of Life, p 237-254, appearing in Herken, Rolf (ed)., The Universal Turing Machine: A Half-Century Survey, 2nd edition (1995), Springer-Verlag, Wien New York. Wherein Brady (of 4-state fame) describes some history of the beast and calls its pursuit "The Busy Beaver Game". He describes other games (e.g. cellular automata and Conway's Game of Life). Of particular interest is the "The Busy Beaver Game in Two Dimensions" (p. 247). With 19 references.
Taylor L. Booth, Sequential Machines and Automata Theory, Wiley, New York, 1967. Cf Chapter 9, Turing Machines. A difficult book, meant for electrical engineers and technical specialists. Discusses recursion, partial-recursion with reference to Turing Machines, halting problem. A reference in Booth attributes busy beaver to Rado. Booth also defines Rado's busy beaver problem in "home problems" 3, 4, 5, 6 of Chapter 9, p. 396. Problem 3 is to "show that the busy beaver problem is unsolvable... for all values of n."

[edit] External links

The page of Heiner Marxen, who, with Jürgen Buntrock, found the above-mentioned records for a 5 and 6-state Turing machine.
Pascal Michel's Historical survey of busy beaver results which also contains best results and some analysis.
The page of Penousal Machado's Genetic Beaver Project uses Evolutionary Computation to find new candidates to the busy beaver Problem
Definition of the class RTM - Reversal Turing Machines, simple and strong subclass of the TMs.
The "Millennium Attack" at the Rensselaer RAIR Lab on the busy beaver Problem.
Aaronson, Scott (1999), Who can name the biggest number?
Eric W. Weisstein, Busy Beaver at MathWorld.
Busy Beaver by Hector Zenil, Wolfram Demonstrations Project.

[0] Chaitin 1987

[1]