Linear temporal logic
From Wikipedia, the free encyclopedia
Linear temporal logic (LTL) is a modal temporal logic with modalities referring to time. In LTL, one can encode formulae about the future of paths such as that a condition will eventually be true, that a condition will be true until another fact becomes true, etc.
Contents |
[edit] Syntax
LTL is built up from a set of propositional variables p1,p2,..., the usual logic connectives 
and the following temporal modal operators:
- X for next (N is used synonymously.);
- G for always (globally);
- F for eventually (in the future);
- U for until;
- R for release.
The first three operators are unary, so that X φ is a well-formed formula whenever φ is a well-formed formula. The last two operators are binary, so that φ U ψ is a well-formed formula whenever φ and ψ are well-formed formulas.
[edit] Semantics
An LTL formula can be evaluated over an infinite sequence of truth evaluations and a position on that path. An LTL formula is satisfied by a path if and only if it is satisfied for position 0 on that path. The semantics for the modal operators is given as follows.
| Textual | Symbolic | Explanation | Diagram |
|---|---|---|---|
| Unary operators: | |||
| X φ |  |
neXt: φ has to hold at the next state. |  |
| G φ |  |
Globally: φ has to hold on the entire subsequent path. |  |
| F φ |  |
Finally: φ eventually has to hold (somewhere on the subsequent path). |  |
| Binary operators: | |||
| ψ U φ |  |
Until: φ holds at the current or a future position, and ψ has to hold until that position. At that position ψ does not have to hold necessarily any more. |  |
| ψ R φ |  |
Release: φ is true until the first position in which ψ is true, or forever if such a position does not exist. | 
|
One can take just two of those operators to be fundamental, and define the others in terms of them, since the following are always satisfied:
- F φ = true U φ
- G φ = false R φ =
F φ - ψ R φ = (ψ U φ)
[edit] Nonstandard connectives
Some authors also define a weak until binary operator, denoted W, with semantics similar to that of the until operator but the stop condition is not required to occur (similar to release). It is sometimes useful since both U and R can be defined in terms of the weak until:
- ψ U φ = F φ
(ψ W φ) - ψ R φ = φ W (ψφ)
- φ W ψ = ψ R (ψ
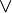φ) - φ W ψ = (φ U ψ)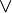G φ
[edit] Important properties
There are two main types of properties that can be expressed using linear temporal logic: safety properties usually state that something bad never happens (Gφ), while liveness properties state that something good keeps happening (GFψ or G
Fψ)). More generally: Safety properties are those for which every counterexample has a finite prefix such that, however it is extended to an infinite path, it is still a counterexample. For liveness properties, on the other hand, every finite prefix of a counterexample can be extended to an infinite path that satisfies the formula.
[edit] Relations with other logics
LTL can be shown to be equivalent to the first-order logic over the smaller relation, FO[<] as well as star-free regular expressions or deterministic finite automata with loop complexity 0.
[edit] Automata theoretic Linear temporal logic model checking
An important way to model check is to express desired properties (such as the ones described above) using LTL operators and actually check if the model satisfies this property. One technique is to obtain a Büchi automaton that is "equivalent" to the model and one that is "equivalent" to the negation of the property. The intersection of the two non-deterministic Büchi automata is empty if the model satisfies the property.
[edit] See also
- Temporal logic in finite-state verification
- Computational tree logic (CTL)
- CTL*
- Interval temporal logic (ITL)
- Büchi automaton
- Reo Coordination Language
