Logical connective
From Wikipedia, the free encyclopedia
In logic, two sentences (either in a formal language or a natural language) may be joined by means of a logical connective to form a compound sentence (Enderton 2001:45). The truth value of the compound is uniquely determined by the truth values of the simpler sentences. Each logical connective therefore represents a function, called a truth function. For this reason, logical connectives are sometimes called truth-functional connectives.
The logical connectives commonly used in mathematics include conjunction (AND), disjunction (OR), and implication.
[edit] Truth functions in natural languages
In the grammar of natural languages two sentences may be joined by a grammatical conjunction to form a grammatically compound sentence. Some but not all such grammatical conjunctions are truth-functions. For example consider the following sentences:
- A: Jack went up the hill.
- B: Jill went up the hill.
- C: Jack went up the hill and Jill went up the hill.
- D: Jack went up the hill so Jill went up the hill.
The words and and so are both grammatical conjunctions joining the sentences (A) and (B) to form the compound sentences (C) and (D). The and in (C) is a logical connective, since the truth of (C) is completely determined by (A) and (B): it would make no sense to affirm (A) and (B) but deny (C). However so in (D) is NOT a logical connective, since it would be quite reasonable to affirm (A) and (B) but deny (D): perhaps, after all, Jill went up the hill fetch a pail of water, not because Jack had gone up the Hill at all. Thus and is a logical connective but so is not.
Various English words and word pairs express truth-functions, and some of them are synonymous. Examples (with the name of the relationship in parentheses) are:
- "and" (conjunction)
- "or" (inclusive or exclusive disjunction)
- "implies" (implication)
- "if...then" (implication)
- "if and only if" (equivalence)
- "only if" (implication)
- "just in case" (equivalence)
- "but" (conjunction)
- "however" (conjunction)
- "not both" (NAND)
- "neither...nor" (NOR)
The word "not" (negation) and "it is false that" (negation) "it is not the case that" (negation) are also English words expressing a logical connective, even though they are applied to a single statement, and do not connect two statements.
[edit] Truth functions in formal languages
In formal languages truth-functions are represented by unambiguous symbols, and these can be exactly defined by means of truth tables. There are 16 binary truth tables, and so 16 different logical connectives which connect exactly two statements, can be defined. Not all of them are in common use. These symbols are called "truth-functional connectives", "logical connectives", "logical operators" or "propositional operators". See well-formed formula for the rules which allow new well-formed formulas to be constructed by joining other well-formed formulas using truth-functional connectives.
Logical connectives can be used to link more than two statements. A more technical definition is that an "n-ary logical connective" is a function which assigns truth values "true" or "false" to n-tuples of truth values.
[edit] Examples
Commonly used logical connectives include:
- Negation (not) (¬ or ~)
- Conjunction (and) (
 or &)
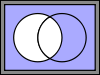
or &) - Disjunction (or) (
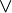 )
) - Material implication (if...then) (
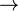 ,
, 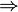 or
or  )
) - Biconditional (if and only if) (xnor) (
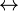 ,
,  , or = )
, or = )
For example, the statements it is raining and I am indoors can be reformed using various different connectives to form sentences that relate the two in ways which augment their meaning:
- It is raining and I am indoors.
- If it is raining then I am indoors.
- It is raining if I am indoors.
- It is raining if and only if I am indoors.
- It is not raining.
If we write 'P' for It is raining and 'Q' for I am indoors and we use the usual symbols for logical connectives, then the above examples could be represented in symbols, respectively:
- P & Q
- P
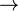 Q
Q - Q
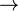 P
P - P
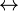 Q
Q - ¬P
[edit] All binary logical connectives
There are sixteen different Boolean functions, associating the inputs P and Q with four digit binary outputs.
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
[edit] Functional completeness
Not all of these operators are necessary for a functionally complete logical calculus. Certain compound statements are logically equivalent. For example, ¬P ∨ Q is logically equivalent to P → Q;. So the conditional operator "→" is not necessary if you have "¬" (not) and "∨" (or).
The smallest set of operators which still expresses every statement which is expressible in the propositional calculus is called a minimal functionally complete set. A minimally complete set of operators is achieved by NAND alone { ↑ } and NOR alone { ↓ }.
The following are the functionally complete sets (of cardinality not exceeding 2) of operators whose arities do not exceed 2:
{ ↓ }, { ↑ }, { 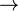 ,
,  }, {
}, { 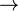 ,
,  }, {
}, {  , ⊂ }, {
, ⊂ }, { 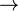 , ⊄ }, {
, ⊄ }, { 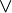 ,
,  }, {
}, { 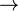 , ⊅ }, { ⊄,
, ⊅ }, { ⊄,  }, { ⊂,
}, { ⊂,  }, { ⊅,
}, { ⊅,  }, { ⊂, ⊄ }, {
}, { ⊂, ⊄ }, {  ,
,  }, { ⊂, ⊅ }, {
}, { ⊂, ⊅ }, {  ,
, 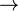 }, { ⊄,
}, { ⊄, 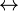 }, { ⊅,
}, { ⊅, 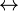 }
}
[edit] Truth functions and interpretation function
Instead of using truth tables, logical connective symbols can be interpreted by means of an interpretation function and a functionally complete set of truth-functions (Gamut 1991). Let I be an interpretation function, let Φ, Ψ be any two sentences and let the truth function fnand be defined as:-
- fnand(T,T)=F; fnand(T,F)=fnand(F,T)=fnand(F,F)=T
Then, for convenience, we define fnot, for fand etc. by means of fnand:-
- fnot(x)=fnand(x,x)
- for(x,y)= fnand(fnot(x), fnot(y))
- fand(x,y)=fnot(fnand(x,y))
or, alternatively we define fnot, for fand, etc directly:-
- fnot(T)=F; fnot(F)=T;
- for(T,T)=for(T,F)=for(F,T)=T;for(F,F)=F
- fand(T,T)=T; fand(T,F)=fand(F,T)=fand(F,F)=F
Then
- I(~)=I(¬)=fnot
- I(&)=I(^)=I(&)=fand
- I(v)=I(
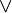 )= for
)= for - I(~Φ)=I(¬Φ=I¬(I(Φ)=fnot(I(Φ))
- I(Φ&Ψ) = I(&)(I(Φ), I(Ψ))= fand(I(Φ), I(Ψ))
etc.
Thus if s is a sentence that is a string of symbols consisting of logical symbols v1..vn representing logical connectives, and non-logical symbols c1..cn , then if and only if I(v1)..I(vn) have been provided interpreting v1 to vn by means of fnand (or any other set of functional complete truth-functions) then the truth-value of I(s) is determined entirely by the truth-values of c1..cn, i.e. of I(c1)..I(cn). In other words, as expected and required, S is true or false only under an interpretation of all its non-logical symbols.
[edit] Properties
The logical connectives each possess different set of properties which may be expressed in the theorems containing the connective. Some of those properties that a logical connective may have are:
- Associativity: Within an expression containing two or more of the same associative connectives in a row, the order of the operations does not matter as long as the sequence of the operands is not changed.
- Commutivity: The operands of the connective may be swapped without affecting the truth-value of the expression.
- Distributivity: A connective denoted by · distributes over another connective denoted by +, if a · (b + c) = (a · b) + (a · c) for all operands a, b, c.
- Idempotency: Whenever the operands of the operation are the same, the connective gives the operand as the result.
- Absorption: A pair of conenctives
 ,
, 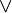 satisfies the absorption law if
satisfies the absorption law if  for all operands a, b.
for all operands a, b.
A set of operators is functionally complete if and only if for each of the following five properties it contains at least one member lacking it:
- monotonic: If f(a1, ..., an) ≤ f(b1, ..., bn) for all a1, ..., an, b1, ..., bn ∈ {0,1} such that a1 ≤ b1, a2 ≤ b2, ..., an ≤ bn. E.g.,
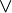 ,
,  ,
,  ,
,  .
. - affine: Each variable always makes a difference in the truth-value of the operation or it never makes a difference. E.g.,
 ,
, 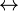 ,
,  ,
,  ,
,  .
. - self dual: To read the truth-value assignments for the operation from top to bottom on its truth table is the same as taking the complement of reading it from bottom to top, in other words f(¬a1, ..., ¬an) = ¬f(a1, ..., an). E.g.,
 .
. - truth-preserving: The interpretation under which all variables are assigned a truth value of 'true' produces a truth value of 'true' as a result of these operations. E.g.,
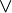 ,
,  ,
,  ,
, 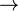 ,
, 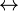 , ⊂.
, ⊂. - falsehood-preserving: The interpretation under which all variables are assigned a truth value of 'false' produces a truth value of 'false' as a result of these operations. E.g.,
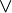 ,
,  ,
,  ,
,  , ⊄, ⊅.
, ⊄, ⊅.
[edit] Arity
In two-valued logic there are 2 nullary operators (constants), 4 unary operators, 16 binary operators, 256 ternary operators, and 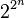 n-ary operators. In three valued logic there are 3 nullary operators (constants), 27 unary operators, 19683 binary operators, 7625597484987 ternary operators, and
n-ary operators. In three valued logic there are 3 nullary operators (constants), 27 unary operators, 19683 binary operators, 7625597484987 ternary operators, and 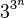 n-ary operators. An n-ary operator in k-valued logic is a function from
n-ary operators. An n-ary operator in k-valued logic is a function from  . Therefore the number of such operators is
. Therefore the number of such operators is  , which is how the above numbers were derived.
, which is how the above numbers were derived.
However, some of the operators of a particular arity are actually degenerate forms that perform a lower-arity operation on some of the inputs and ignores the rest of the inputs. Out of the 256 ternary boolean operators cited above,  of them are such degenerate forms of binary or lower-arity operators, using the inclusion-exclusion principle. The ternary operator
of them are such degenerate forms of binary or lower-arity operators, using the inclusion-exclusion principle. The ternary operator 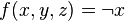 is one such operator which is actually a unary operator applied to one input, and ignoring the other two inputs.
is one such operator which is actually a unary operator applied to one input, and ignoring the other two inputs.
"Not" is a unary operator, it takes a single term (¬P). The rest are binary operators, taking two terms to make a compound statement (P  Q, P
Q, P 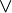 Q, P → Q, P ↔ Q).
Q, P → Q, P ↔ Q).
The set of logical operators 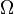 may be partitioned into disjoint subsets as follows:
may be partitioned into disjoint subsets as follows:
In this partition,  is the set of operator symbols of arity
is the set of operator symbols of arity 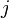 .
.
In the more familiar propositional calculi, 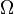 is typically partitioned as follows:
is typically partitioned as follows:
-
-
- nullary operators:

- nullary operators:
-
-
-
- unary operators:

- unary operators:
-
-
-
- binary operators:

- binary operators:
-
[edit] Order of precedence
As a way of reducing the number of necessary parentheses, one may introduce precedence rules: ¬ has higher precedence than ∧, ∧ higher than ∨, and ∨ higher than →. So for example, P ∨ Q ∧ ¬R → S is short for (P ∨ (Q ∧ (¬R))) → S.
Here is a table that shows a commonly used precedence of logical operators.
-
Operator Precedence ¬ 1 ∧ 2 ∨ 3 → 4 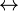
5
The order of precedence determines which connective is the "main connective" when interpreting a non-atomic formula.
[edit] Applications in computer science
Logical operators are implemented as logic gates in digital circuits. Practically all digital circuits (the major exception is DRAM) are built up from NAND, NOR, NOT, and transmission gates. NAND and NOR gates with 3 or more inputs rather than the usual 2 inputs are fairly common, although they are logically equivalent to a cascade of 2-input gates. All other operators are implemented by breaking them down into a logically equivalent combination of 2 or more of the above logic gates.
The "logical equivalence" of "NAND alone", "NOR alone", and "NOT and AND" is similar to Turing equivalence.
Is some new technology (such as reversible computing, clockless logic, or quantum dots computing) "functionally complete", in that it can be used to build computers that can do all the sorts of computation that CMOS-based computers can do? If it can implement the NAND operator, only then is it functionally complete.
That fact that all logical connectives can be expressed with NOR alone is demonstrated by the Apollo guidance computer.
[edit] See also
[edit] References
- Enderton, Herbert (2001), A mathematical introduction to logic (2nd ed.), Boston, MA: Academic Press, ISBN 978-0-12-238452-3
- Gamut, L.T.F (1991). "2". Logic, languagage and Meaning,. 1: Introduction to Logic. University of Chicago Press. pp. 54..64. ISBN 0-226-28285-3.
[edit] External links
- John MacFarlane (2005), "Logical constants", Stanford Encyclopedia of Philosophy.
- Cullinane, Steven H. (2007) "The geometry of logic."
|
|||||||||||||||||||


 ¬Q
¬Q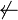 Q
Q ¬Q
¬Q

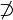 Q
Q


 Q
Q
 Q
Q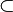 Q
Q


 Q
Q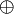 Q
Q






