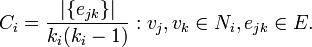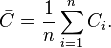Clustering coefficient

From Wikipedia, the free encyclopedia

Example clustering coefficient on an undirected graph for the shaded node

i

. Black line segments are actual edges connecting neighbors of

i

, and dotted red segments are missing edges.

The clustering coefficient of a vertex in a graph quantifies how close the vertex and its neighbors are to being a clique (complete graph). Duncan J. Watts and Steven Strogatz introduced the measure in 1998 ^[1] to determine whether a graph is a small-world network.

[edit] Formal Definition

A graph $G = (V, E)$ formally consists of a set of vertices $V$ and a set of edges $E$ between them. An edge $e i j$ connects vertex $i$ with vertex $j$ .

The neighbourhood N for a vertex $v i$ is defined as its immediately connected neighbours as follows:

$N_i = \{v_j : e_{ij} \in E \and e_{ji} \in E\}.$

The degree $k i$ of a vertex is defined as the number of vertices, $| N i |$ , in its neighbourhood $N i$ .

The clustering coefficient $C i$ for a vertex $v i$ is then given by the proportion of links between the vertices within its neighbourhood divided by the number of links that could possibly exist between them. For a directed graph, $e i j$ is distinct from $e j i$ , and therefore for each neighbourhood $N i$ there are $k i (k i - 1)$ links that could exist among the vertices within the neighbourhood ( $k i$ is the total (in + out) degree of the vertex). Thus, the clustering coefficient for directed graphs is given as

$C_i = \frac{|\{e_{jk}\}|}{k_i(k_i-1)} : v_j,v_k \in N_i, e_{jk} \in E.$

An undirected graph has the property that $e i j$ and $e j i$ are considered identical. Therefore, if a vertex $v i$ has $k i$ neighbours, 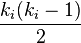$\frac{k_i(k_i-1)}{2}$ edges could exist among the vertices within the neighbourhood. Thus, the clustering coefficient for undirected graphs can be defined as

$C_i = \frac{2|\{e_{jk}\}|}{k_i(k_i-1)} : v_j,v_k \in N_i, e_{jk} \in E.$

Let $λ G (v)$ be the number of triangles on $v \in V(G)$ for undirected graph $G$ . That is, $λ G (v)$ is the number of subgraphs of $G$ with 3 edges and 3 vertices, one of which is $v$ . Let $τ G (v)$ be the number of triples on $v \in G$ . That is, $τ G (v)$ is the number of subgraphs (not necessarily induced) with 2 edges and 3 vertices, one of which is $v$ and such that $v$ is incident to both edges. Then we can also define the clustering coefficient as

$C_i = \frac{\lambda_G(v)}{\tau_G(v)}.$

It is simple to show that the two preceding definitions are the same, since

$\tau_G(v) = C({k_i},2) = \frac{1}{2}k_i(k_i-1).$

These measures are 1 if every neighbour connected to $v i$ is also connected to every other vertex within the neighbourhood, and 0 if no vertex that is connected to $v i$ connects to any other vertex that is connected to $v i$ .

The clustering coefficient for the whole system is given by Watts and Strogatz as the average of the clustering coefficient for each vertex:

$\bar{C} = \frac{1}{n}\sum_{i=1}^{n} C_i.$

A graph is considered small-world, if its average clustering coefficient 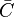$\bar{C}$ is significantly higher than a random graph constructed on the same vertex set, and if the graph has a short mean-shortest path length.