Hoare logic
From Wikipedia, the free encyclopedia
| The introduction to this article provides insufficient context for those unfamiliar with the subject. Please help improve the article with a good introductory style. |
Hoare logic (also known as Floyd–Hoare logic) is a formal system developed by the British computer scientist C. A. R. Hoare, and subsequently refined by Hoare and other researchers. The purpose of the system is to provide a set of logical rules in order to reason about the correctness of computer programs with the rigour of mathematical logic.
It was published in Hoare's 1969 paper,[1] where Hoare acknowledges earlier contributions from Robert Floyd, who had published a similar system[2] for flowcharts.
The central feature of Hoare logic is the Hoare triple. A triple describes how the execution of a piece of code changes the state of the computation. A Hoare triple is of the form
where P and Q are assertions and C is a command. P is called the precondition and Q the postcondition: if the precondition is met, the command establishes the postcondition. Assertions are formulas in predicate logic.
Hoare logic has axioms and inference rules for all the constructs of a simple imperative programming language. In addition to the rules for the simple language in Hoare's original paper, rules for other language constructs have been developed since then by Hoare and many other researchers. There are rules for concurrency, procedures, jumps, and pointers.
Contents |
[edit] Partial and total correctness
Standard Hoare logic proves only partial correctness, while termination would have to be proved separately. Thus the intuitive reading of a Hoare triple is: Whenever P holds of the state before the execution of C, then Q will hold afterwards, or C does not terminate. Note that if C does not terminate, then there is no "after", so Q can be any statement at all. Indeed, one can choose Q to be false to express that C does not terminate.
Total correctness can also be proven with an extended version of the While rule.
[edit] Rules
[edit] Empty statement axiom schema
[edit] Assignment axiom schema
The assignment axiom states that after the assignment any predicate holds for the variable that was previously true for the right-hand side of the assignment:
Here P[x / E] denotes the expression P in which all free occurrences of the variable x have been replaced with the expression E.
The meaning of the assignment axiom is that the truth of {P[x / E]} is equivalent to the after-assignment truth of {P}. Thus if {P[x / E]} were true prior to the assignment, by the assignment axiom then {P} will be true subsequent to that assignment. Conversely, if {P[x / E]} were false prior to the assignment statement, {P} must then be false following the assignment.
Examples of valid triples include:
The assignment axiom proposed by Hoare does not apply when more than one name can refer to the same stored value. For example,
is not a true statement if x and y refer to the same variable, because no precondition can cause y to be 3 after x is set to 2.
[edit] Rule of composition
Hoare's rule of composition applies to sequentially-executed programs S and T, where S executes prior to T and is written S;T.
For example, consider the following two instances of the assignment axiom:
and
By the sequencing rule, one concludes:
[edit] Conditional rule
[edit] Consequence rule
[edit] While rule
Here P is the loop invariant.
[edit] While rule for total correctness
In this rule, in addition to maintaining the loop invariant, one also proves termination by way of a term, called the loop variant, here t, whose value strictly decreases with respect to a well-founded relation during each iteration. Note that, given the invariant P, the condition B must imply that t is not a minimal element of its range, for otherwise the premise of this rule would be false. Because the relation "<" is well-founded, each step of the loop is counted by decreasing members of a finite chain. Also note that square brackets are used here instead of curly braces to denote total correctness, i.e. termination as well as partial correctness. (This is one of various notations for total correctness.)
[edit] Examples
-
Example 1 


(Assignment Axiom) 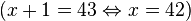


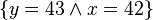
(Consequence Rule) Example 2 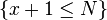

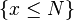
(Assignment Axiom) ( 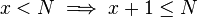 for x, N with integer types.)
for x, N with integer types.)

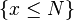
(Consequence Rule)
[edit] See also
- Design by contract
- Dynamic logic
- Edsger W. Dijkstra
- Predicate transformer semantics
- Program verification
- Static code analysis
- Loop invariant
- Refinement calculus
[edit] References
- ^ C. A. R. Hoare. "An axiomatic basis for computer programming". Communications of the ACM, 12(10):576–580,583 October 1969. doi:10.1145/363235.363259
- ^ R. W. Floyd. "Assigning meanings to programs." Proceedings of the American Mathematical Society Symposia on Applied Mathematics. Vol. 19, pp. 19–31. 1967.
[edit] Further reading
- Robert D. Tennent. Specifying Software (a textbook that includes an introduction to Hoare logic, written in 2002) ISBN 0-521-00401-2
[edit] External links
- Project Bali has defined Hoare logic-style rules for a subset of the Java programming language, for use with the Isabelle theorem prover
- KeY-Hoare is a semi-automatic verification system built on top of the KeY theorem prover. It features a Hoare calculus for a simple while language.
- j-Algo-modul Hoare calculus — A visualisation of the Hoare calculus in the in the algorithm visualisation program j-Algo


![\frac{}{\{P[x/E]\}\ x:=E \ \{P\} } \!](http://upload.wikimedia.org/math/5/8/d/58d7aa050f990fc80469c4d0a4d3417c.png)



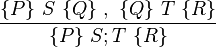
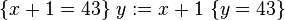

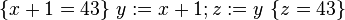
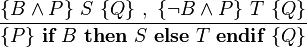


![\frac { <\;\textrm{is\ well-founded,}\;[P \wedge B \wedge t = z ]\ S\ [P \wedge t < z ]}
{ [P]\ \textbf{while}\ B\ \textbf{do}\ S\ \textbf{done}\ [\neg B \wedge P] }
\!](http://upload.wikimedia.org/math/6/5/c/65c99e3ec2d0be62261bc5e0684f0df7.png)

