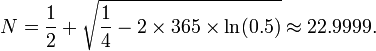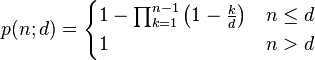Birthday problem

From Wikipedia, the free encyclopedia

In probability theory, the birthday problem, or birthday paradox^[1] pertains to the probability that in a set of randomly chosen people some pair of them will have the same birthday. In a group of at least 23 randomly chosen people, there is more than 50% probability that some pair of them will both have been born on the same day. For 57 or more people, the probability is more than 99%, and it reaches 100% when the number of people reaches 367 (there are a maximum of 366 possible birthdays). The mathematics behind this problem leads to a well-known cryptographic attack called the birthday attack.

A graph showing the approximate probability of at least two people sharing a birthday amongst a certain number of people.

[edit] Understanding the problem

The birthday problem asks whether any of the 23 people have a matching birthday with any of the others — not one in particular. (See "Same birthday as you" below for an analysis of this much less surprising alternative problem.)

In a list of 23 people, comparing the birthday of the first person on the list to the others allows 22 chances for a matching birthday, but comparing every person to all of the others allows 253 distinct chances: in a group of 23 people there are 23×22/2 = 253 pairs. The approximate probability that two people chosen from the entire population at random have the same birthday is 1/365 (ignoring Leap Day, February 29), and presuming all birthdays are equally probable.^[2] Although the pairings in a group of 23 people are not statistically equivalent to 253 pairs chosen independently, the birthday paradox becomes less surprising if a group is thought of in terms of the number of possible pairs, rather than the number of individuals.

[edit] Calculating the probability

To compute the approximate probability that in a room of n people, at least two have the same birthday, we disregard variations in the distribution, such as leap years, twins, seasonal or weekday variations, and assume that the 365 possible birthdays are equally likely. Real-life birthday distributions are not uniform since not all dates are equally likely.^[3]

It is easier to first calculate the probability p(n) that all n birthdays are different. If n > 365, by the pigeonhole principle this probability is 0. On the other hand, if n ≤ 365, it is

$\bar p(n) = 1 \times \left(1-\frac{1}{365}\right) \times \left(1-\frac{2}{365}\right) \cdots \left(1-\frac{n-1}{365}\right) = { 365 \times 364 \cdots (365-n+1) \over 365^n } = { 365! \over 365^n (365-n)!}$

because the second person cannot have the same birthday as the first (364/365), the third cannot have the same birthday as the first two (363/365), etc.

The event of at least two of the n persons having the same birthday is complementary to all n birthdays being different. Therefore, its probability p(n) is

$p(n) = 1 - \bar p(n) .$

The approximate probability that no two people share a birthday in a group of n people.

This probability surpasses 1/2 for n = 23 (with value about 50.7%). The following table shows the probability for some other values of n (This table ignores the existence of leap years, as described above):

n	p(n)
10	11.7%
20	41.1%
23	50.7%
30	70.6%
50	97.0%
57	99.0%
100	99.99997%
200	99.9999999999999999999999999998%
300	(100 − (6×10⁻⁸⁰))%
350	(100 − (3×10⁻¹²⁹))%
367	100%

In Python, these probabilities can be calculated with the following function:

 def bp(n, d):
     v = 1.0
     for i in range(n):
         v = v * (1 - float(i)/d)
     return 1 - v
 
 for n in [22, 23, 56, 57]:
     print "# samples = %i; prob. collision = %f" % (n, bp(n, 365))

[edit] Approximations

The Taylor series expansion of the exponential function

$e^x = 1 + x + \frac{x^2}{2!}+\cdots$

A graph showing the accuracy of the approximation $1-e^{-n^2/(2 \times 365)}$

provides a first-order approximation for e^x:

$e^x \approx 1 + x$

The first expression derived for p(n) can be approximated as

$\begin{align} \bar p(n) & \approx 1 \times e^{-1/365} \times e^{-2/365} \cdots e^{-(n-1)/365} \\ & = 1 \times e^{-(1+2+ \cdots +(n-1))/365} \\ & = e^{-(n(n-1)/2) / 365}. \end{align}$

Therefore,

$p(n) = 1-\bar p(n) \approx 1 - e^{- n(n-1)/(2 \times 365)}.$

An even coarser approximation is given by

$p(n)\approx 1-e^{- n^2/(2 \times 365)},\,$

which, as the graph illustrates, is still fairly accurate.

[edit] A simple exponentiation

The probability of any two people not having the same birthday is 364/365. In a room of people of size N, there are C(N, 2) pairs of people, i.e. C(N, 2) events. The probability of no two people sharing the same birthday can be approximated by assuming that these events are independent and hence by multiplying their probability together. In short 364/365 can be multiplied by itself C(N, 2) times, which gives us

$\left(\frac{364}{365}\right)^{C(N,2)}.$

And if this is the probability of no one having the same birthday, then the probability of someone sharing a birthday is

$p(n) \approx 1 - \left(\frac{364}{365}\right)^{C(N,2)}.$

[edit] Poisson approximation

Using the Poisson approximation for the binomial,

$\mathrm{Poi}\left(\frac{C(23, 2)}{365}\right) =\mathrm{Poi}\left(\frac{253}{365}\right) \approx \mathrm{Poi}(0.6932)$

$\Pr(X>0)=1-\Pr(X=0)=1-e^{-0.6932}=1-0.499998=0.500002.$

Again, this is over 50%.

[edit] Approximation of number of people

This can also be approximated using the following formula for the number of people necessary to have at least a 50% chance of matching:

$N = \frac{1}{2} + \sqrt{\frac{1}{4} - 2 \times 365 \times \ln(0.5)} \approx 22.9999.$

This is a result of the good approximation that an event with 1 in k probability will have a 50% chance of occurring at least once if it is repeated k ln 2 times.^[4]

[edit] An upper bound

The argument below is adapted from an argument of Paul Halmos.^[5]

As stated above, the probability that no two birthdays coincide is

$1-p(n) = \bar p(n) = \prod_{k=1}^{n-1}\left(1-{k \over 365}\right) .$

This can be seen by first counting the number of ways 365 birthdays can be distributed among n people in such a way that no two birthdays are the same, then dividing by the total number of ways 365 birthdays can be distributed among n people:

$\bar p(n) = \dfrac{365\cdot364\cdots(365-n+1)}{365^n}.$

Interest lies in the smallest n such that p(n) > 1/2; or equivalently, the smallest n such that p(n) < 1/2.

Replacing 1 − k/365, as above, with e^−k/365, and using the inequality 1 − x < e^−x, we have

$\bar p(n) = \prod_{k=1}^{n-1}\left(1-{k \over 365}\right) < \prod_{k=1}^{n-1}\left(e^{-k/365}\right) = e^{-(n(n-1))/(2\times 365)} .$

Therefore, the expression above is not only an approximation, but also an upper bound of p(n). The inequality

$e^{-(n(n-1))/(2\cdot 365)} < \frac{1}{2}$

implies p(n) < 1/2. Solving for n we find

$n^2-n > 2\times365\ln 2 \,\! .$

Now, 730 ln 2 is approximately 505.997, which is barely below 506, the value of n² − n attained when n = 23. Therefore, 23 people suffice.

This derivation only shows that at most 23 people are needed to ensure a birthday match with even chance; it leaves open the possibility that, say, n = 22 could also work.

[edit] Generalizations

[edit] Cast as a collision problem

The birthday problem can be generalized as follows: given n random integers drawn from a discrete uniform distribution with range [1,d], what is the probability p(n;d) that at least two numbers are the same?

The generic results can be derived using the same arguments given above.

$p(n;d) = \begin{cases} 1-\prod_{k=1}^{n-1}\left(1-{k \over d}\right) & n\le d \\ 1 & n > d \end{cases}$

$p(n;d) \approx 1 - e^{-(n(n-1))/2d}$

$q(n;d) = 1 - \left( \frac{d-1}{d} \right)^n$

$n(p;d)\approx \sqrt{2d\ln\left({1 \over 1-p}\right)}$

The birthday problem in this more generic sense applies to hash functions: the expected number of N-bit hashes that can be generated before getting a collision is not 2^N, but rather only 2^N/2. This is exploited by birthday attacks on cryptographic hash functions and is the reason why a small number of collisions in a hash table are, for all practical purposes, inevitable.

The theory behind the birthday problem was used by Zoe Schnabel^[6] under the name of capture-recapture statistics to estimate the size of fish population in lakes.

[edit] Generalization to multiple types

The basic problem considers all trials to be of one "type". The birthday problem has been generalized to consider an arbitrary number of types.^[7] In the simplest extension there are just two types, say m "men" and n "women", and the problem becomes characterizing the probability of a shared birthday between at least one man and one woman. (Shared birthdays between, say, two women do not count.) The probability of no (i.e. zero) shared birthdays here is

$p_0 = \frac{1}{d^{m+n}} \sum_{i=1}^m \sum_{j=1}^n S_2(m,i) S_2(n,j) \prod_{k=0}^{i+j-1} d - k$

where we set d = 365 and where S₂ are Stirling numbers of the second kind. Consequently, the desired probability is 1 − p₀.

This variation of the birthday problem is interesting because there is not a unique solution for the total number of people m + n. For example, the usual 0.5 probability value is realized for both a 32-member group of 16 men and 16 women and a 49-member group of 43 women and 6 men.

[edit] Other birthday problems

[edit] Reverse problem

For a fixed probability p:

Find the greatest n for which the probability p(n) is smaller than the given p, or
Find the smallest n for which the probability p(n) is greater than the given p.

An approximation to this can be derived by inverting the 'coarser' approximation above:

$n(p)\approx \sqrt{2\times 365\ln\left({1 \over 1-p}\right)}.$

[edit] Sample calculations

p	n	n↓	p(n↓)	n↑	p(n↑)
0.01	0.14178√365 = 2.70864	2	0.00274	3	0.00820
0.05	0.32029√365 = 6.11916	6	0.04046	7	0.05624
0.1	0.45904√365 = 8.77002	8	0.07434	9	0.09462
0.2	0.66805√365 = 12.76302	12	0.16702	13	0.19441
0.3	0.84460√365 = 16.13607	16	0.28360	17	0.31501
0.5	1.17741√365 = 22.49439	22	0.47570	23	0.50730
0.7	1.55176√365 = 29.64625	29	0.68097	30	0.70632
0.8	1.79412√365 = 34.27666	34	0.79532	35	0.81438
0.9	2.14597√365 = 40.99862	40	0.89123	41	0.90315
0.95	2.44775√365 = 46.76414	46	0.94825	47	0.95477
0.99	3.03485√365 = 57.98081	57	0.99012	58	0.99166

Note: some values falling outside the bounds have been colored to show that the approximation is not always exact.

[edit] First match

A related question is, as people enter a room one at a time, which one is most likely to be the first to have the same birthday as someone already in the room? That is, for what n is p(n) − p(n − 1) maximum? The answer is 20—if there's a prize for first match, the best position in line is 20th.

[edit] Same birthday as you

Comparing p(n) = probability of a birthday match with q(n) = probability of matching your birthday

Note that in the birthday problem, neither of the two people is chosen in advance. By way of contrast, the probability q(n) that someone in a room of n other people has the same birthday as a particular person (for example, you), is given by

$q(n) = 1 - \left( \frac{365-1}{365} \right)^n.$

Substituting n = 23 gives about 6.1%, which is less than 1 chance in 16. For a greater than 50% chance that one person in a roomful of n people has the same birthday as you, n would need to be at least 253. Note that this number is significantly higher than 365/2 = 182.5: the reason is that it is likely that there are some birthday matches among the other people in the room.

It is not a coincidence that $253=\frac{23\times(23-1)}{2}$ ; a similar approximate pattern can be found using a number of possibilities different from 365, or a target probability different from 50%.

[edit] Near matches

Another generalization is to ask how many people are needed in order to have a better than 50% chance that two people have a birthday within one day of each other, or within two, three, etc., days of each other. This is a more difficult problem and requires use of the inclusion-exclusion principle. The number of people required so that the probability that some pair will have a birthday separated by fewer than k days will be higher than 50% is:

k	# people required
1	23
2	14
3	11
4	9
5	8
6	8
7	7
8	7

Thus in a group of just seven random people, it is more likely than not that two of them will have a birthday within a week of each other.^[8]

[edit] Collision counting

The probability that the kth integer randomly chosen from [1, d] will repeat at least one previous choice equals q(k − 1; d) above. The expected total number of times a selection will repeat a previous selection as n such integers are chosen equals

$\sum_{k=1}^n q(k-1;d) = n - d + d \left (\frac {d-1} {d} \right )^n.$

[edit] Average number of people

In an alternative formulation of the birthday problem, one asks the average number of people required to find a pair with the same birthday. The problem is relevant to several hashing algorithms analyzed by Donald Knuth in his book The Art of Computer Programming. It may be shown^[9]^[10] that if one samples uniformly, with replacement, from a population of size M, the number of trials required for the first repeated sampling of some individual has expected value $\scriptstyle\overline{n}\,=\,1+Q(M)$ , where

$Q(M)=\sum_{k=1}^{M} \frac{M!}{(M-k)! M^k}.$

The function

$Q(M)= 1 + \frac{M-1}{M} + \frac{(M-1)(M-2)}{M^2} + \cdots + \frac{(M-1)(M-2) \cdots 1}{M^{M-1}}$

has been studied by Srinivasa Ramanujan and has asymptotic expansion:

$Q(M)\sim\sqrt{\frac{\pi M}{2}}-\frac{1}{3}+\frac{1}{12}\sqrt{\frac{\pi}{2n}}-\frac{4}{135n}+\cdots.$

With M = 365 days in a year, the average number of people required to find a pair with the same birthday is $\scriptstyle\overline{n}\,=\,1+Q(M)\approx 24.61658$ , slightly more than the number required for a 50% chance. In the best case, two people will suffice; at worst, the maximum possible number of M + 1 = 366 people is needed; but on average, only 25 people are required.

An informal demonstration of the problem can be made from the List of Prime Ministers of Australia, in which Paul Keating, the 24th Prime Minister, is the first to share a birthday with another on the list.

James K. Polk, the eleventh President of the United States of America, and Warren G. Harding, the twenty-ninth President, were both born on 2nd November, although in different years (1795 and 1865 respectively).

Of the 73 actors to win the Academy Award for Best Actor, there are six pairs of actors who share the same birthday.

Of the 67 actresses to win the Academy Award for Best Actress, there are three pairs of actresses who share the same birthday.

Of the 61 directors to win the Academy Award for Best Director, there are five pairs of directors who share the same birthday.

Of the 52 people to serve as Prime Minister of the United Kingdom, there are two pairs of men who share the same birthday.

[edit] Partition problem

A related problem is the partition problem, a variant of the knapsack problem from operations research. Some weights are put on a balance; each weight is an integer number of grams randomly chosen between one gram and one million grams (one metric ton). The question is whether one can usually (that is, with probability close to 1) transfer the weights between the left and right arms to balance the scale. (In case the sum of all the weights is an odd number of grams, a discrepancy of one gram is allowed.) If there are only two or three weights, the answer is very clearly no; although there are some combinations which work, the majority of randomly selected combinations of three weights do not. If there are very many weights, the answer is clearly yes. The question is, how many are just sufficient? That is, what is the number of weights such that it is equally likely for it to be possible to balance them as impossible?

Some people's intuition is that the answer is above 100,000. Most people's intuition is that it is in the thousands or tens of thousands, while others feel it should at least be in the hundreds. The correct answer is approximately 23.

The reason is that the correct comparison is to the number of partitions of the weights into left and right. There are 2^N−1 different partitions for N weights, and the left sum minus the right sum can be thought of as a new random quantity for each partition. The distribution of the sum of weights is approximately Gaussian, with a peak at 1,000,000 N and width $\scriptstyle 1,000,000\sqrt{N}$ , so that when 2^N−1 is approximately equal to $\scriptstyle 1,000,000\sqrt{N}$ the transition occurs. 2²³⁻¹ is about 4 million, while the width of the distribution is only 5 million.^[11]

[edit] Notes

^ This is not a paradox in the sense of leading to a logical contradiction, but is called a paradox because the mathematical truth contradicts naïve intuition: most people estimate that the chance is much lower than 50%.
^ In reality, birthdays are not evenly distributed throughout the year; there are more births per day in some seasons than in others, but for the purposes of this problem the distribution is treated as uniform.
^ In particular, many children are born in the summer, especially the months of August and September (for the northern hemisphere) [1], and in the U.S. it has been noted that many children are conceived around the holidays of Christmas and New Year's Day; and, in environments like classrooms where many people share a birth year, it becomes relevant that due to the way hospitals work, where C-sections and induced labor are not generally scheduled on the weekend, more children are born on Mondays and Tuesdays than on weekends. Both of these factors tend to increase the chance of identical birth dates, since a denser subset has more possible pairs (in the extreme case when everyone was born on three days, there would obviously be many identical birthdays). The birthday problem for such non-constant birthday probabilities was tackled by Murray Klamkin in 1967. A formal proof that the probability of two matching birthdays is least for a uniform distribution of birthdays was given by D. Bloom (1973)
^ Mathis, Frank H. (June 1991). "A Generalized Birthday Problem". SIAM Review (Society for Industrial and Applied Mathematics) 33 (2): 265–270. doi:10.1137/1033051. ISSN 00361445. OCLC 37699182. http://www.jstor.org/stable/2031144. Retrieved on 2008-07-08.
^ In his autobiography, Halmos criticized the form in which the birthday paradox is often presented, in terms of numerical computation. He believed that it should be used as an example in the use of more abstract mathematical concepts. He wrote:

The reasoning is based on important tools that all students of mathematics should have ready access to. The birthday problem used to be a splendid illustration of the advantages of pure thought over mechanical manipulation; the inequalities can be obtained in a minute or two, whereas the multiplications would take much longer, and be much more subject to error, whether the instrument is a pencil or an old-fashioned desk computer. What calculators do not yield is understanding, or mathematical facility, or a solid basis for more advanced, generalized theories.
^ Z. E. Schnabel (1938) The Estimation of the Total Fish Population of a Lake, American Mathematical Monthly 45, 348–352.
^ M. C. Wendl (2003) Collision Probability Between Sets of Random Variables, Statistics and Probability Letters 64(3), 249–254.
^ M. Abramson and W. O. J. Moser (1970) More Birthday Surprises, American Mathematical Monthly 77, 856–858
^ D. E. Knuth; The Art of Computer Programming. Vol. 3, Sorting and Searching (Addison-Wesley, Reading, Massachusetts, 1973)
^ P. Flajolet, P. J. Grabner, P. Kirschenhofer, H. Prodinger (1995), On Ramanujan's Q-Function, Journal of Computational and Applied Mathematics 58, 103–116
^ C. Borgs, J. Chayes, and B. Pittel (2001) Phase Transition and Finite Size Scaling in the Integer Partition Problem, Random Structures and Algorithms 19(3–4), 247–288.

[edit] References

E. H. McKinney (1966) Generalized Birthday Problem, American Mathematical Monthly 73, 385–387.
M. Klamkin and D. Newman (1967) Extensions of the Birthday Surprise, Journal of Combinatorial Theory 3, 279–282.
M. Abramson and W. O. J. Moser (1970) More Birthday Surprises, American Mathematical Monthly 77, 856–858
D. Bloom (1973) A Birthday Problem, American Mathematical Monthly 80, 1141–1142.
Shirky, Clay Here Comes Everybody: The Power of Organizing Without Organizations, (2008.) New York. 25–27.

[edit] External links

[0] This is not a paradox in the sense of leading to a logical contradiction, but is called a paradox because the mathematical truth contradicts naïve intuition: most people estimate that the chance is much lower than 50%.

[1] In reality, birthdays are not evenly distributed throughout the year; there are more births per day in some seasons than in others, but for the purposes of this problem the distribution is treated as uniform.

[2] In particular, many children are born in the summer, especially the months of August and September (for the northern hemisphere) [1], and in the U.S. it has been noted that many children are conceived around the holidays of Christmas and New Year's Day; and, in environments like classrooms where many people share a birth year, it becomes relevant that due to the way hospitals work, where C-sections and induced labor are not generally scheduled on the weekend, more children are born on Mondays and Tuesdays than on weekends. Both of these factors tend to increase the chance of identical birth dates, since a denser subset has more possible pairs (in the extreme case when everyone was born on three days, there would obviously be many identical birthdays). The birthday problem for such non-constant birthday probabilities was tackled by Murray Klamkin in 1967. A formal proof that the probability of two matching birthdays is least for a uniform distribution of birthdays was given by D. Bloom (1973)

[3] Mathis, Frank H. (June 1991). "A Generalized Birthday Problem". SIAM Review (Society for Industrial and Applied Mathematics) 33 (2): 265–270. doi:10.1137/1033051. ISSN 00361445. OCLC 37699182. http://www.jstor.org/stable/2031144. Retrieved on 2008-07-08.

[4] In his autobiography, Halmos criticized the form in which the birthday paradox is often presented, in terms of numerical computation. He believed that it should be used as an example in the use of more abstract mathematical concepts. He wrote:

The reasoning is based on important tools that all students of mathematics should have ready access to. The birthday problem used to be a splendid illustration of the advantages of pure thought over mechanical manipulation; the inequalities can be obtained in a minute or two, whereas the multiplications would take much longer, and be much more subject to error, whether the instrument is a pencil or an old-fashioned desk computer. What calculators do not yield is understanding, or mathematical facility, or a solid basis for more advanced, generalized theories.

[5] Z. E. Schnabel (1938) The Estimation of the Total Fish Population of a Lake, American Mathematical Monthly 45, 348–352.

[6] M. C. Wendl (2003) Collision Probability Between Sets of Random Variables, Statistics and Probability Letters 64(3), 249–254.

[abramson-7] M. Abramson and W. O. J. Moser (1970) More Birthday Surprises, American Mathematical Monthly 77, 856–858

[knuth73-8] D. E. Knuth; The Art of Computer Programming. Vol. 3, Sorting and Searching (Addison-Wesley, Reading, Massachusetts, 1973)

[flajolet95-9] P. Flajolet, P. J. Grabner, P. Kirschenhofer, H. Prodinger (1995), On Ramanujan's Q-Function, Journal of Computational and Applied Mathematics 58, 103–116

[10] C. Borgs, J. Chayes, and B. Pittel (2001) Phase Transition and Finite Size Scaling in the Integer Partition Problem, Random Structures and Algorithms 19(3–4), 247–288.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]