Langton's ant
From Wikipedia, the free encyclopedia
Langton's ant is a two-dimensional Turing machine with a very simple set of rules but complicated emergent behavior. It was invented by Chris Langton in 1986.
Contents |
[edit] Rules
Squares on a plane are colored variously either black or white. We arbitrarily identify one square as the "ant". The ant can travel in any of the four cardinal directions at each step it takes. The ant moves according to the rules below:
- At a black square, turn 90° right, flip the color of the square, move forward one unit
- At a white square, turn 90° left, flip the color of the square, move forward one unit
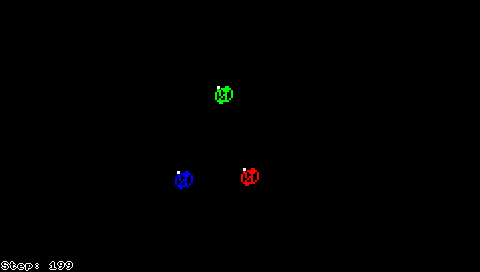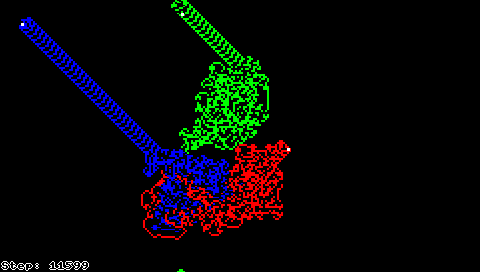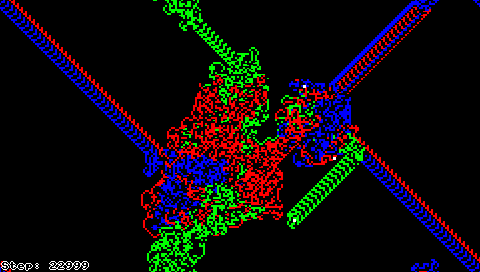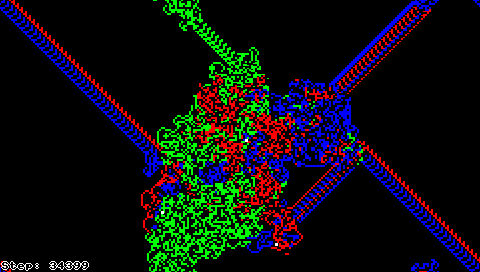
These simple rules lead to surprisingly complex behavior: after an initial period of apparently chaotic behavior, the ant starts building a recurrent pattern of 104 steps that repeat indefinitely when all squares in the grid have initially the same color. Other initial configurations seem eventually to converge to similar repetitive patterns suggesting that the "highway" is an attractor of Langton's ant, but no one has been able to prove that this is true for all initial configurations. It is only known that ant's trajectory is always unbounded regardless of the initial configuration.[1]
Langton's ant can also be described as a cellular automaton, where most of the grid is colored black or white, and the "ant" square has one of eight different colors assigned to encode the combination of black/white state and the current direction of motion of the ant.
[edit] Extension to Langton's ant
There is a simple extension to Langton's ant where instead of just two colors, more colors are used. The colors are modified in a cyclic fashion. There is also a simple name giving scheme for such ants: for each of the successive colours, a letter 'L' or 'R' is used to indicate whether a left or right turn should be taken. Langton's ant would get the name 'RL' in this name giving scheme.
Some of these extended Langton's ants produce patterns that become symmetric over and over again. One of the simplest examples is the ant 'RLLR'. One sufficient condition for this to happen is that the ant's name, seen as a cyclic list, consists of consecutive pairs of identical letters 'LL' or 'RR' (the term "cyclic list" indicates that the last letter may pair with the first one.)
[edit] Universality of Langton's Ant
By the year 2000, Gajardo et al. showed a construction that calculates any boolean circuit using the trajectory of a single instance of Langton's ant.[2] Thus, it would be possible to simulate a Turing machine using the ant's trajectory for computation. This means that the ant is capable of universal computation.
[edit] References
- ^ Bunimovich, Leonid A.; Serge E. Troubetzkoy (1992). "Recurrence properties of Lorentz lattice gas cellular automata". Journal of Statistical Physics 67: 289–302. doi:.
- ^ Gajardo, A.; A. Moreira, E. Goles (15 March 2002). "Complexity of Langton's ant". Discrete Applied Mathematics 117: 41–50. doi:.
[edit] External links
| Wikimedia Commons has media related to: Langton's ant |
- Further Travels with my Ant by D. Gale, J. Propp, S. Sutherland, and S. Troubetzkoy: an article in PostScript or TeX format that contains a proof of the above sufficient condition for symmetric patterns.
- Langton's Ant Software
- Generalized Ants
- Java applet with multiple colours and programmable ants
- ASM32 application with zooming, adding obstacles, save&load, inverting colours, step by step mode
- A Scientific American Mathematical Recreations column using Langton's Ant as a metaphor for a Theory of everything.
- Java applet on several grids and editable graphs, it shows how the ant can compute logical gates
- Langton's ants in Python.
- Another simulation of Langton's ant in Python.
- Paterson's worms
- Online demonstration of Langton's ant