Standard error (statistics)
From Wikipedia, the free encyclopedia
The standard error of a method of measurement or estimation is the standard deviation of the sampling distribution associated with the estimation method.[1] The term may also be used to refer to an estimate of that standard deviation, derived from a particular sample used to compute the estimate.
For example, the sample mean is the usual estimator of a population mean. However, different samples drawn from that same population would in general have different values of the sample mean. The standard error of the mean (i.e., of using the sample mean as a method of estimating the population mean) is the standard deviation of those sample means over all possible samples (of a given size) drawn from the population. Secondarily, the standard error of the mean can refer to an estimate of that standard deviation, computed from the sample of data being analysed at the time.
The term standard error is derived from the fact that, as long as the estimator is unbiased, the standard deviation of the error (the difference between the estimate and the true value) is the same as the standard deviation of the estimates themselves; this is true since the standard deviation of the difference between the random variable and its expected value is equal to the standard deviation of a random variable itself.
In many practical applications, the true value of the standard deviation is usually unknown. As a result, the term standard error is often used to refer to an estimate of this unknown quantity. In such cases it is important to be clear about what has been done and to attempt to take proper account of the fact that the standard error is only an estimate. Unfortunately, this is not often possible and it may then be better to use an approach that avoids using a standard error, for example by using maximum likelihood or a more formal approach to deriving confidence intervals. One well-known case where a proper allowance can be made arises where the Student's t-distribution is used to provide a confidence interval for an estimated mean or difference of means. In other cases, the standard error may usefully be used to provide an indication of the size of the uncertainty, but its formal or semi-formal use to provide confidence intervals or tests should be avoided unless the sample size is at least moderately large. Here "large enough" would depend on the particular quantities being analysed.
Contents |
[edit] Standard error of the mean
The standard error of the mean (SEM) is the standard deviation of the sample mean estimate of a population mean. (It can also be viewed as the standard deviation of the error in the sample mean relative to the true mean, since the sample mean is an unbiased estimator.) SEM is usually estimated by the sample estimate of the population standard deviation (sample standard deviation) divided by the square root of the sample size (assuming statistical independence of the values in the sample):
where
- s is the sample standard deviation (i.e. the sample based estimate of the standard deviation of the population), and
- n is the size (number of observations) of the sample.
This estimate may be compared with the formula for the true standard deviation of the mean:
where
- σ is the standard deviation of the population.
Note 1: Standard error may also be defined as the standard deviation of the residual error term. (Kenney and Keeping, p. 187; Zwillinger 1995, p. 626)
Note 2: Both the standard error and the standard deviation of small samples tend to systematically underestimate the population standard error and deviations: the standard error of the mean is a biased estimator of the population standard error. With n = 2 the underestimate is about 25%, but for n = 6 the underestimate is only 5%. Gurland and Tripathi (1971) provide a correction and equation for this effect (see Sokal and Rohlf, Biometry, 2nd ed., 1981, p 53 for an equation of the correction factor for small samples of n < 20.
A practical result: Decreasing the uncertainty in your mean value estimate by a factor of two requires that you acquire four times as many observations in your sample. Worse, decreasing standard error by a factor of ten requires a hundred times as many observations.
[edit] Assumptions and usage
If the data are assumed to be normally distributed, quantiles of the normal distribution and the sample mean and standard error can be used to calculate approximate confidence intervals for the mean. The following expressions can be used to calculate the upper and lower 95% confidence limits, where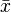 
is equal to the sample mean, SE is equal to the standard error for the sample mean, and 1.96 is the .975 quantile of the normal distribution:
- Upper 95% Limit =
- Lower 95% Limit =
In particular, the standard error of a sample statistic (such as sample mean) is the estimated standard deviation of the error in the process by which it was generated. In other words, it is the standard deviation of the sampling distribution of the sample statistic. The notation for standard error can be any one of SE, SEM (for standard error of measurement or mean), or SE.
Standard errors provide simple measures of uncertainty in a value and are often used because:
- If the standard error of several individual quantities is known then the standard error of some function of the quantities can be easily calculated in many cases;
- Where the probability distribution of the value is known, it can be used to calculate a good approximation to an exact confidence interval; and
- Where the probability distribution is unknown, relationships like Chebyshev’s or the Vysochanskiï-Petunin inequality can be used to calculate a conservative confidence interval
- As the sample size tends to infinity the central limit theorem guarantees that the sampling distribution of the mean is asymptotically normal.
[edit] Correction for correlation in the sample
If values of the measured quantity A are not statistically independent but have been obtained from known locations in parameter space x, an unbiased estimate of error in the mean may be obtained by multiplying the standard error above by the factor f:
where the sample bias coefficient ρ is the average of the autocorrelation-coefficient ρAA[Δx] value (a quantity between -1 and 1) for all sample point pairs.
[edit] See also
[edit] References
- ^ Everitt, B.S. (2003) The Cambridge Dictionary of Statistics, CUP. ISBN 0-521-81099-x
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
