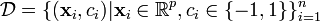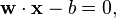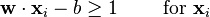Support vector machine
From Wikipedia, the free encyclopedia
|
This article or section has multiple issues. Please help improve the article or discuss these issues on the talk page.
|
Support vector machines (SVMs) are a set of related supervised learning methods used for classification and regression. Viewing input data as two sets of vectors in an n-dimensional space, an SVM will construct a separating hyperplane in that space, one which maximizes the margin between the two data sets. To calculate the margin, two parallel hyperplanes are constructed, one on each side of the separating hyperplane, which are "pushed up against" the two data sets. Intuitively, a good separation is achieved by the hyperplane that has the largest distance to the neighboring datapoints of both classes, since in general the larger the margin the lower the generalization error of the classifier.
Contents |
[edit] Motivation
Classifying data is a common need in machine learning. Suppose some given data points each belong to one of two classes, and the goal is to decide which class a new data point will be in. In the case of support vector machines, a data point is viewed as a p-dimensional vector (a list of p numbers), and we want to know whether we can separate such points with a p − 1-dimensional hyperplane. This is called a linear classifier. There are many hyperplanes that might classify the data. However, we are additionally interested in finding out if we can achieve maximum separation (margin) between the two classes. By this we mean that we pick the hyperplane so that the distance from the hyperplane to the nearest data point is maximized. That is to say that the nearest distance between a point in one separated hyperplane and a point in the other separated hyperplane is maximized. Now, if such a hyperplane exists, it is clearly of interest and is known as the maximum-margin hyperplane and such a linear classifier is known as a maximum margin classifier.
[edit] Formalization
We are given some training data, a set of points of the form
where the ci is either 1 or −1, indicating the class to which the point  belongs. Each
belongs. Each  is a p-dimensional real vector. We want to give the maximum-margin hyperplane which divides the points having ci = 1 from those having ci = − 1. Any hyperplane can be written as the set of points
is a p-dimensional real vector. We want to give the maximum-margin hyperplane which divides the points having ci = 1 from those having ci = − 1. Any hyperplane can be written as the set of points  satisfying
satisfying
where  denotes the dot product. The vector
denotes the dot product. The vector  is a normal vector: it is perpendicular to the hyperplane. The parameter
is a normal vector: it is perpendicular to the hyperplane. The parameter  determines the offset of the hyperplane from the origin along the normal vector
determines the offset of the hyperplane from the origin along the normal vector  .
.
We want to choose the  and b to maximize the margin, or distance between the parallel hyperplanes that are as far apart as possible while still separating the data. These hyperplanes can be described by the equations
and b to maximize the margin, or distance between the parallel hyperplanes that are as far apart as possible while still separating the data. These hyperplanes can be described by the equations
and
Note that if the training data are linearly separable, we can select the two hyperplanes of the margin in a way that there are no points between them and then try to maximize their distance. By using geometry, we find the distance between these two hyperplanes is 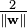 , so we want to minimize
, so we want to minimize 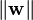 . As we also have to prevent data points falling into the margin, we add the following constraint: for each i either
. As we also have to prevent data points falling into the margin, we add the following constraint: for each i either
of the first class or
 of the second.
of the second.
This can be rewritten as:
We can put this together to get the optimization problem:
Minimize (in  )
)
subject to (for any  )
)
[edit] Primal form
The optimization problem presented in the preceding section is difficult to solve because it depends on ||w||, the norm of w, which involves a square root. Fortunately it is possible to alter the equation by substituting ||w|| with  without changing the solution (the minimum of the original and the modified equation have the same w and b). This is a quadratic programming (QP) optimization problem. More clearly:
without changing the solution (the minimum of the original and the modified equation have the same w and b). This is a quadratic programming (QP) optimization problem. More clearly:
Minimize (in  )
)
subject to (for any  )
)
The factor of 1/2 is used for mathematical convenience. This problem can now be solved by standard quadratic programming techniques and programs.
[edit] Dual form
Writing the classification rule in its unconstrained dual form reveals that the maximum margin hyperplane and therefore the classification task is only a function of the support vectors, the training data that lie on the margin. The dual of the SVM can be shown to be the following optimization problem:
Maximize (in αi )
subject to (for any  )
)
and
The α terms constitute a dual representation for the weight vector in terms of the training set:
[edit] Biased and unbiased hyperplanes
For simplicity reasons, sometimes it is required that the hyperplane passes through the origin of the coordinate system. Such hyperplanes are called unbiased, whereas general hyperplanes not necessarily passing through the origin are called biased. An unbiased hyperplane can be enforced by setting b = 0 in the primal optimization problem. The corresponding dual is identical to the dual given above without the equality constraint
[edit] Transductive support vector machines
Transductive support vector machines extend SVMs in that they also take into account structural properties (e.g. correlational structures) of the data set to be classified. Here, in addition to the training set  , the learner is also given a set
, the learner is also given a set
of test examples to be classified. Formally, a transductive support vector machine is defined by the following primal optimization problem:
Minimize (in  )
)
subject to (for any  and any
and any  )
)
and
Transductive support vector machines have been introduced by Vladimir Vapnik in 1998.
[edit] Properties
SVMs belong to a family of generalized linear classifiers. They can also be considered a special case of Tikhonov regularization. A special property is that they simultaneously minimize the empirical classification error and maximize the geometric margin; hence they are also known as maximum margin classifiers.
A comparison of the SVM to other classifiers has been made by Meyer, Leisch and Hornik.[1]
[edit] Extensions to the linear SVM
[edit] Soft margin
In 1995, Corinna Cortes and Vladimir Vapnik suggested a modified maximum margin idea that allows for mislabeled examples.[2] If there exists no hyperplane that can split the "yes" and "no" examples, the Soft Margin method will choose a hyperplane that splits the examples as cleanly as possible, while still maximizing the distance to the nearest cleanly split examples. The method introduces slack variables, ξi, which measure the degree of misclassification of the datum xi
The objective function is then increased by a function which penalizes non-zero ξi, and the optimization becomes a trade off between a large margin, and a small error penalty. If the penalty function is linear, the equation (3) now transforms to
This constraint in (2) along with the objective of minimizing 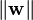 can be solved using Lagrange multipliers. The key advantage of a linear penalty function is that the slack variables vanish from the dual problem, with the constant C appearing only as an additional constraint on the Lagrange multipliers. Non-linear penalty functions have been used, particularly to reduce the effect of outliers on the classifier, but unless care is taken, the problem becomes non-convex, and thus it is considerably more difficult to find a global solution.
can be solved using Lagrange multipliers. The key advantage of a linear penalty function is that the slack variables vanish from the dual problem, with the constant C appearing only as an additional constraint on the Lagrange multipliers. Non-linear penalty functions have been used, particularly to reduce the effect of outliers on the classifier, but unless care is taken, the problem becomes non-convex, and thus it is considerably more difficult to find a global solution.
[edit] Non-linear classification
The original optimal hyperplane algorithm proposed by Vladimir Vapnik in 1963 was a linear classifier. However, in 1992, Bernhard Boser, Isabelle Guyon and Vapnik suggested a way to create non-linear classifiers by applying the kernel trick (originally proposed by Aizerman et al..[3] ) to maximum-margin hyperplanes.[4] The resulting algorithm is formally similar, except that every dot product is replaced by a non-linear kernel function. This allows the algorithm to fit the maximum-margin hyperplane in the transformed feature space. The transformation may be non-linear and the transformed space high dimensional; thus though the classifier is a hyperplane in the high-dimensional feature space it may be non-linear in the original input space.
If the kernel used is a Gaussian radial basis function, the corresponding feature space is a Hilbert space of infinite dimension. Maximum margin classifiers are well regularized, so the infinite dimension does not spoil the results. Some common kernels include,
- Polynomial (homogeneous):
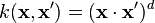
- Polynomial (inhomogeneous):

- Radial Basis Function:
 , for γ > 0
, for γ > 0 - Gaussian Radial basis function:

- Hyperbolic tangent:
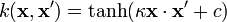 , for some (not every) κ > 0 and c < 0
, for some (not every) κ > 0 and c < 0
[edit] Multiclass SVM
Multiclass SVM aims to assign labels to instances by using support vector machines, where the labels are drawn from a finite set of several elements. The dominating approach for doing so is to reduce the single multiclass problem into multiple binary problems. Each of the problems yields a binary classifier, which is assumed to produce an output function that gives relatively large values for examples from the positive class and relatively small values for examples belonging to the negative class. Two common methods to build such binary classifiers are where each classifier distinguishes between (i) one of the labels to the rest (one-versus-all) or (ii) between every pair of classes (one-versus-one). Classification of new instances for one-versus-all case is done by a winner-takes-all strategy, in which the classifier with the highest output function assigns the class. The classification of one-versus-one case is done by a max-wins voting strategy, in which every classifier assigns the instance to one of the two classes, then the vote for the assigned class is increased by one vote, and finally the class with most votes determines the instance classification.
[edit] Structured SVM
Support vector machines have been generalized to Structured SVM, where the label space is structured and of possibly infinite size.
[edit] Regression
A version of a SVM for regression was proposed in 1996 by Vladimir Vapnik, Harris Drucker, Chris Burges, Linda Kaufman and Alex Smola.[5] This method is called support vector regression (SVR). The model produced by support vector classification (as described above) only depends on a subset of the training data, because the cost function for building the model does not care about training points that lie beyond the margin. Analogously, the model produced by SVR only depends on a subset of the training data, because the cost function for building the model ignores any training data that are close (within a threshold ε) to the model prediction.
[edit] Implementation
The parameters of the maximum-margin hyperplane are derived by solving the optimization. There exist several specialized algorithms for quickly solving the QP problem that arises from SVMs, mostly reliant on heuristics for breaking the problem down into smaller, more-manageable chunks. A common method for solving the QP problem is the Platt's Sequential Minimal Optimization (SMO) algorithm, which breaks the problem down into 2-dimensional sub-problems that may be solved analytically, eliminating the need for a numerical optimization algorithm such as conjugate gradient methods.
Another approach is to use an interior point method that uses Newton-like iterations to find a solution of the Karush-Kuhn-Tucker conditions of the primal and dual problems.[6] Instead of solving a sequence of broken down problems, this approach directly solves the problem as a whole. To avoid solving a linear system involving the large kernel matrix, a row rank approximation to the matrix is often used to use the kernel trick.
[edit] See also
- Kernel machines
- Predictive analytics
- Relevance vector machine, a probabilistic sparse kernel model identical in functional form to SVM.
[edit] External links
[edit] General
- A tutorial on SVMs has been produced by C.J.C Burges.[7]
- www.kernel-machines.org (general information and collection of research papers)
- www.support-vector-machines.org (Literature, Review, Software, Links related to Support Vector Machines — Academic Site)
- videolectures.net (SVM-related video lectures)
- Animation clip: SVM with polynomial kernel visualization.
- A very basic SVM tutorial for complete beginners by Tristan Fletcher [1].
[edit] Software
- ADAPA — a batch and real-time PMML based scoring engine for data mining models including Support Vector Machines.
- Algorithm::SVM — Perl bindings for the libsvm Support Vector Machine library
- dlib C++ Library — A C++ library that includes an easy to use SVM classifier
- e1071 — Machine learning library for R
- Gist — implementation of the SVM algorithm with feature selection.
- kernlab — Kernel-based Machine Learning library for R
- LIBLINEAR — A Library for Large Linear Classification, Machine Learning Group at National Taiwan University
- LIBSVM — A Library for Support Vector Machines, Chih-Chung Chang and Chih-Jen Lin
- Lush — a Lisp-like interpreted/compiled language with C/C++/Fortran interfaces that has packages to interface to a number of different SVM implementations. Interfaces to LASVM, LIBSVM, mySVM, SVQP, SVQP2 (SVQP3 in future) are available. Leverage these against Lush's other interfaces to machine learning, hidden markov models, numerical libraries (LAPACK, BLAS, GSL), and builtin vector/matrix/tensor engine.
- LS-SVMLab — Matlab/C SVM toolbox — well-documented, many features
- mlpy — Machine Learning Py — Python/NumPy based package for machine learning.
- NSvm Open source SVM implementation for .NET in C#.
- OSU SVM — Matlab implementation based on LIBSVM
- pcSVM is an object oriented SVM framework written in C++ and provides wrapping to Python classes. The site provides a stand alone demo tool for experimenting with SVMs.
- PCP — C program for supervised pattern classification. Includes LIBSVM wrapper.
- PyML — a Python machine learning package. Includes: SVM, nearest neighbor classifiers, ridge regression, Multi-class methods (one-against-one and one-against-rest), Feature selection (filter methods, RFE, multiplicative update, Model selection, Classifier testing (cross-validation, error rates, ROC curves, statistical test for comparing classifiers).
- Shogun — Large Scale Machine Learning Toolbox that provides several SVM implementations (like libSVM, SVMlight) under a common framework and interfaces to Octave, Matlab, Python, R
- SimpleSVM — SimpleSVM toolbox for Matlab
- SVM-KM — SVM and Kernel Methodes toolbox for Matlab
- SimpleMKL - Multiple Kernel Learning toolbox for Matlab
- Spider — Machine learning library for Matlab
- Statistical Pattern Recognition Toolbox for Matlab.
- SVM and Kernel Methods Matlab Toolbox
- SVM Classification Applet — Performs classification on any given data set and gives 10-fold cross-validation error rate
- SVMlight — a popular implementation of the SVM algorithm by Thorsten Joachims; it can be used to solve classification, regression and ranking problems.
- automation of SVMlight in Matlab — complete automation of SVMlight for use with fMRI data
- SVMProt — Protein Functional Family Prediction.
- Torch — C++ machine learning library with SVM
- The Kernel-Machine Library (GNU) C++ template library for Support Vector Machines
- TinySVM — a small SVM implementation, written in C++
- YALE (now RapidMiner) — a powerful machine learning toolbox containing wrappers for SVMLight, LibSVM, and MySVM in addition to many evaluation and preprocessing methods.
- Weka — a machine learning toolkit that includes an implementation of an SVM classifier; Weka can be used both interactively though a graphical interface or as a software library. (The SVM implementation is called "SMO". It can be found in the Weka Explorer GUI, under the "functions" category or in the Weka Explorer GUI as SVMAttributeEval, under Select attributes, attributeSelection.)
[edit] Interactive SVM applications
- ECLAT classification of Expressed Sequence Tag (EST) from mixed EST pools using codon usage
- EST3 classification of Expressed Sequence Tag (EST) from mixed EST pools using nucleotide triples
[edit] References
- ^ David Meyer, Friedrich Leisch, and Kurt Hornik. The support vector machine under test. Neurocomputing 55(1-2): 169-186, 2003 http://dx.doi.org/10.1016/S0925-2312(03)00431-4
- ^ Corinna Cortes and V. Vapnik, "Support-Vector Networks", Machine Learning, 20, 1995. http://www.springerlink.com/content/k238jx04hm87j80g/
- ^ M. Aizerman, E. Braverman, and L. Rozonoer (1964). "Theoretical foundations of the potential function method in pattern recognition learning". Automation and Remote Control 25: 821–837.
- ^ B. E. Boser, I. M. Guyon, and V. N. Vapnik. A training algorithm for optimal margin classifiers. In D. Haussler, editor, 5th Annual ACM Workshop on COLT, pages 144-152, Pittsburgh, PA, 1992. ACM Press
- ^ Harris Drucker, Chris J.C. Burges, Linda Kaufman, Alex Smola and Vladimir Vapnik (1997). "Support Vector Regression Machines". Advances in Neural Information Processing Systems 9, NIPS 1996, 155-161, MIT Press.
- ^ M. Ferris, and T. Munson (2002). "Interior-point methods for massive support vector machines". SIAM Journal on Optimization 13: 783–804.
- ^ Christopher J. C. Burges. "A Tutorial on Support Vector Machines for Pattern Recognition". Data Mining and Knowledge Discovery 2:121–167, 1998 http://research.microsoft.com/~cburges/papers/SVMTutorial.pdf
[edit] Bibliography
- Nello Cristianini and John Shawe-Taylor. An Introduction to Support Vector Machines and other kernel-based learning methods. Cambridge University Press, 2000. ISBN 0-521-78019-5 ([2] SVM Book)
- Huang T.-M., Kecman V., Kopriva I. (2006), Kernel Based Algorithms for Mining Huge Data Sets, Supervised, Semi-supervised, and Unsupervised Learning, Springer-Verlag, Berlin, Heidelberg, 260 pp. 96 illus., Hardcover, ISBN 3-540-31681-7[3]
- Vojislav Kecman: "Learning and Soft Computing - Support Vector Machines, Neural Networks, Fuzzy Logic Systems", The MIT Press, Cambridge, MA, 2001.[4]
- Bernhard Schölkopf and A. J. Smola: Learning with Kernels. MIT Press, Cambridge, MA, 2002. (Partly available on line: [5].) ISBN 0-262-19475-9
- Bernhard Schölkopf, Christopher J.C. Burges, and Alexander J. Smola (editors). "Advances in Kernel Methods: Support Vector Learning". MIT Press, Cambridge, MA, 1999. ISBN 0-262-19416-3. [6]
- John Shawe-Taylor and Nello Cristianini. Kernel Methods for Pattern Analysis. Cambridge University Press, 2004. ISBN 0-521-81397-2 ([7] Kernel Methods Book)
- Ingo Steinwart and Andreas Christmann. Support Vector Machines. Springer-Verlag, New York, 2008. ISBN 978-0-387-77241-7 ([8] SVM Book)
- P.J. Tan and D.L. Dowe (2004), MML Inference of Oblique Decision Trees, Lecture Notes in Artificial Intelligence (LNAI) 3339, Springer-Verlag, pp1082-1088. (This paper uses minimum message length (MML) and actually incorporates probabilistic support vector machines in the leaves of decision trees.)
- Vladimir Vapnik. The Nature of Statistical Learning Theory. Springer-Verlag, 1995. ISBN 0-387-98780-0
- Vladimir Vapnik, S.Kotz "Estimation of Dependences Based on Empirical Data" Springer, 2006. ISBN 0387308652, 510 pages [this is a reprint of Vapnik's early book describing philosophy behind SVM approach. The 2006 Appendix describes recent development].
- Dmitriy Fradkin and Ilya Muchnik "Support Vector Machines for Classification" in J. Abello and G. Carmode (Eds) "Discrete Methods in Epidemiology", DIMACS Series in Discrete Mathematics and Theoretical Computer Science, volume 70, pp. 13–20, 2006. [9]. Succinctly describes theoretical ideas behind SVM.
- Kristin P. Bennett and Colin Campbell, "Support Vector Machines: Hype or Hallelujah?", SIGKDD Explorations, 2,2, 2000, 1-13. [10]. Excellent introduction to SVMs with helpful figures.
- Ovidiu Ivanciuc, "Applications of Support Vector Machines in Chemistry", In: Reviews in Computational Chemistry, Volume 23, 2007, pp. 291–400. Reprint available: [11]
- Catanzaro, Sundaram, Keutzer, "Fast Support Vector Machine Training and Classification on Graphics Processors", In: International Conference on Machine Learning, 20080 [12]