Magnet
From Wikipedia, the free encyclopedia

A magnet (from Greek μαγνήτης λίθος, "Magnesian stone") is a material or object that produces a magnetic field. This magnetic field is invisible but is responsible for the most notable property of a magnet: a force that pulls on other ferromagnetic materials and attracts or repels other magnets.
A permanent magnet is one made from a material that stays magnetized. An example is a magnet used to hold notes on a refrigerator door. Materials which can be magnetized, which are also the ones that are strongly attracted to a magnet, are called ferromagnetic. These include iron, nickel, cobalt, some rare earth metals and some of their alloys (e.g Alnico), and some naturally occurring minerals such as lodestone. Permanent magnets are made from "hard" ferromagnetic materials which are designed to stay magnetized, while "soft" ferromagnetic materials like soft iron are attracted to a magnet but do not tend to stay magnetized.
An electromagnet is made from a coil of wire which acts as a magnet when an electric current passes through it, but stops being a magnet when the current stops. Often an electromagnet is wrapped around a core of ferromagnetic material like steel, which enhances the magnetic field produced by the coil.
Although ferromagnetic materials are the only ones strongly enough attracted to a magnet to be commonly considered "magnetic", all other substances respond weakly to a magnetic field, by one of several other types of magnetism. Paramagnetic materials, such as aluminum and oxygen are weakly attracted to a magnet. Diamagnetic materials, such as carbon and water, which include all substances not having another type of magnetism, are weakly repelled by a magnet.
The overall strength of a magnet is measured by its magnetic moment, while the local strength of the magnetism in a material is measured by its magnetization.
[edit] Background on the physics of magnetism and magnets
[edit] Magnetic field
The magnetic field (usually denoted B) is called a field because it has a value at every point in space. The magnetic field (at a given point) is specified by two properties: (1) its direction, which is along the orientation of a compass needle; and (2) its magnitude (also called strength), which is proportional to how strongly the compass needle orients along that direction. Direction and magnitude makes B a vector, so B is a vector field. (B can also depend on time.) In SI units the strength of the magnetic field is given in tesla.
[edit] Magnetic moment
A magnet's magnetic moment (also called magnetic dipole moment, and usually denoted μ) is a vector that characterizes the magnet's overall magnetic properties. For a bar magnet, the direction of the magnetic moment points from the magnet's south pole to its north pole[1], and the magnitude relates to how strong and how far apart these poles are. In SI units the magnetic moment is specified in terms of A·m².
A magnet both produces its own magnetic field and it responds to magnetic fields. The strength of the magnetic field it produces is at any given point proportional to the magnitude of its magnetic moment. In addition, when the magnet is put into an "external" magnetic field produced by a different source, it is subject to a torque tending to orient the magnetic moment parallel to the field. The amount of this torque is proportional both to the magnetic moment and the "external" field. A magnet may also be subject to a force driving it in one direction or another, according to the positions and orientations of the magnet and source. If the field is uniform in space the magnet is subject to no net force, although it is subject to a torque.
A wire in the shape of a circle with area A and carrying current I is a magnet, with a magnetic moment of magnitude equal to IA.
[edit] Magnetization
The magnetization of a magnetized material is the local value of its magnetic moment per unit volume, usually denoted M, with units A/m. It is a vector field, rather than just a vector (like the magnetic moment), because different areas in a magnet can be magnetized with different directions and strengths (for example, because of domains, see below). A good bar magnet may have a magnetic moment of magnitude 0.1 A·m² and a volume of 1 cm³, or 0.000001 m³, and therefore an average magnetization magnitude is 100,000 A/m. Iron can have a magnetization of around a million A/m. Such a large value explains why magnets are so effective at producing magnetic fields.
[edit] Two models for magnets: magnetic poles and atomic currents
Magnetic pole model: Although for many purposes it is convenient to think of a magnet as having distinct north and south magnetic poles, the concept of poles should not be taken literally: it is merely a way of referring to the two different ends of a magnet. The magnet does not have distinct "north" or "south" particles on opposing sides. (No magnetic monopole has yet been observed.) If a bar magnet is broken in half, in an attempt to separate the north and south poles, the result will be two bar magnets, each of which has both a north and south pole.
The magnetic pole approach is used by professional magneticians to design permanent magnets. In this approach, the pole surfaces of a permanent magnet are imagined to be covered with 'magnetic charge', little 'north pole' particles on the north pole and 'south poles' on the south pole, that are the source of the magnetic field lines. If the magnetic pole distribution is known, then outside the magnet the pole model gives the magnetic field exactly. In the interior of the magnet this model fails to give the correct field, but (see Units and Calculations, below). This pole model is also called the "Gilbert model" of a magnetic dipole.[2] Griffiths suggests (p. 258): "My advice is to use the Gilbert model, if you like, to get an intuitive "feel" for a problem, but never rely on it for quantitative results."
Ampère model: Another model is the "Ampère model", where all magnetization is due to the effect of microscopic, or atomic, circular "bound currents", also called "Ampèrian currents" throughout the material. For a uniformly magnetized cylindrical bar magnet, the net effect of the microscopic bound currents is to make the magnet behave as if there is a macroscopic sheet of electric current flowing around the surface, with local flow direction normal to the cylinder axis. (Since scraping off the outer layer of a magnet will not destroy its magnetic field, it can be seen that this is just a model, and the tiny currents are actually distributed throughout the material). The right-hand rule tells which direction the current flows. The Ampere model gives the exact magnetic field both inside and outside the magnet. It is usually difficult to calculate the Amperian currents on the surface of a magnet, whereas it is often easier to find the effective poles for the same magnet.
[edit] Pole naming conventions
The north pole of the magnet is the pole which, when the magnet is freely suspended, points towards the Earth's magnetic north pole in northern Canada. Since opposite poles (north and south) attract whereas like poles (north and north, or south and south) repel, the Earth's present geographic north is thus actually its magnetic south. Confounding the situation further, the Earth's magnetic field has reversed itself many times in the distant past.
As a practical matter, in order to tell which pole of a magnet is north and which is south, it is not necessary to use the earth's magnetic field at all. For example, one calibration method would be to compare it to an electromagnet, whose poles can be identified by the right-hand rule.
[edit] Descriptions of magnetic behaviors
There are several types of magnetism, and all materials exhibit at least one of them. This section describes, qualitatively, the primary types of magnetic behavior that materials can show. The physics underlying each of these behaviors is described in the next section below, and can also be found in more detail in their respective articles.
- Ferromagnetic and ferrimagnetic materials are the ones normally thought of as 'magnetic'; they are attracted to a magnet strongly enough that the attraction can be felt. These materials are the only ones that can retain magnetization and become magnets; a common example is a traditional refrigerator magnet. Ferrimagnetic materials, which include ferrites and the oldest magnetic materials magnetite and lodestone, are similar to but weaker than ferromagnetics. The difference between ferro- and ferrimagnetic materials is related to their microscopic structure, as explained below.
- Paramagnetic substances such as platinum, aluminum, and oxygen are weakly attracted to a magnet. This effect is hundreds of thousands of times weaker than ferromagnetic materials attraction, so it can only be detected by using sensitive instruments, or using extremely strong magnets. Magnetic ferrofluids, although they are made of tiny ferromagnetic particles suspended in liquid, are sometimes considered paramagnetic since they cannot be magnetized.
- Diamagnetic means repelled by both poles. Compared to paramagnetic and ferromagnetic substances, diamagnetic substances such as carbon, copper, water, and plastic are even more weakly repelled by a magnet. The permeability of diamagnetic materials is less than the permeability of a vacuum. All substances not possessing one of the other types of magnetism are diamagnetic; this includes most substances. Although force on a diamagnetic object from an ordinary magnet is far too weak to be felt, using extremely strong superconducting magnets diamagnetic objects such as pieces of lead and even frogs can be levitated so they float in midair. Superconductors repel magnetic fields from their interior and are strongly diamagnetic.
[edit] Physics of magnetic behaviors
[edit] Overview
Magnetism, at its root, arises from two sources:
- Electric currents, or more generally moving electric charges, create magnetic fields (see Maxwell's Equations).
- Many particles have nonzero "intrinsic" (or "spin") magnetic moments. (Just as each particle, by its nature, has a certain mass and charge, each has a certain magnetic moment, possibly zero.)
In magnetic materials, the most important sources of magnetization are, more specifically, the electrons' orbital angular motion around the nucleus, and the electrons' intrinsic magnetic moment (see Electron magnetic dipole moment). The other potential sources of magnetism are much less important: For example, the nuclear magnetic moments of the nuclei in the material are typically thousands of times smaller than the electrons' magnetic moments, so they are negligible in the context of the magnetization of materials. (Nuclear magnetic moments are important in other contexts, particularly in Nuclear Magnetic Resonance (NMR) and Magnetic Resonance Imaging (MRI).)
Ordinarily, the countless electrons in a material are arranged such that their magnetic moments (both orbital and intrinsic) cancel out. This is due, to some extent, to electrons combining into pairs with opposite intrinsic magnetic moments (as a result of the Pauli exclusion principle; see Electron configuration), or combining into "filled subshells" with zero net orbital motion; in both cases, the electron arrangement is so as to exactly cancel the magnetic moments from each electron. Moreover, even when the electron configuration is such that there are unpaired electrons and/or non-filled subshells, it is often the case that the various electrons in the solid will contribute magnetic moments that point in different, random directions, so that the material will not be magnetic.
However, sometimes (either spontaneously, or owing to an applied external magnetic field) each of the electron magnetic moments will be, on average, lined up. Then the material can produce a net total magnetic field, which can potentially be quite strong.
The magnetic behavior of a material depends on its structure (particularly its electron configuration, for the reasons mentioned above), and also on the temperature (at high temperatures, random thermal motion makes it more difficult for the electrons to maintain alignment).
[edit] Physics of paramagnetism
In a paramagnetic material there are unpaired electrons, i.e. atomic or molecular orbitals with exactly one electron in them. While paired electrons are required by the Pauli exclusion principle to have their intrinsic ('spin') magnetic moments pointing in opposite directions, causing their magnetic fields to cancel out, an unpaired electron is free to align its magnetic moment in any direction. When an external magnetic field is applied, these magnetic moments will tend to align themselves in the same direction as the applied field, thus reinforcing it.
[edit] Physics of diamagnetism
In a diamagnetic material, there are no unpaired electrons, so the intrinsic electron magnetic moments cannot produce any bulk effect. In these cases, the magnetization arises from the electrons' orbital motions, which can be understood classically as follows:
When a material is put in a magnetic field, the electrons circling the nucleus will experience, in addition to their Coulomb attraction to the nucleus, a Lorentz force from the magnetic field. Depending on which direction the electron is orbiting, this force may increase the centripetal force on the electrons, pulling them in towards the nucleus, or it may decrease the force, pulling them away from the nucleus. This effect systematically increases the orbital magnetic moments that were aligned opposite the field, and decreases the ones aligned parallel to the field (in accordance with Lenz's law). This results in a small bulk magnetic moment, with an opposite direction to the applied field.
Note that this description is meant only as an heuristic; a proper understanding requires a quantum-mechanical description.
Note that all materials undergo this orbital response. However, in paramagnetic and ferromagnetic substances, the diamagnetic effect is overwhelmed by the much stronger effects caused by the unpaired electrons.
[edit] Physics of ferromagnetism
A ferromagnet, like a paramagnetic substance, has unpaired electrons. However, in addition to the electrons' intrinsic magnetic moments wanting to be parallel to an applied field, there is also in these materials a tendency for these magnetic moments to want to be parallel to each other. Thus, even when the applied field is removed, the electrons in the material can keep each other continually pointed in the same direction.
Every ferromagnetic substance has its own individual temperature, called the Curie temperature, or Curie point, above which it loses its ferromagnetic properties. This is because the thermal tendency to disorder overwhelms the energy-lowering due to ferromagnetic order.
[edit] Magnetic domains
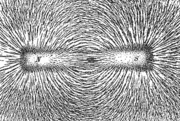
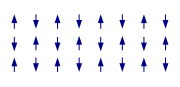
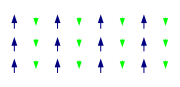
The magnetic moment of atoms in a ferromagnetic material cause them to behave something like tiny permanent magnets. They stick together and align themselves into small regions of more or less uniform alignment called magnetic domains or Weiss domains. Magnetic domains can be observed with a magnetic force microscope to reveal magnetic domain boundaries that resemble white lines in the sketch.There are many scientific experiments that can physically show magnetic fields.
When a domain contains too many molecules, it becomes unstable and divides into two domains aligned in opposite directions so that they stick together more stably as shown at the right.
When exposed to a magnetic field, the domain boundaries move so that the domains aligned with the magnetic field grow and dominate the structure as shown at the left. When the magnetizing field is removed, the domains may not return to a unmagnetized state. This results in the ferromagnetic material being magnetized, forming a permanent magnet.
When magnetized strongly enough that the prevailing domain overruns all others to result in only one single domain, the material is magnetically saturated. When a magnetized ferromagnetic material is heated to the Curie point temperature, the molecules are agitated to the point that the magnetic domains lose the organization and the magnetic properties they cause cease. When the material is cooled, this domain alignment structure spontaneously returns, in a manner roughly analogous to how a liquid can freeze into a crystalline solid.
[edit] Physics of antiferromagnetism
In an antiferromagnet, unlike a ferromagnet, there is a tendency for the intrinsic magnetic moments of neighboring valence electrons to point in opposite directions. When all atoms are arranged in a substance so that each neighbor is 'anti-aligned', the substance is antiferromagnetic. Antiferromagnets have a zero net magnetic moment, meaning no field is produced by them. Antiferromagnets are less common compared to the other types of behaviors, and are mostly observed at low temperatures. In varying temperatures, antiferromagnets can be seen to exhibit diamagnetic and ferrimagnetic properties.
In some materials, neighboring electrons want to point in opposite directions, but there is no geometrical arrangement in which each pair of neighbors is anti-aligned. This is called a spin glass, and is an example of geometrical frustration.
Physics of ferrimagnetism
Like ferromagnetism, ferrimagnets retain their magnetization in the absence of a field. However, like antiferromagnets, neighboring pairs of electron spins like to point in opposite directions. These two properties are not contradictory, because in the optimal geometrical arrangement, there is more magnetic moment from the sublattice of electrons which point in one direction, than from the sublattice which points in the opposite direction.
The first discovered magnetic substance, magnetite, was originally believed to be a ferromagnet; Louis Néel disproved this, however, with the discovery of ferrimagnetism.
[edit] Other types of magnetism
There are various other types of magnetism, such as spin glass (mentioned above), superparamagnetism, superdiamagnetism, and metamagnetism.
[edit] Common uses of magnets
- Magnetic recording media: VHS tapes contain a reel of magnetic tape. The information that makes up the video and sound is encoded on the magnetic coating on the tape. Common audio cassettes also rely on magnetic tape. Similarly, in computers, floppy disks and hard disks record data on a thin magnetic coating.
- Credit, debit, and ATM cards: All of these cards have a magnetic strip on one side. This strip encodes the information to contact an individual's financial institution and connect with their account(s).
- Common televisions and computer monitors: TV and computer screens containing a cathode ray tube employ an electromagnet to guide electrons to the screen. Plasma screens and LCDs use different technologies.
- Speakers and Microphones: Most speakers employ a permanent magnet and a current-carrying coil to convert electric energy (the signal) into mechanical energy (movement which creates the sound). The coil is wrapped around a bobbin attached to the speaker cone, and carries the signal as changing current which interacts with the field of the permanent magnet. The voice coil feels a magnetic force and in response moves the cone and pressurizes the neighboring air, thus generating sound. Dynamic microphones employ the same concept, but in reverse. A microphone has a diaphragm or membrane attached to a coil of wire. The coil rests inside a specially shaped magnet. When sound vibrates the membrane, the coil is vibrated as well. As the coil moves through the magnetic field, a voltage is induced across the coil. This voltage drives a current in the wire that is characteristic of the original sound.
- Electric motors and generators: Some electric motors (much like loudspeakers) rely upon a combination of an electromagnet and a permanent magnet, and much like loudspeakers, they convert electric energy into mechanical energy. A generator is the reverse: it converts mechanical energy into electric energy by moving a conductor through a magnetic field.
- Transformers: Transformers are devices that transfer electric energy between two windings of wire that are electrically isolated but are coupled magnetically.
- Chucks: Chucks are used in the metalworking field to hold objects. Magnets are also used in other types of fastening devices, such as the magnetic base, the magnetic clamp and the refrigerator magnet.
- Compasses: A compass (or mariner's compass) is a magnetized pointer free to align itself with a magnetic field, most commonly Earth's magnetic field.
- Art: Vinyl magnet sheets may be attached to paintings, photographs, and other ornamental articles, allowing them to be attached to refrigerators and other metal surfaces.
- Science Projects: Many topic questions are based on magnets. For example: how is the strength of a magnet affected by glass, plastic, and cardboard?
- Toys: Given their ability to counteract the force of gravity at close range, magnets are often employed in children's toys such as the Magnet Space Wheel to amusing effect.
- Magnets can be used to make jewellery. Necklaces and bracelets can have a magnetic clasp, or may be constructed entirely from a linked series of magnets and ferrous beads.
- Magnets can pick up magnetic items (iron nails, staples, tacks, paper clips) that are either too small, too hard to reach, or too thin for fingers to hold. Some screwdrivers are magnetized for this purpose.
- Magnets can be used in scrap and salvage operations to separate magnetic metals (iron, steel, and nickel) from non-magnetic metals (aluminum, non-ferrous alloys, etc.). The same idea can be used in the so-called "magnet test", in which an auto body is inspected with a magnet to detect areas repaired using fiberglass or plastic putty.
- Magnetic levitation transport, or maglev, is a form of transportation that suspends, guides and propels vehicles (especially trains) through electromagnetic force. The maximum recorded speed of a maglev train is 581 kilometres per hour (361 mph).
- Magnets may be used to connect some cables to serve as a fail-safe if the cord is pulled.
[edit] Medical issues and safety
Because human tissues have a very low level of susceptibility to static magnetic fields, there is no scientific evidence showing a health hazard associated with exposure to these fields. However, if a ferromagnetic foreign body is present in human tissue, the magnetic field will interact with it, which can pose a serious safety risk.[3]
Specifically, if a pacemaker has been embedded in a patient's chest (usually for the purpose of monitoring and regulating the heart for steady electrically induced beats), care should be taken to keep it away from magnetic fields. It is for this reason that a patient with the device installed cannot be tested with the use of an MRI, which is a magnetic imaging device.
Children sometimes swallow small magnets from toys; and this can be hazardous if two or more magnets are swallowed, as the magnets can pinch or puncture internal tissues; one death has been reported.[4]
[edit] Magnetization and demagnetization
Ferromagnetic materials can be magnetized in the following ways:
- Heating the object above its Curie temperature, allowing it to cool in a magnetic field and hammering it as it cools. This is the most effective method, and is similar to the industrial processes used to create permanent magnets.
- Placing the item in an external magnetic field will result in the item retaining some of the magnetism on removal. Vibration has been shown to increase the effect. Ferrous materials aligned with the earth's magnetic field and which are subject to vibration (e.g. frame of a conveyor) have been shown to acquire significant residual magnetism. A magnetic field much stronger than the earth's can be generated inside a solenoid by passing direct current through it.
- Stroking - An existing magnet is moved from one end of the item to the other repeatedly in the same direction.
Magnetized materials can be demagnetized in the following ways:
- Heating a magnet past its Curie temperature - the molecular motion destroys the alignment of the magnetic domains. This always removes all magnetization.
- Hammering or jarring - the mechanical disturbance tends to randomize the magnetic domains. Will leave some residual magnetization.
- Placing the magnet in an alternating magnetic field, such as that generated by a solenoid with an alternating current through it, and then either slowly drawing the magnet out or slowly decreasing the magnetic field to zero. This is the principle used in commercial demagnetizers to demagnetize tools and erase credit cards and hard disks, and degaussing coils used to demagnetize CRTs.
[edit] Types of permanent magnets
[edit] Magnetic metallic elements
Many materials have unpaired electron spins, and the majority of these materials are paramagnetic. When the spins interact with each other in such a way that the spins align spontaneously, the materials are called ferromagnetic (what is often loosely termed as "magnetic"). Because of the way their regular crystalline atomic structure causes their spins to interact, some metals are (ferro)magnetic when found in their natural states, as ores. These include iron ore (magnetite or lodestone), cobalt and nickel, as well the rare earth metals gadolinium and dysprosium (when at a very low temperature). Such naturally occurring (ferro)magnets were used in the first experiments with magnetism. Technology has since expanded the availability of magnetic materials to include various manmade products, all based, however, on naturally magnetic elements.
[edit] Composites
[edit] Ceramic or ferrite
Ceramic, or ferrite, magnets are made of a sintered composite of powdered iron oxide and barium/strontium carbonate ceramic. Given the low cost of the materials and manufacturing methods, inexpensive magnets (or nonmagnetized ferromagnetic cores, for use in electronic component such as radio antennas, for example) of various shapes can be easily mass-produced. The resulting magnets are noncorroding, but brittle and must be treated like other ceramics.
[edit] Alnico
Alnico magnets are made by casting or sintering a combination of aluminium, nickel and cobalt with iron and small amounts of other elements added to enhance the properties of the magnet. Sintering offers superior mechanical characteristics, whereas casting delivers higher magnetic fields and allows for the design of intricate shapes. Alnico magnets resist corrosion and have physical properties more forgiving than ferrite, but not quite as desirable as a metal.
[edit] Ticonal
Ticonal magnets are an alloy of titanium, cobalt, nickel, and aluminum, with iron and small amounts of other elements. It was developed by Philips for loudspeakers.
[edit] Injection molded
Injection molded magnets are a composite of various types of resin and magnetic powders, allowing parts of complex shapes to be manufactured by injection molding. The physical and magnetic properties of the product depend on the raw materials, but are generally lower in magnetic strength and resemble plastics in their physical properties.
[edit] Flexible
Flexible magnets are similar to injection molded magnets, using a flexible resin or binder such as vinyl, and produced in flat strips, shapes or sheets. These magnets are lower in magnetic strength but can be very flexible, depending on the binder used. Flexible magnets can be used in industrial printers.
[edit] Rare earth magnets
'Rare earth' (lanthanoid) elements have a partially occupied f electron shell (which can accommodate up to 14 electrons.) The spin of these electrons can be aligned, resulting in very strong magnetic fields, and therefore these elements are used in compact high-strength magnets where their higher price is not a concern. The most common types of rare earth magnets are samarium-cobalt and neodymium-iron-boron (NIB) magnets.
[edit] Single-molecule magnets (SMMs) and single-chain magnets (SCMs)
In the 1990s it was discovered that certain molecules containing paramagnetic metal ions are capable of storing a magnetic moment at very low temperatures. These are very different from conventional magnets that store information at a "domain" level and theoretically could provide a far denser storage medium than conventional magnets. In this direction research on monolayers of SMMs is currently under way. Very briefly, the two main attributes of an SMM are:
- a large ground state spin value (S), which is provided by ferromagnetic or ferrimagnetic coupling between the paramagnetic metal centres.
- a negative value of the anisotropy of the zero field splitting (D)
Most SMM's contain manganese, but can also be found with vanadium, iron, nickel and cobalt clusters. More recently it has been found that some chain systems can also display a magnetization which persists for long times at relatively higher temperatures. These systems have been called single-chain magnets.
[edit] Nano-structured magnets
Some nano-structured materials exhibit energy waves called magnons that coalesce into a common ground state in the manner of a Bose-Einstein condensate.[5][6]
[edit] Costs
The current[update] cheapest permanent magnets, allowing for field strengths, are flexible and ceramic magnets, but these are also among the weakest types. Neodymium-iron-boron (NIB) magnets are among the strongest. These cost more per kilogram than most other magnetic materials, but owing to their intense field, are smaller and cheaper in many applications.[7]
[edit] Temperature
Temperature sensitivity varies, but when a magnet is heated to a temperature known as the Curie point, it loses all of its magnetism, even after cooling below that temperature. The magnets can often be remagnetised however. Additionally some magnets are brittle and can fracture at high temperatures.
[edit] Electromagnets
An electromagnet in its simplest form, is a wire that has been coiled into one or more loops, known as a solenoid. When electric current flows through the wire, a magnetic field is generated. It is concentrated near (and especially inside) the coil, and its field lines are very similar to those for a magnet. The orientation of this effective magnet is determined by the right hand rule. The magnetic moment and the magnetic field of the electromagnet are proportional to the number of loops of wire, to the cross-section of each loop, and to the current passing through the wire.
If the coil of wire is wrapped around a material with no special magnetic properties (e.g., cardboard), it will tend to generate a very weak field. However, if it is wrapped around a "soft" ferromagnetic material, such as an iron nail, then the net field produced can result in a several hundred- to thousandfold increase of field strength.
Uses for electromagnets include particle accelerators, electric motors, junkyard cranes, and magnetic resonance imaging machines. Some applications involve configurations more than a simple magnetic dipole, for example quadrupole and sextupole magnets are used to focus particle beams.
[edit] Units and calculations in magnetism
For most engineering applications, MKS (rationalized) or SI (Système International) is common. Two other sets, Gaussian and CGS-emu, are the same for magnetic properties, and are commonly used in physics.
In all units it is convenient to employ two types of magnetic field, B and H, as well as the magnetization M, defined as the magnetic moment per unit volume.
- The magnetic induction field B is given in SI units of teslas (T). B is the true magnetic field, whose time variation produces, by Faraday's Law, circulating electric fields (which the power companies sell). B also produces a deflection force on moving charged particles (as in TV tubes). The tesla is equivalent to the magnetic flux (in webers) per unit area (in meters squared), thus giving B the unit of a flux density. In CGS the unit of B is the gauss (G). One tesla equals 104 G.
- The magnetic field H is given in SI units of ampere-turns per meter (A-turn/m). The "turns" appears because when H is produced by a current-carrying wire, its value is proportional to the number of turns of that wire. In CGS the unit of H is the oersted (Oe). One A-turn/m equals 4π x 10-3 Oe.
- The magnetization M is given in SI units of amperes per meter (A/m). In CGS the unit of M is the emu, or electromagnetic unit[vague]. One A/m equals 10-3 emu. A good permanent magnet can have a magnetization as large as a million amperes per meter. Magnetic fields produced by current-carrying wires would require comparably huge currents per unit length, one reason we employ permanent magnets and electromagnets.
- In SI units, the relation B = μ0(H + M) holds, where μ0 is the permeability of space, which equals 4π x 10-7 tesla meters per ampere. In CGS it is written as B = H + 4πM. [The pole approach gives μ0H in SI units. A μ0M term in SI must then supplement this μ0H to give the correct field within B the magnet. It will agree with the field B calculated using Amperian currents.]
Materials that are not permanent magnets usually satisfy the relation M = χH in SI, where χ is the (dimensionless) magnetic susceptibility. Most non-magnetic materials have a relatively small χ (on the order of a millionth), but soft magnets can have χ on the order of hundreds or thousands. For materials satisfying M = χH, we can also write B = μ0(1 + χ)H = μ0μrH = μH, where μr = 1 + χ is the (dimensionless) relative permeability and μ = μ0μr is the magnetic permeability. Both hard and soft magnets have a more complex, history-dependent, behavior described by what are called hysteresis loops, which give either B vs H or M vs H. In CGS M = χH, but χSI = 4πχCGS, and μ = μr.
Caution: In part because there are not enough Roman and Greek symbols, there is no commonly agreed upon symbol for magnetic pole strength and magnetic moment. The symbol m has been used for both pole strength (unit = A·m, where here the upright m is for meter) and for magnetic moment (unit = A·m²). The symbol μ has been used in some texts for magnetic permeability and in other texts for magnetic moment. We will use μ for magnetic permeability and m for magnetic moment. For pole strength we will employ qm. For a bar magnet of cross-section A with uniform magnetization M along its axis, the pole strength is given by qm = MA, so that M can be thought of as a pole strength per unit area.
[edit] Fields of a magnet
Far away from a magnet, the magnetic field created by that magnet is almost always described (to a good approximation) by a dipole field characterized by its total magnetic moment. This is true regardless of the shape of the magnet, so long as the magnetic moment is nonzero. One characteristic of a dipole field is that the strength of the field falls off inversely with the cube of the distance from the magnet's center.
Closer to the magnet, the magnetic field becomes more complicated, and more dependent on the detailed shape and magnetization of the magnet. Formally, the field can be expressed as a multipole expansion: A dipole field, plus a quadrupole field, plus an octupole field, etc.
At close range, many different fields are possible. For example, for a long, skinny bar magnet with its north pole at one end and south pole at the other, the magnetic field near either end falls off inversely with the square of the distance from that pole.
[edit] Calculating the magnetic force
Calculating the attractive or repulsive force between two magnets is, in the general case, an extremely complex operation, as it depends on the shape, magnetization, orientation and separation of the magnets.
[edit] Force between two magnetic poles
The force between two magnetic poles is given by:
where
- F is force (SI unit: newton)
- qm1 and qm2 are the magnitudes of magnetic poles (SI unit: ampere meter)
- μ is the permeability of the intervening medium (SI unit: tesla meter per ampere, henry per meter or newton per ampere squared)
- r is the separation (SI unit: meter).
The pole description is useful to practicing magneticians who design real-world magnets, but real magnets have a pole distribution more complex than a single north and south. Therefore, implementation of the pole idea is not simple. In some cases, one of the more complex formulae given below will be more useful.
[edit] Force between two nearby attracting surfaces of area A and equal but opposite magnetizations M
where
- A is the area of each surface, in m²
- M is their magnetization, in A/m.
- μ0 is the permeability of space, which equals 4π x 10-7 tesla-meters per ampere
[edit] Force between two bar magnets
The force between two identical cylindrical bar magnets placed end to end is given by:
where
- B0 is the magnetic flux density very close to each pole, in T,
- A is the area of each pole, in m2,
- L is the length of each magnet, in m,
- R is the radius of each magnet, in m, and
- x is the separation between the two magnets, in m
B0 = M relates the flux density at the pole to the magnetization of the magnet.
M relates the flux density at the pole to the magnetization of the magnet.
[edit] Footnotes and in-line references
- ^ Knight, Jones, & Field, "College Physics" (2007) p. 815
- ^ Griffiths, David J. (1998). Introduction to Electrodynamics (3rd ed.). Prentice Hall. ISBN 0-13-805326-X., section 6.1.
- ^ Schenck JF (2000). "Safety of strong, static magnetic fields". J Magn Reson Imaging 12 (1): 2–19. doi:. PMID 10931560.
- ^ Oestreich AE (2008). "Worldwide survey of damage from swallowing multiple magnets". Pediatr Radiol. doi:. PMID 19020871.
- ^ "Nanomagnets Bend The Rules". http://www.spacedaily.com/news/nanotech-05zm.html. Retrieved on November 14 2005.
- ^ Della Torre, E. (2005). "Extension of the Bloch T3/2 Law to Magnetic Nanostructures: Bose-Einstein Condensation". Physical Review Letters 94 (14): 147210. doi:.
- ^ Magnet sales- Frequently Asked Questions
[edit] Online references
- HyperPhysics E/M, good complete tree diagram of electromagnetic relationships with magnets
- Maxwell's Equations and some history...
- Detailed Theory on Designing a Solenoid or a Coil Gun
[edit] Printed references
1. "positive pole n." The Concise Oxford English Dictionary. Ed. Catherine Soanes and Angus Stevenson. Oxford University Press, 2004. Oxford Reference Online. Oxford University Press.
2. Wayne M. Saslow, "Electricity, Magnetism, and Light", Academic (2002). ISBN 0-12-619455-6. Chapter 9 discusses magnets and their magnetic fields using the concept of magnetic poles, but it also gives evidence that magnetic poles do not really exist in ordinary matter. Chapters 10 and 11, following what appears to be a 19th century approach, use the pole concept to obtain the laws describing the magnetism of electric currents.
3. Edward P. Furlani, "Permanent Magnet and Electromechanical Devices: Materials, Analysis and Applications", Academic Press Series in Electromagnetism (2001). ISBN 0-12-269951-3.
[edit] External links
- Articles, tutorials and other educational information about magnets National High Magnetic Field Laboratory
- Answers to several questions from curious kids about magnets
- Magnetic units are discussed here
- EU requires warning on toys containing magnets
- Information on Permanent Magnets
[edit] See also
|
|
| Look up magnet in Wiktionary, the free dictionary. |
|
|||||









![F=\left[\frac {B_0^2 A^2 \left( L^2+R^2 \right)} {\pi\mu_0L^2}\right] \left[{\frac 1 {x^2}} + {\frac 1 {(x+2L)^2}} - {\frac 2 {(x+L)^2}} \right]](http://upload.wikimedia.org/math/e/a/0/ea0c076f1c59249aba590d07b31da41e.png)

