Truth table
From Wikipedia, the free encyclopedia
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, boolean functions, and propositional calculus—to compute the functional values of logical expressions on each of their functional arguments, that is, on each combination of values taken by their logical variables (Enderton 2001). In particular, truth tables can be used to tell whether a propositional expression is true for all legitimate input values, that is, logically valid.
Contents |
[edit] Overview
The pattern of reasoning that the truth table tabulates was Frege's, Peirce's, and Schröder's by 1880. The tables have been prominent in literature since 1920 (Lukasiewicz, Post, Wittgenstein)" (Quine, 39). Lewis Carroll had formulated truth tables as early as 1894 to solve certain problems, but his manuscripts containing his work on the subject were not discovered until 1977 [1]. Wittgenstein's Tractatus Logico-Philosophicus uses them to place truth functions in a series. The wide influence of this work led to the spread of the use of truth tables.
Truth tables are used to compute the values of propositional expressions in an effective manner that is sometimes referred to as a decision procedure. A propositional expression is either an atomic formula—a propositional constant, propositional variable, or propositional function term (for example, Px or P(x))—or built up from atomic formulas by means of logical operators, for example, AND ( ), OR (
), OR (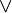 ), NOT (
), NOT ( ). For instance,
). For instance,  is a propositional expression.
is a propositional expression.
The column headings on a truth table show (i) the propositional functions and/or variables, and (ii) the truth-functional expression built up from those propositional functions or variables and operators. The rows show each possible valuation of T or F assignments to (i) and (ii). In other words, each row is a distinct interpretation of (i) and (ii).
Truth tables for classical logic are limited to Boolean logical systems in which only two logical values are possible, false and true, usually written F and T, or sometimes 0 or 1, respectively.
[edit] Logical operations
[edit] Logical negation
Logical negation is an operation on one logical value, typically the value of a proposition, that produces a value of true if its operand is false and a value of false if its operand is true.
The truth table for NOT p (also written as ~p or ¬p) is as follows:
| p |  |
|---|---|
| T | F |
| F | T |
[edit] Logical conjunction
Logical conjunction is an operation on two logical values, typically the values of two propositions, that produces a value of true if and only if both of its operands are true.
The truth table for p AND q (also written as p ∧ q, p & q, or p q) is as follows:
q) is as follows:
| p | q | p . q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
In ordinary language terms, if both p and q are true, then the conjunction p ∧ q is true. For all other assignments of logical values to p and to q the conjunction p ∧ q is false.
It can also be said that if p, then p ∧ q is q, otherwise p ∧ q is p.
[edit] Logical disjunction
Logical disjunction is an operation on two logical values, typically the values of two propositions, that produces a value of false if and only if both of its operands are false.
The truth table for p OR q (also written as p ∨ q, p || q, or p + q) is as follows:
| p | q | p + q |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
Stated in English, if p, then p ∨ q is p, otherwise p ∨ q is q.
[edit] Logical implication
Logical implication and the material conditional are both associated with an operation on two logical values, typically the values of two propositions, that produces a value of false just in the singular case the first operand is true and the second operand is false.
The truth table associated with the material conditional not p or q (symbolized as p → q) and the logical implication p implies q (symbolized as p ⇒ q) is as follows:
| p | q | p → q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
If T=1 and F=0 and the base is 2 and 1 being the maximum 1+1=1 1+0=1 0+1=1 0+0=0
[edit] Logical equality
Logical equality (also known as biconditional) is an operation on two logical values, typically the values of two propositions, that produces a value of true if and only if both operands are false or both operands are true.
The truth table for p EQ q (also written as p = q, p ↔ q, or p ≡ q) is as follows:
| p | q | p ≡ q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
a) If the truth leads to the truth, the result is the truth b) If the truth leads to falsity, then the result is false c) If falsity leads to the truth, then the result is the truth d) If falsity leads to falsity, then the logic is true, because falsity leading to falsity will not lead to the truth
[edit] Exclusive disjunction
Exclusive disjunction is an operation on two logical values, typically the values of two propositions, that produces a value of true if and only if one but not both of its operands is true.
The truth table for p XOR q (also written as p + q, p ⊕ q, or p ≠ q) is as follows:
| p | q | p ⊕ q |
|---|---|---|
| T | T | F |
| T | F | T |
| F | T | T |
| F | F | F |
For two propositions, XOR can also be written as (p = 1 ∧ q = 0)∨ (p = 0 ∧ q = 1).
[edit] Logical NAND
The logical NAND is an operation on two logical values, typically the values of two propositions, that produces a value of false if and only if both of its operands are true. In other words, it produces a value of true if and only if at least one of its operands is false.
The truth table for p NAND q (also written as p | q or p ↑ q) is as follows:
| p | q | p ↑ q |
|---|---|---|
| T | T | F |
| T | F | T |
| F | T | T |
| F | F | T |
It is frequently useful to express a logical operation as a compound operation, that is, as an operation that is built up or composed from other operations. Many such compositions are possible, depending on the operations that are taken as basic or "primitive" and the operations that are taken as composite or "derivative".
In the case of logical NAND, it is clearly expressible as a compound of NOT and AND.
The negation of conjunction  , and the disjunction of negations
, and the disjunction of negations  are depicted as follows:
are depicted as follows:
| p | q |  |
 |
 |
 |
 |
|---|---|---|---|---|---|---|
| T | T | T | F | F | F | F |
| T | F | F | T | F | T | T |
| F | T | F | T | T | F | T |
| F | F | F | T | T | T | T |
[edit] Logical NOR
The logical NOR is an operation on two logical values, typically the values of two propositions, that produces a value of true if and only if both of its operands are false. In other words, it produces a value of false if and only if at least one of its operands is true. ↓ is also known as the Peirce arrow after its inventor, Charles Peirce, and is a Sole sufficient operator.
The truth table for p NOR q (also written as p ⊥ q or p ↓ q) is as follows:
| p | q | p ↓ q |
|---|---|---|
| T | T | F |
| T | F | F |
| F | T | F |
| F | F | T |
The negation of disjunction  and the conjunction of negations
and the conjunction of negations  are tabulated as follows:
are tabulated as follows:
| p | q |  |
 |
 |
 |
 |
|---|---|---|---|---|---|---|
| T | T | T | F | F | F | F |
| T | F | T | F | F | T | F |
| F | T | T | F | T | F | F |
| F | F | F | T | T | T | T |
Inspection of the tabular derivations for NAND and NOR, under each assignment of logical values to the functional arguments  and
and 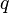 , produces the identical patterns of functional values for
, produces the identical patterns of functional values for  as for
as for  , and for
, and for  as for
as for  . Thus the first and second expressions in each pair are logically equivalent, and may be substituted for each other in all contexts that pertain solely to their logical values.
. Thus the first and second expressions in each pair are logically equivalent, and may be substituted for each other in all contexts that pertain solely to their logical values.
This equivalence is one of De Morgan's laws.
[edit] Applications
Truth tables can be used to prove many other logical equivalences. For example, consider the following truth table:
| p | q | ¬p | ¬p ∨ q | p → q |
|---|---|---|---|---|
| F | F | T | T | T |
| F | T | T | T | T |
| T | F | F | F | F |
| T | T | F | T | T |
This demonstrates the fact that p → q is logically equivalent to ¬p ∨ q.
[edit] Truth table for most commonly used logical operators
Here is a truth table giving definitions of the most commonly used 6 of the 16 possible truth functions of 2 binary variables (P,Q are thus boolean variables):
| P | Q | 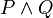 |
 |
 |
 |
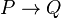 |
 |
|---|---|---|---|---|---|---|---|
| F | F | F | F | F | T | T | T |
| F | T | F | T | T | F | T | F |
| T | F | F | T | T | F | F | T |
| T | T | T | T | F | T | T | T |
Key:
- T = true, F = false
 = AND (logical conjunction)
= AND (logical conjunction) = OR (logical disjunction)
= OR (logical disjunction) = XOR (exclusive or)
= XOR (exclusive or) = XNOR (exclusive nor)
= XNOR (exclusive nor) = conditional "if-then"
= conditional "if-then" = conditional "(then)-if"
= conditional "(then)-if"
 biconditional or "if-and-only-if" is logically equivalent to
biconditional or "if-and-only-if" is logically equivalent to  : XNOR (exclusive nor).
: XNOR (exclusive nor).
Johnston diagrams, similar to Venn diagrams and Euler diagrams, provide a way of visualizing truth tables. An interactive Johnston diagram illustrating truth tables is at LogicTutorial.com
[edit] Condensed truth tables for binary operators
For binary operators, a condensed form of truth table is also used, where the row headings and the column headings specify the operands and the table cells specify the result. For example Boolean logic uses this condensed truth table notation:
|
|
This notation is useful especially if the operations are commutative, although one can additionally specify that the rows are the first operand and the columns are the second operand. This condensed notation is particularly useful in discussing multi-valued extensions of logic, as it significantly cuts down on combinatoric explosion of the number of rows otherwise needed. It also provides for quickly recognizable characteristic "shape" of the distribution of the values in the table which can assist the reader in grasping the rules more quickly.
[edit] Truth tables in digital logic
Truth tables are also used to specify the functionality of hardware look-up tables (LUTs) in digital logic circuitry. For an n-input LUT, the truth table will have 2^n values (or rows in the above tabular format), completely specifying a boolean function for the LUT. By representing each boolean value as a bit in a binary number, truth table values can be efficiently encoded as integer values in electronic design automation (EDA) software. For example, a 32-bit integer can encode the truth table for a LUT with up to 5 inputs.
When using an integer representation of a truth table, the output value of the LUT can be obtained by calculating a bit index k based on the input values of the LUT, in which case the LUT's output value is the kth bit of the integer. For example, to evaluate the output value of a LUT given an array of n boolean input values, the bit index of the truth table's output value can be computed as follows: if the ith input is true, let Vi = 1, else let Vi = 0. Then the kth bit of the binary representation of the truth table is the LUT's output value, where k = V0*2^0 + V1*2^1 + V2*2^2 + ... + Vn*2^n.
Truth tables are a simple and straightforward way to encode boolean functions, however given the exponential growth in size as the number of inputs increase, they are not suitable for functions with a large number of inputs. Other representations which are more memory efficient are text equations and binary decision diagrams.
[edit] Applications of truth tables in digital electronics
In digital electronics (and computer science, fields of engineering derived from applied logic and math), truth tables can be used to reduce basic boolean operations to simple correlations of inputs to outputs, without the use of logic gates or code. For example, a binary addition can be represented with the truth table:
A B | C R 1 1 | 1 0 1 0 | 0 1 0 1 | 0 1 0 0 | 0 0 where A = First Operand B = Second Operand C = Carry R = Result
This truth table is read left to right:
- Value pair (A,B) equals value pair (C,R).
- Or for this example, A plus B equal result R, with the Carry C.
Note that this table does not describe the logic operations necessary to implement this operation, rather it simply specifies the function of inputs to output values.
In this case it can only be used for very simple inputs and outputs, such as 1's and 0's, however if the number of types of values one can have on the inputs increases, the size of the truth table will increase.
For instance, in an addition operation, one needs two operands, A and B. Each can have one of two values, zero or one. The number of combinations of these two values is 2x2, or four. So the result is four possible outputs of C and R. If one was to use base 3, the size would increase to 3x3, or nine possible outputs.
The first "addition" example above is called a half-adder. A full-adder is when the carry from the previous operation is provided as input to the next adder. Thus, a truth table of eight rows would be needed to describe a full adder's logic:
A B C* | C R 0 0 0 | 0 0 0 1 0 | 0 1 1 0 0 | 0 1 1 1 0 | 1 0 0 0 1 | 0 1 0 1 1 | 1 0 1 0 1 | 1 0 1 1 1 | 1 1 Same as previous, but.. C* = Carry from previous adder
[edit] See also
|
[edit] References
- Enderton, H. (2001). A Mathematical Introduction to Logic, second edition, Harcourt Academic Press. ISBN 0-12-238452-0
- Quine, W.V. (1982), Methods of Logic, 4th edition, Harvard University Press, Cambridge, MA.
[edit] External links
| Wikimedia Commons has media related to: Truth tables |
- Online Truth Table Generator
- Web-based truth table generator
- Powerful logic engine
- Boolean expression evaluator, generates truth table (Java applet)
- Free logic minimization program Minilog
- Samuel Williams' Truth Table Evaluator
|
|||||||||||||||||||


