Gamma function
From Wikipedia, the free encyclopedia
In mathematics, the Gamma function (represented by the capitalized Greek letter Γ) is an extension of the factorial function to real and complex numbers. For a complex number z with positive real part the Gamma function is defined by
This definition can be extended to the rest of the complex plane, excepting the non-positive integers.
If n is a positive integer, then
- Γ(n) = (n − 1)!,
showing the connection to the factorial function. The Gamma function generalizes the factorial function for non-integer and complex values of n.
The Gamma function is a component in various probability-distribution functions, and as such it is applicable in the fields of probability and statistics, as well as combinatorics.
Contents |
[edit] Definition
[edit] Main definition
The notation Γ(z) is due to Adrien-Marie Legendre. If the real part of the complex number z is positive (Re[z] > 0), then the integral
converges absolutely. Using integration by parts, one can show that
This functional equation generalizes the relation  of the factorial function. We can evaluate Γ(1) analytically:
of the factorial function. We can evaluate Γ(1) analytically:
Combining these two relations shows how the factorial function is a special case of the Gamma function:
for all natural numbers n.

The identity (1) can also be used to extend Γ(z), by analytic continuation, to a meromorphic function defined for all complex numbers z except 0 and the negative integers (it can be calculated that z = − n is a simple pole with residue ( − 1)n / n!).[1] It is this extended version that is commonly referred to as the Gamma function.
[edit] Alternative definitions
The following infinite product definitions for the Gamma function, due to Euler and Weierstrass respectively, are valid for all complex numbers z, except 0 and the negative integers:
where γ is the Euler–Mascheroni constant.
It is straightforward to show that the Euler definition satisfies the functional equation (1) above, as follows. Provided z is not equal to 0, -1, -2, ...
In a different way it can be shown that...
A somewhat curious parametrization of the Gamma function is given in terms of Laguerre polynomials,
 which converges for
which converges for 
[edit] Derivation of relationship with factorials using integration by parts
Finding Γ(1) is easy:

Next, we derive an expression for Γ(n + 1) as a function of Γ(n):

We use integration by parts to solve this integral
![\int_0^\infty e^{-x} x ^n dx = \left[\frac{-x^n}{e^x}\right]_0^\infty + n \int_0^\infty e^{-x} x ^{n - 1} dx](http://upload.wikimedia.org/math/9/1/7/9176c967bc5113089b2be4d98199beac.png)
We can see that  .
.
At infinity, we have, by L'Hôpital's rule,
 . (We have basically differentiated the top and bottom n times.)
. (We have basically differentiated the top and bottom n times.)
So the first term, ![\left[\frac{-x^n}{e^x}\right]_0^\infty](http://upload.wikimedia.org/math/d/7/7/d774d2bbd5332fbb86b57635227fc596.png) , evaluates to zero, which leaves
, evaluates to zero, which leaves

The right hand side of this equation is exactly nΓ(n). We have obtained a recurrence relation:
- Γ(n + 1) = nΓ(n).
Using this formula we derive a pattern:
The last line is really enough, as we have then proved the result by induction (The base step of the argument is easy to see, given the fact that Γ(1) = 1).
[edit] Properties
[edit] General
Other important functional equations for the Gamma function are Euler's reflection formula
and the duplication formula
The duplication formula is a special case of the multiplication theorem
A basic but useful property, which can be seen from the limit definition, is:
Perhaps the most well-known value of the Gamma function at a non-integer argument is
which can be found by setting z = 1/2 in the reflection or duplication formulas, by using the relation to the Beta function given below with x = y = 1/2, or simply by making the substitution  in the integral definition of the Gamma function, resulting in a Gaussian integral. In general, for odd integer values of n we have:
in the integral definition of the Gamma function, resulting in a Gaussian integral. In general, for odd integer values of n we have:
 (n odd)
(n odd)
 (n odd)
(n odd)
where n!! denotes the double factorial.
The derivatives of the Gamma function are described in terms of the polygamma function. For example:
For positive integer m the derivative of Gamma function can be calculated as follows (here γ is the Euler–Mascheroni constant):
The n-th derivative of the Gamma function is:
This can be derived by differentiating the integral form of the Gamma function with respect to x, and using the technique of differentiation under the integral sign.
The Gamma function has a pole of order 1 at z = −n for every natural number and zero n (z = 0, −1, −2, −3, ...); the residue there is given by
The Bohr–Mollerup theorem states that among all functions extending the factorial functions to the positive real numbers, only the Gamma function is log-convex, that is, its natural logarithm is convex.
 because:
because:
And with integration by parts:
[edit] Pi function
An alternative notation which was originally introduced by Gauss and which is sometimes used is the Pi function, which in terms of the Gamma function is
so that
Using the Pi function the reflection formula takes on the form
where sinc is the normalized sinc function, while the multiplication theorem takes on the form
We also sometimes find
which is an entire function, defined for every complex number. That π(z) is entire entails it has no poles, so Γ(z) has no zeros.
[edit] Relation to other functions
- In the first integral above, which defines the Gamma function, the limits of integration are fixed. The upper and lower incomplete Gamma functions are the functions obtained by allowing the lower or upper (respectively) limit of integration to vary.
- The Gamma function is related to the Beta function by the formula
- The derivative of the logarithm of the Gamma function is called the digamma function; higher derivatives are the polygamma functions.
- The analog of the Gamma function over a finite field or a finite ring are the Gaussian sums, a type of exponential sum.
- The reciprocal Gamma function is an entire function and has been studied as a specific topic.
- The Gamma function also shows up in an important relation with the Riemann zeta function, ζ(z).

- And also in the following elegant formula:
 Which is only valid for Re(z) > 1.
Which is only valid for Re(z) > 1.
- The Gamma function is intimately related to the stretched exponential function. For instance, the moments of that function are
[edit] Particular values
Main article: Particular values of the Gamma function
[edit] Approximations
Complex values of the Gamma function can be computed numerically with arbitrary precision using Stirling's approximation or the Lanczos approximation.
The Gamma function can be computed to fixed precision for ![Re(z)\in [1,2]](http://upload.wikimedia.org/math/e/f/d/efd3cf2f201cd54a69183a82ad27cdd7.png) by applying integration by parts to Euler's integral. Choose any large number x; then the Gamma function can be written
by applying integration by parts to Euler's integral. Choose any large number x; then the Gamma function can be written
and if ![Re(z)\in[1,2]](http://upload.wikimedia.org/math/e/f/d/efd3cf2f201cd54a69183a82ad27cdd7.png) then the last integral is smaller than x exp(−x) < 2−N. Thus it can be made small enough to be negligible: by choosing an appropriate x, the Gamma function can be evaluated to N bits of precision with the above series. If z is rational, the computation can be performed with binary splitting in time O( (log(N))2 M(N) ) where M(N) is the time needed to multiply two N-bit numbers.
then the last integral is smaller than x exp(−x) < 2−N. Thus it can be made small enough to be negligible: by choosing an appropriate x, the Gamma function can be evaluated to N bits of precision with the above series. If z is rational, the computation can be performed with binary splitting in time O( (log(N))2 M(N) ) where M(N) is the time needed to multiply two N-bit numbers.
For arguments that are integer multiples of 1/24 the Gamma function can also be evaluated quickly using arithmetic-geometric mean iterations (see particular values of the Gamma function).
Because the Gamma and factorial functions grow so rapidly for moderately-large arguments, many computing environments include a function that returns the natural logarithm of the Gamma function (often given the name lngamma); this grows much more slowly, and for combinatorial calculations allows adding and subtracting logs instead of multiplying and dividing very large values. The digamma function, which is the derivative of this function, is also commonly seen.
[edit] See also
- Beta function
- Bohr-Mollerup theorem
- Digamma function
- Elliptic gamma function
- Factorial
- Gamma distribution
- Gauss's constant
- Gauss sum
- Incomplete gamma function
- Lanczos approximation
- Multivariate Gamma function
- Pochhammer k-symbol
- Polygamma function
- Reciprocal Gamma function
- Stirling's approximation
- Trigamma function
[edit] Notes
- ^ George Allen, and Unwin, Ltd., The Universal Encyclopedia of Mathematics. United States of America, New American Library, Simon and Schuster, Inc., 1964. (Forward by James R. Newman)
[edit] References
- Philip J. Davis, "Leonhard Euler's Integral: A Historical Profile of the Gamma Function," Am. Math. Monthly 66, 849-869 (1959)
- Eric W. Weisstein, Gamma function at MathWorld.
- Pascal Sebah and Xavier Gourdon. Introduction to the Gamma Function. In PostScript and HTML formats.
- Bruno Haible & Thomas Papanikolaou. Fast multiprecision evaluation of series of rational numbers. Technical Report No. TI-7/97, Darmstadt University of Technology, 1997
- Julian Havil, Gamma, Exploring Euler's Constant", ISBN 0-691-09983-9 (c) 2003
- Emil Artin, "The Gamma function", in Rosen, Michael (ed.) Exposition by Emil Artin: a selection; History of Mathematics 30. Providence, RI: American Mathematical Society (2006).
[edit] External links
| Wikimedia Commons has media related to: Gamma and related functions |
[edit] Web sites
- Askey, R. A.; Roy, R. (2008), "Gamma function", in Boisvert, Ronald F.; Clark, Charles W.; Lozier, Daniel M. et al., Digital Library of Mathematical Functions, N.I.S.T.
- Cephes - C and C++ language special functions math library
- Examples of problems involving the Gamma function can be found at Exampleproblems.com.
- Gamma function calculator
- Wolfram gamma function evaluator (arbitrary precision)
- Gamma at the Wolfram Functions Site.
- Volume of n-Spheres and the Gamma Function at MathPages
- Computing the Gamma function - various algorithms
- Online tool to graph functions which contain the Gamma function
[edit] Further reading
- Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. (See Chapter 6)
- G. Arfken and H. Weber. Mathematical Methods for Physicists. Harcourt/Academic Press, 2000. (See Chapter 10.)
- Harry Hochstadt. The Functions of Mathematical Physics. New York: Dover, 1986 (See Chapter 3.)
- W.H. Press, B.P. Flannery, S.A. Teukolsky, and W.T. Vetterling. Numerical Recipes in C. Cambridge, UK: Cambridge University Press, 1988. (See Section 6.1.)





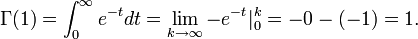



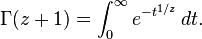












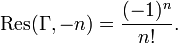

![\begin{align}
&= \left[ t^{z}\frac{1}{\log(e^{-1})}(e^{-1})^{t} \right]_{0}^{\infty} + \int_0^\infty zt^{z-1}e^{-t}\,\mathrm{d}t \\
&= \underbrace{[ -t^{z}e^{-t} ]_{0}^{\infty}}_{=0-0} + \int_0^\infty zt^{z-1}e^{-t}\,\mathrm{d}t \\
&= z\int_0^\infty t^{z-1}e^{-t}\,\mathrm{d}t \\
&= z\Gamma(z).
\end{align}](http://upload.wikimedia.org/math/c/4/6/c462f45653d8b784cfef3339afdafaeb.png)










