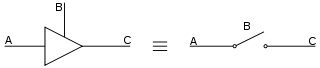Logic gate
From Wikipedia, the free encyclopedia
A logic gate performs a logical operation on one or more logic inputs and produces a single logic output. The logic normally performed is Boolean logic and is most commonly found in digital circuits. Logic gates are primarily implemented electronically using diodes or transistors, but can also be constructed using electromagnetic relays, fluidics, optics, molecules, or even mechanical elements.
In electronic logic, a logic level is represented by a voltage or current, (which depends on the type of electronic logic in use). Each logic gate requires power so that it can source and sink currents to achieve the correct output voltage. In logic circuit diagrams the power is not shown, but in a full electronic schematic, power connections are required.
Contents |
[edit] Truth table
A truth table is a table that describes the behaviour of a logic gate. It lists the value of the output for every possible combination of the inputs and can be used to simplify the number of logic gates and level of nesting in an electronic circuit. In general the truth table does not lead to an efficient implementation; a minimization procedure, using Karnaugh maps, the Quine–McCluskey algorithm or a heuristic algorithm is required for reducing the circuit complexity.
[edit] Background
The simplest form of electronic logic is diode logic. This allows AND and OR gates to be built, but not inverters, and so is an incomplete form of logic. Further, without some kind of amplification it is not possible to have such basic logic operations cascaded as required for more complex logic functions. To build a functionally complete logic system, relays, valves (vacuum tubes), or transistors can be used. The simplest family of logic gates using bipolar transistors is called resistor-transistor logic, or RTL. Unlike diode logic gates, RTL gates can be cascaded indefinitely to produce more complex logic functions. These gates were used in early integrated circuits. For higher speed, the resistors used in RTL were replaced by diodes, leading to diode-transistor logic, or DTL. It was then discovered that one transistor could do the job of two diodes in the space of one diode even better, by more quickly switching off the following stage, so transistor-transistor logic, or TTL, was created. In virtually every type of contemporary chip implementation of digital systems, the bipolar transistors have been replaced by complementary field-effect transistors (MOSFETs) to reduce size and power consumption still further, thereby resulting in complementary metal–oxide–semiconductor (CMOS) logic.
For small-scale logic, designers now use prefabricated logic gates from families of devices such as the TTL 7400 series by Texas Instruments and the CMOS 4000 series by RCA, and their more recent descendants. Increasingly, these fixed-function logic gates are being replaced by programmable logic devices, which allow designers to pack a large number of mixed logic gates into a single integrated circuit. The field-programmable nature of programmable logic devices such as FPGAs has removed the 'hard' property of hardware; it is now possible to change the logic design of a hardware system by reprogramming some of its components, thus allowing the features or function of a hardware implementation of a logic system to be changed.
Electronic logic gates differ significantly from their relay-and-switch equivalents. They are much faster, consume much less power, and are much smaller (all by a factor of a million or more in most cases). Also, there is a fundamental structural difference. The switch circuit creates a continuous metallic path for current to flow (in either direction) between its input and its output. The semiconductor logic gate, on the other hand, acts as a high-gain voltage amplifier, which sinks a tiny current at its input and produces a low-impedance voltage at its output. It is not possible for current to flow between the output and the input of a semiconductor logic gate.
Another important advantage of standardised integrated circuit logic families, such as the 7400 and 4000 families, is that they are cascadable. This means that the output of one gate can be wired to the inputs of one or several other gates, and so on. Systems of arbitrary complexity can be built without great concern of the designer for the internal workings of the gates, provided the limitations of each integrated circuit are considered.
The output of one gate can only drive a finite number of inputs to other gates, a number called the 'fanout limit'. Also, there is always a delay, called the 'propagation delay', from a change in input of a gate to the corresponding change in its output. When gates are cascaded, the total propagation delay is approximately the sum of the individual delays, an effect which can become a problem in high-speed circuits. Additional delay can be caused when a large number of inputs are connected to an output, due to the distributed capacitance of all the inputs and wiring and the finite amount of current that each output can provide.
[edit] Logic gates
NAND and NOR logic gates are the two pillars of logic, in that all other types of Boolean logic gates (i.e., AND, OR, NOT, XOR, XNOR) can be created from a suitable network of just NAND or just NOR gate(s). They can be built from relays or transistors, or any other technology that can create an inverter and a two-input AND or OR gate. Hence the NAND and NOR gates are called the universal gates.
For an input of 2 variables, there are 16 possible boolean algebraic functions. These 16 functions are enumerated below, together with their outputs for each combination of inputs variables.
| INPUT | A | 0 | 0 | 1 | 1 | Meaning | |
|---|---|---|---|---|---|---|---|
| B | 0 | 1 | 0 | 1 | |||
| OUTPUT | FALSE | 0 | 0 | 0 | 0 | Whatever A and B, the output is false. Contradiction. | |
| A AND B | 0 | 0 | 0 | 1 | Output is true if and only if (iff) both A and B are true. | ||
A  B B |
0 | 0 | 1 | 0 | A doesn't imply B. True iff A but not B. | ||
| A | 0 | 0 | 1 | 1 | True whenever A is true. | ||
A 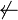 B B |
0 | 1 | 0 | 0 | A is not implied by B. True iff not A but B. | ||
| B | 0 | 1 | 0 | 1 | True whenever B is true. | ||
| A XOR B | 0 | 1 | 1 | 0 | True iff A is not equal to B. | ||
| A OR B | 0 | 1 | 1 | 1 | True iff A is true, or B is true, or both. | ||
| A NOR B | 1 | 0 | 0 | 0 | True iff neither A nor B. | ||
| A XNOR B | 1 | 0 | 0 | 1 | True iff A is equal to B. | ||
| NOT B | 1 | 0 | 1 | 0 | True iff B is false. | ||
A  B B |
1 | 0 | 1 | 1 | A is implied by B. False if not A but B, otherwise true. | ||
| NOT A | 1 | 1 | 0 | 0 | True iff A is false. | ||
A 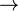 B B |
1 | 1 | 0 | 1 | A implies B. False if A but not B, otherwise true. | ||
| A NAND B | 1 | 1 | 1 | 0 | A and B are not both true. | ||
| TRUE | 1 | 1 | 1 | 1 | Whatever A and B, the output is true. Tautology. | ||
The four functions denoted by arrows are the logical implication functions. These functions are generally less common, and are usually not implemented directly as logic gates, but rather built out of gates like AND and OR.
[edit] Symbols
There are two sets of symbols in common use, both now defined by ANSI/IEEE Std 91-1984 and its supplement ANSI/IEEE Std 91a-1991. The "distinctive shape" set, based on traditional schematics, is used for simple drawings and is quicker to draw by hand. It is sometimes unofficially described as "military", reflecting its origin if not its modern usage. The "rectangular shape" set, based on IEC 60617-12, has rectangular outlines for all types of gate, and allows representation of a much wider range of devices than is possible with the traditional symbols. The IEC's system has been adopted by other standards, such as EN 60617-12:1999 in Europe and BS EN 60617-12:1999 in the United Kingdom.
The goal of IEEE Std 91-1984 was to provide a uniform method of describing the complex logic functions of digital circuits with schematic symbols. These functions were more complex than simple AND and OR gates. They could be medium scale circuits such as a 4-bit counter to a large scale circuits such as a microprocessor. The 1984 version did not include the "distinctive shape" symbols.[1] These were added to the 1991 supplement with this note: "The distinctive-shape symbol is, according to IEC Publication 617, Part 12, not preferred, but is not considered to be in contradiction to that standard."
In the 1980s, schematics were the predominant method to design both circuit boards and custom ICs known as gate arrays. Today custom ICs and the field-programmable gate array are typically designed with Hardware Description Languages (HDL) such as Verilog or VHDL. The need for complex logic symbols has diminished and distinctive shape symbols are still the predominate style.[citation needed]
| Type | Distinctive shape | Rectangular shape | Boolean algebra between A & B | Truth table | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AND | 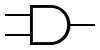 |
 |
 |
|
||||||||||||||||||
| OR | 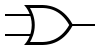 |
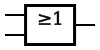 |
A + B |
|
||||||||||||||||||
| NOT | 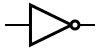 |
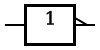 |
 |
|
||||||||||||||||||
| In electronics a NOT gate is more commonly called an inverter. The circle on the symbol is called a bubble, and is generally used in circuit diagrams to indicate an inverted (active-low) input or output.[1] | ||||||||||||||||||||||
| NAND |  |
 |
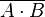 |
|
||||||||||||||||||
| NOR |  |
 |
 |
|
||||||||||||||||||
| XOR | 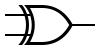 |
 |
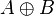 |
|
||||||||||||||||||
| XNOR | 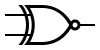 |
 |
 |
|
||||||||||||||||||
In practice, the cheapest gate to manufacture is usually the NAND gate. Additionally, Charles Peirce showed that NAND gates alone (as well as NOR gates alone) can be used to reproduce the functions of all the other logic gates.
Two more gates are the exclusive-OR or XOR function and its inverse, exclusive-NOR or XNOR. The two input Exclusive-OR is true only when the two input values are different, false if they are equal, regardless of the value. If there are more than two inputs, the gate generates a true at its output if the number of trues at its input is odd ([2]). In practice, these gates are built from combinations of simpler logic gates.
[edit] De Morgan equivalent symbols
By use of De Morgan's theorem, an AND gate can be turned into an OR gate by inverting the sense of the logic at its inputs and outputs. This leads to a separate ends can be replaced by a simple bubble-less connection and a suitable change of gate. If the NAND is drawn as OR with input bubbles, and a NOR as AND with input bubbles, this gate substitution occurs automatically in the diagram (effectively, bubbles "cancel"). This is commonly seen in real logic diagrams - thus the reader must not get into the habit of associating the shapes exclusively as OR or AND shapes, but also take into account the bubbles at both inputs and outputs in order to determine the "true" logic function indicated.
All logic relations can be realized by using NAND gates. (This can also be done using NOR gates). De Morgan's theorem is most commonly used to transform all logic gates to NAND gates or NOR gates. This is done mainly since it is easy to buy logic gates in bulk and because many electronics labs stock only NAND and NOR gates.
[edit] Storage of bits
Related to the concept of logic gates (and also built from them) is the idea of storing a bit of information. None of the gates discussed up to here can store a value by itself: when the inputs change, the outputs immediately react. It is possible to make a storage element either through a capacitor (which stores charge due to its physical properties) or by feedback. Connecting the output of a gate to the input causes it to be put through the logic again, and choosing the feedback correctly allows it to be preserved or modified through the use of other inputs. A set of gates arranged in this fashion is known as a "latch", and more complicated designs that utilize clock signals and change only on the rising edge are called edge-triggered "flip-flops". The combination of multiple flip-flops in parallel, to store a multiple-bit value, is known as a register. When using any of these gate setups the overall system has memory; it is then called a sequential logic system since its output can be influenced by its previous state(s).
These registers or capacitor-based circuits are known as computer memory. They vary in performance, based on factors of speed, complexity, and reliability of storage, and many different types of designs are used based on the application.
[edit] Three-state logic gates
Three-state, or 3-state, logic gates have three states of the output: high (H), low (L) and high-impedance (Z). The high-impedance state plays no role in the logic, which remains strictly binary. These devices are used on buses to allow multiple chips to send data. A group of three-states driving a line with a suitable control circuit is basically equivalent to a multiplexer, which may be physically distributed over separate devices or plug-in cards.
In electronics, a high output would mean the output is sourcing current from the positive power terminal (positive voltage). A low output would mean the output is sinking current to the negative power terminal (zero voltage). High impedance would mean that the output is effectively disconnected from the circuit.
'Tri-state', a widely-used synonym of 'three-state', is a trademark of the National Semiconductor Corporation.
[edit] Miscellaneous
Logic circuits include such devices as multiplexers, registers, arithmetic logic units (ALUs), and computer memory, all the way up through complete microprocessors which can contain more than a 100 million gates. In practice, the gates are made from field-effect transistors (FETs), particularly MOSFETs.
Compound logic gates AND-OR-Invert (AOI) and OR-AND-Invert (OAI) are often employed in circuit design because their construction using MOSFET's is simpler and more efficient than the sum of the individual gates.[2]
In reversible logic, Toffoli gates are used.
[edit] History and development
The earliest logic gates were made mechanically. Charles Babbage, around 1837, devised the Analytical Engine. His logic gates relied on mechanical gearing to perform operations. Electromagnetic relays were later used for logic gates. In 1891, Almon Strowger patented a device containing a logic gate switch circuit (U.S. Patent 0,447,918). Strowger's patent was not in widespread use until the 1920s. Starting in 1898, Nikola Tesla filed for patents of devices containing logic gate circuits (see List of Tesla patents). Eventually, vacuum tubes replaced relays for logic operations. Lee De Forest's modification, in 1907, of the Fleming valve can be used as AND logic gate. Ludwig Wittgenstein introduced a version of the 16-row truth table, which is shown above, as proposition 5.101 of Tractatus Logico-Philosophicus (1921). Claude E. Shannon introduced the use of Boolean algebra in the analysis and design of switching circuits in 1937. Walther Bothe, inventor of the coincidence circuit, got part of the 1954 Nobel Prize in physics, for the first modern electronic AND gate in 1924. Active research is taking place in molecular logic gates.
[edit] Implementations
As of 2008, most logic gates are made of CMOS transistors. Often millions of logic gates are packaged in a single integrated circuit.
The most common implementations of logic gates are based on electronics using resistors, transistors and diodes. There are several logic gate design paradigms based on these components. Each paradigm leads to a logic family with different advantages (efficiency, speed, cost, size, reliability...): RDL (resistor-diode logic), RTL (resistor-transistor logic), DTL (diode-transistor logic), TTL (transistor-transistor logic) and CMOS (complementary metal oxide semiconductor). It is also possible to make logic gates out of relays, a design used in certain scenarios for increased robustness.
It is also possible to create mechanical logic gates, including on a molecular scale. [3] Logic gates have been made out of DNA (see DNA nanotechnology)[4] and used to create a computer called MAYA (see MAYA II).
Additionally, logic gates can be made from quantum mechanical effects (though quantum computing usually diverges from boolean design), and non-linear optical effects.
[edit] See also
- And-inverter graph
- Boolean algebra topics
- Boolean function
- Digital circuit
- Espresso heuristic logic minimizer
- Fanout
- Flip-flop (electronics)
- Karnaugh map
- Logic family
- Logical graph
- NMOS logic
- Propositional calculus
- Race hazard
- Reversible computing
- Truth table
[edit] References
- ^ Winfield Hill and Paul Horowitz (1989). The Art of Electronics. Cambridge University Press. ISBN 0521377099. http://books.google.com/books?id=Ksa2pWfNnvkC&pg=PA322&dq=bubble+active-low&ei=9u75RqWsKoSepgKhzJi-CQ&sig=kXvQtTNPt3BRWu3DMtwLgOF-p6s.
- ^ Tinder, Richard F. (2000). Engineering digital design: Revised Second Edition. pp. 317–319. ISBN 0126912955. http://books.google.com/books?id=6x0pjjMKRh0C&pg=PT347&lpg=PT347&dq=AOI+gate&source=web&ots=t-wt6hoi1-&sig=dlnF_Kq9jYe27dbr7Rb5gThgM2Y&hl=en&sa=X&oi=book_result&resnum=7&ct=result#PPT346,M1. Retrieved on 2008-07-04.
- ^ Mechanical Logic gates (focused on molecular scale)
- ^ DNA Logic gates
- Symbols for logic gates. Twenty First Century Books, Breckenridge, CO.
- Wireless Remote Control and the Electronic Computer Logic logic elements
- "LEGO Logic Gates". goldfish.org.uk, 2005.
[edit] Further Reading
- Awschalom, D., D. Loss, and N. Samarth, Semiconductor Spintronics and Quantum Computation (2002), Springer-Verlag, Berlin, Germany.
- Bostock, Geoff, Programmable Logic Devices. Technology and Applications (1988), McGraw-Hill, New York, NY.
- Brown, Stephen D. et al., Field-Programmable Gate Arrays (1992), Kluwer Academic Publishers, Boston, MA.
[edit] External links
- Online logic gate simulator
- Java applet of NOT gate
- Digital Circuit Simulator (Online and Windows Program)
|
|||||||||||