Just intonation

From Wikipedia, the free encyclopedia

In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of whole numbers. Any interval tuned in this way is called a just interval; in other words, the two notes are members of the same harmonic series.

Justly tuned intervals are usually written either as ratios, with a colon (for example, 3:2), or as fractions, with a slash (3/2). Sometimes a technical distinction^{[clarification needed]} is made between the two styles, but in general they are equivalent and interchangeable.

Although in theory two notes tuned in an arbitrary frequency ratio such as 1024:927 might be said to be justly tuned, in practice only ratios using products of small primes are given the name; more complex ratios are often considered to be rational intonation but not necessarily just intonation. Intervals used are then capable of being more consonant.

Just intonation is usually contrasted and compared with equal temperament, the tuning system that is by far the most common in the West, which arranges all notes at multiples of the same basic interval. Equal temperament results in a tuning system where all intervals will have exactly the same character in any key but the intervals themselves are detuned slightly relative to just intonation. Each interval possesses its own degree of detuning.

[edit] Examples

Just intonation (help·info) An A-major scale, followed by three major triads, and then a progression of fifths in just intonation.

Equal temperament (help·info) An A-major scale, followed by three major triads, and then a progression of fifths in equal temperament. If you listen to the above file, and then listen to this one, you might be able to hear a slight buzzing in this file.

Equal temperament and just intonation compared (help·info) A pair of major thirds, followed by a pair of full major chords. The first in each pair is in equal temperament; the second is in just intonation. Piano sound.

Equal temperament and just intonation compared with square waveform (help·info) A pair of major chords. The first is in equal temperament; the second is in just intonation. The pair of chords is repeated with a transition from equal temperament to just temperament between the two chords. In the equal temperament chords a roughness or beating can be heard at about 4 hz and about 0.8 Hz. In the just intonation triad this roughness is absent. The square waveform makes the difference between equal and just temperaments more obvious.

[edit] History

There were several other systems in use before equal temperament. The Guqin has a musical scale based on harmonic overtone positions. The dots indicate the harmonic positions: 1/8, 1/6, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 5/6, 7/8^[1]. Pythagorean tuning, perhaps the first tuning system to be theorized in the West,^[2], is a system in which all tones can be found using the ratios 3:2 . It is easier to think of this system as a cycle of fifths, but it must be noted that because a series of 12 fifths does not reach the same tone it began with, this system produces wolf fifths in the more distant keys (which were consequently unused).

Another system that was popular for keyboards through the Renaissance was meantone temperament^[3]. In this system the simpler ratios of 3:2 and 4:3 were compromised in favour of exact 5:4 (major thirds) ratios. Specifically, the fifth (3:2) was slightly narrowed so that a series of four narrowed fifths would produce 5:4 exactly (at some octave transposition). Again, this system is not circular and produced some unplayable keys. (Some keyboards of the 18th century featured split keys differentiating sharp and flat notes to expand the range of usable keys.)

The most common tuning today began as well temperament, which was replaced by the more rigorous equal temperament in the early 20th century.^{[citation needed]} Well temperament largely abandoned just intonation by applying small changes to the intervals so that they became more homogenized and eliminated wolf intervals. In systems of well temperament, and there were many, the goal was to make all keys usable by compromising each of them slightly. Its development was necessary as composers moved toward expression through large harmonic changes (modulation), and required access to a wider realm of tonality. Bach's "Well-Tempered Clavier", a book of compositions in every key, is the most famous example, but the compositions of Chopin, for instance, rely much more on the devices of expression only allowed by well temperament^[4].

Equal temperament is essentially the most homogenized form of well temperament, in that it tunes an actual circle of fifths by narrowing each by the same amount. In equal temperament, every interval is the same as all other intervals of its type. There are no longer pure and "wolf" fifths, or even good and bad fifths, but simply fifths (or thirds, or seconds, et cetera). Equal temperament is not a form of just intonation.

Today, the dominance of repertoire composed under well tempered systems, the prominence of the piano in musical training, the lack of just-intonation capable instruments, and the fact that tuning is not normally a significant part of a musician's education have made equal temperament sufficiently more prevalent that alternatives are not often discussed.

Despite the obstacles, many today find reasons to pursue just intonation. The purity and stability of its intervals are found quite beautiful by many, but this stability also allows extreme intonational precision as well. The practical study of just intonation can greatly increase one's analytical ability with respect to sound, and yield improvement to musicianship even in well temperament repertoire.^{[citation needed]}

In practice it is very difficult to produce true equal temperament.^{[citation needed]} There are instruments such as the piano where tuning is not dependent on the performer, but these instruments are a minority. The main problem with equal temperament is that its intervals must sound somewhat unstable, and thus the performer has to learn to suppress the more stable just intervals in favour of equal tempered ones. This is counterintuitive, and in small groups, notably string quartets, just intonation is often approached either by accident or design because it is much easier to find (and hear) a point of stability than a point of arbitrary instability.^{[citation needed]}

In modern pop music the equal temperament is most commonly used. When the sound of an instrument is enhanced by overdriving the amplifier however the natural overtones increase in volume and interfere with the fundamental tones of the 'out of tune' strings. This is the reason why the sound of heavily driven guitars becomes muddy and unclear. The word distortion is a bit poorly chosen, because it enhances the natural overtones instead of 'distorting' the sound. It is distorting the chords in fact.

[edit] Diatonic scale

It is possible to tune the familiar diatonic scale or chromatic scale in just intonation in many ways, all of which make certain chords purely tuned and as consonant and stable as possible, and the other chords not accommodated sound considerably less stable.

The prominent notes of a given scale are tuned so that their frequencies form ratios of relatively small integers. For example, in the key of G major, the ratio of the frequencies of the notes G to D (a perfect fifth) is 3/2, while that of G to C (a perfect fourth) is 4/3. Three basic intervals can be used to construct any interval involving the prime numbers 2, 3, and 5 (known as 5-limit just intonation):

s = 16:15 (Semitone)
t = 10:9 (Minor tone)
T = 9:8 (Major tone)

which combine to form:

6:5 = Ts (minor third)
5:4 = Tt (major third)
4:3 = Tts (perfect fourth)
3:2 = TTts (perfect fifth)
2:1 = TTTttss (octave)

A just diatonic scale may be derived as follows. Suppose we insist that the chords F-A-C, C-E-G, and G-B-D be just major triads (then A-C-E and E-G-B are just minor triads, but D-F-A is not).

Then we obtain this scale:

Note	C		D		E		F		G		A		B		C
Ratio	1/1		9/8		5/4		4/3		3/2		5/3		15/8		2/1
Cents	0.00		203.91		386.31		498.04		701.96		884.36		1088.27		1200.00
Step		T		t		s		T		t		T		s
Cent step		203.91		182.40		111.73		203.91		182.40		203.91		111.73

The major thirds are correct, and two minor thirds are right, but D-F is not.

Another way to do it is as follows. We can insist that the chords D-F-A, A-C-E, and E-G-B be just minor triads (then F-A-C and C-E-G are just major triads, but G-B-D is not).

Then we get the following scale:

Note	A		B		C		D		E		F		G		A
Ratio	1/1		9/8		6/5		4/3		3/2		8/5		9/5		2/1
Cents	0.00		203.91		315.64		498.04		701.96		813.69		1017.60		1200.00
Step		T		s		t		T		s		T		t
Cent step		203.91		111.73		182.40		203.91		111.73		203.91		182.40

The major thirds are correct, and two minor thirds are right, but B-D is not.

If we compare with the scale above, we see that six notes can be lined up, but one note, D, has changed its value. It is evidently not possible to get all six chords mentioned correct.

There are other possibilities; instead of lowering D, we can raise A. But this breaks something else.

[edit] Twelve tone scale

There are several ways to create a just tuning of the twelve tone scale.

The oldest known form of tuning, Pythagorean tuning, can produce a twelve tone scale, but it does so by involving ratios of very large numbers, corresponding to natural harmonics very high in the harmonic series that do not occur widely in physical phenomena. This tuning uses ratios involving only powers of 3 and 2, creating a cycle of just perfect fifths, as follows:

Note	G♭	D♭	A♭	E♭	B♭	F	C	G	D	A	E	B	F♯
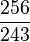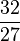Ratio	$\frac{1024}{729}$	$\frac{256}{243}$	$\frac{128}{81}$	$\frac{32}{27}$	$\frac{16}{9}$	$\frac{4}{3}$	$\frac{1}{1}$	$\frac{3}{2}$	$\frac{9}{8}$	$\frac{27}{16}$	$\frac{81}{64}$	$\frac{243}{128}$	$\frac{729}{512}$
Cents	588.27	90.22	792.18	294.13	996.09	498.04	0.00	701.96	203.91	905.87	407.82	1109.78	611.73

Between enharmonic notes at either end of the cycle is a difference of about 24 cents, known as the Pythagorean comma. This twelve tone scale is fairly close to Equal temperament, but it does not offer much advantage for tonal harmony because only the perfect intervals (fourth, fifth, and octave) are simple enough to sound pure. Major thirds, for instance, receive the rather unstable interval of 81/64, sharp (by the ratio of 81:80) ^[5] of the preferred 5/4. The primary reason for its use is that it is extremely easy to tune, as its building block, the perfect fifth, is the simplest interval after the octave and unison.

A twelve tone scale can also be created with intervals that are compounded second third and fifth harmonics, called a five-limit tuning. Only factors 2, 3 and 5 are used in the construction summarized in the table below:

Factor	1/(3*3)	1/3	1	3	3*3
5		5/3 A: 5/3	5 E: 5/4	15 B: 15/8	45 F♯: 45/32
1	1/9 B♭: 16/9	1/3 F: 4/3	1 C: 1	3 G: 3/2	9 D: 9/8
1/5	1/45 G♭: 64/45	1/15 D♭: 16/15	1/5 A♭: 8/5	3/5 E♭: 6/5

Starting with C in the centre of this diagram, horizontally a relationship by 3 is applied and vertically by 5. To all fractions outside the range of 1 to 2, powers of 2 are used to bring the tones within the same octave. Between the ends of the chain, F♯ and G♭, the enharmonic comma is less than 20 cents. This system has the advantage of making available pure thirds (5/4 and 6/5) as well as fifths, but also contains many intervals that are not (e.g. D to A is 40/27 rather than 3/2, or B♭ to D is the Pythagorean 81/64 rather than 5/4) which practically limits modulation to a narrow range of keys.

[edit] Indian scales

In Indian music, the just diatonic scale described above is used, though there are different possibilities for the 6th pitch (Dha), and further modifications may be made to all pitches excepting Sa and Pa.^[6]

Note	Sa	Re	Ga	Ma	Pa	Dha	Ni	Sa
Ratio	1/1	9/8	5/4	4/3	3/2	5/3 or 27/16	15/8	2/1
Cents	0.00	203.91	386.31	498.04	701.96	884.36 or 905.87	1088.27	1200.00

Both possible scales appear problematic, if one were to look at it in terms of a polyphonic application. The first would have a problem because (27/16)/(5/4) = 27/20, which is a wolf interval, being uncomfortably close to the purer 4:3. However, because Indian music uses melodies over a drone dyad^[7] (usually 1/1 and 3/2), these two pitches (27/16 and 5/4) would not be heard sounding together. See Swara and Śruti (music).

The alternative, using 5/3 for Dha gives (5/3)/(5/4) = 4/3, and allows these notes to sound together in a consonant fashion, but then introduces another problem as (5/3)/(9/8) = 40/27, which is another wolf interval, this time close to 3/2. These wolf intervals are incompatible with much western music, but in Indian music they are irrelevant.

Some accounts of Indian intonation system cite a given 22 Śrutis. According to some musicians, you have a scale of a given 12 pitches and ten in addition (the tonic, Shadja (Sa), and the pure fifth, Pancham (Pa), are inviolate):

Note	C	D♭	D♭	D	D	E♭	E♭	E	E	F	F	F♯
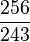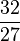Ratio	$\frac{1}{1}$	$\frac{256}{243}$	$\frac{16}{15}$	$\frac{10}{9}$	$\frac{9}{8}$	$\frac{32}{27}$	$\frac{6}{5}$	$\frac{5}{4}$	$\frac{81}{64}$	$\frac{27}{20}$	$\frac{4}{3}$	$\frac{45}{32}$
Cents	0.00	90.22	111.73	182.40	203.91	294.13	315.64	386.31	407.82	519.55	498.04	590.22

Note	F♯	G	A♭	A♭	A	A	B♭	B♭	B	B	C
Ratio	$\frac{64}{45}$	$\frac{3}{2}$	$\frac{128}{81}$	$\frac{8}{5}$	$\frac{5}{3}$	$\frac{27}{16}$	$\frac{16}{9}$	$\frac{9}{5}$	$\frac{15}{8}$	$\frac{243}{128}$	$\frac{2}{1}$
Cents	609.78	701.96	792.18	813.69	884.36	905.87	996.09	1017.60	1088.27	1109.78	1200.00

Where we have two ratios for a given letter name, we have a difference of 81:80, which is known as the syntonic comma.^[8] You can see the symmetry, looking at it from the tonic, then the octave.

(This is just one example of "explaining" a 22-Śruti scale of tones. There are many takes on this, just as there are many ears.)

[edit] Practical difficulties

Some fixed just intonation scales and systems, such as the diatonic scale above, produce wolf intervals. The above scale allows a minor tone to occur next to a semitone which produces the awkward ratio 32:27 for F:D, and still worse, a minor tone next to a fourth giving 40:27 for A:D. Moving D down to 10/9 alleviates these difficulties but creates new ones: G:D becomes 27:20, and B:G becomes 27:16.

You can have more frets on a guitar to handle both A's, 9/8 with respect to G and 10/9 with respect to G so that C:A can be played as 6:5 while D:A can still be played as 3:2. 9/8 and 10/9 are less than 1/53 octave apart, so mechanical and performance considerations have made this approach extremely rare. And the problem of how to tune chords such as C-E-G-A-D is left unresolved (for instance, A could be 4:3 below D (making it 9/8, if G is 1) or 4:3 above E (making it 10/9, if G is 1) but not both at the same time, so one of the fourths in the chord will have to be an out-of-tune wolf interval). However the frets may be removed entirely—this, unfortunately, makes in-tune fingering of many chords exceedingly difficult, due to the construction and mechanics of the human hand—and the tuning of most complex chords in just intonation is generally ambiguous.

For many instruments tuned in just intonation, you can't change keys without retuning your instrument. For instance, if you tune a piano to just intonation intervals and a minimum of wolf intervals for the key of G, then only one other key (typically E-flat) can have the same intervals, and many of the keys have a very dissonant and unpleasant sound. This makes modulation within a piece, or playing a repertoire of pieces in different keys, impractical to impossible.

Synthesizers have proven a valuable tool for composers wanting to experiment with just intonation. Many commercial synthesizers provide the ability to use built-in just intonation scales or to program your own. Wendy Carlos used a system on her 1986 album Beauty in the Beast, where one electronic keyboard was used to play the notes, and another used to instantly set the root note to which all intervals were tuned, which allowed for modulation. On her 1987 lecture album Secrets of Synthesis there are audible examples of the difference in sound between equal temperament and just intonation.

[edit] Singing

The human voice is among the most pitch-flexible instruments in common use. Pitch can be varied with no restraints and adjusted in the midst of performance, without needing to retune (as even with the otherwise flexible string instruments). Although the explicit use of just intonation fell out of favour concurrently with the increasing use of instrumental accompaniment (with its attendant constraints on pitch), most a cappella ensembles naturally tend toward just intonation because of the comfort of its stability.^{[citation needed]} Barbershop quartets are a good example of this.

Two exemplary contemporary ensembles that meticulously tune their singing in accordance with just intonation (whenever indicated) are The Hilliard Ensemble and Orlando Consort.

[edit] Western composers

Most composers don't specify how instruments are to be tuned, although historically most have assumed one tuning system which was common in their time; in the 20th century most composers assumed equal temperament would be used. However, a few have specified just intonation systems for some or all of their compositions, including John Adams, David Beardsley, Glenn Branca, Martin Bresnick, Wendy Carlos, Lawrence Chandler, Tony Conrad, Stuart Dempster, Arnold Dreyblatt, Kyle Gann, Kraig Grady, Lou Harrison, Ben Johnston, Elodie Lauten, György Ligeti, Douglas Leedy, Pauline Oliveros, Harry Partch, Robert Rich, Terry Riley, Adam Silverman, James Tenney, Ernesto Rodrigues, Daniel James Wolf, and La Monte Young. Eivind Groven is often considered a just intonation composer but just intonation purists will disagree. His tuning system was in fact schismatic temperament, which is indeed capable of far closer approximations to just intonation consonances than 12-note equal temperament or even meantone temperament, but still alters the pure ratios of just intonation slightly in order to achieve a simpler and more flexible system than true just intonation.

Music written in just intonation is most often tonal but need not be; some music of Kraig Grady and Daniel James Wolf uses just intonation scales designed by Erv Wilson explicitly for a consonant form of atonality, and Ben Johnston's Sonata for Microtonal Piano (1964) uses serialism to achieve an atonal result. Composers often impose a limit on how complex the ratios used are: for example, a composer may write in "7-limit JI", meaning that no prime number larger than 7 features in the ratios they use. Under this scheme, the ratio 10/7, for example, would be permitted, but 11/7 would not be, as all non-prime numbers are octaves of, or mathematically and tonally related to, lower primes (example: 12 is a double octave of 3, while 9 is a square of 3). Yuri Landman derived a just intoned musical scale from a initially considered atonal prepared guitar playing technique based on adding a third bridge under the strings. When this bridge is positioned in the noded positions of the harmonic series the volume of the instrument increases and the overtone becomes clear and has a consonant relation to the complementary opposed string part creating a harmonic multiphonic tone^[9].

[edit] See also

[edit] References

^ The harmonic scale of Guqin clarified in the essay 3rd Bridge Helix by Yuri Landman on furious.com
^ The oldest known description of the Pythagorean tuning system appears in Babylonian artifacts dating to roughly . See: West, M.L.. The Babylonian Musical Notation and the Hurrian Melodic Texts, Music & Letters vol. 75 no. 2 (May 1994). pp. 161-179.
^ Grout, Donald Jay and Claude Palisca. A History of Western Music, sixth edition. W.W. Norton & Company Inc., New York, 2000. p. 349. ISBN 0-393-97527-4
^ Chopin would also write a set of compositions in every key, his 24 Preludes, which in contrast to Bach's Well-Tempered Clavier, made extensive use of the chromatic modulations characteristic of Romantic music. See: Ibid. p. 579.
^ Danielou, Alain (1968). The Ragas of Northern Indian Music. Barrie & Rockliff, London. ISBN 0214156893.
^ Bagchee, Sandeep. Nad: Understanding Raga Music. BPI (India) PVT Ltd. pp. 23. ISBN 81-86982-07-8.
^ Bagchee, Sandeep. Nad: Understanding Raga Music. BPI (India) PVT Ltd. pp. 16. ISBN 81-86982-07-8.
^ Danielou, Alain (1968). The Ragas of Northern Indian Music. Barrie & Rockliff, London. ISBN 0214156893.
^ 3rd Bridge Helix by Yuri Landman on furious.com

[edit] External links

Art of the States: microtonal/just intonation works using just intonation by American composers
The Chrysalis Foundation -- Just Intonation: Two Definitions
Dante Rosati's 21 Tone Just Intonation guitar
Just Intonation by Mark Nowitzky
Just Intonation Explained by Kyle Gann
Just Intonation Network
A selection of Just Intonation works edited by the Just Intonation Network web published on the Tellus Audio Cassette Magazine project archive at Ubuweb
Medieval Music and Arts Foundation
Music Novatory - Just Intonation
Why does Just Intonation sound so good?
Why does our musical scale have twelve notes?
The Wilson Archives
Barbieri, Patrizio. Enharmonic instruments and music, 1470-1900. (2008) Latina, Il Levante Libreria Editrice

[0] The harmonic scale of Guqin clarified in the essay 3rd Bridge Helix by Yuri Landman on furious.com

[1] The oldest known description of the Pythagorean tuning system appears in Babylonian artifacts dating to roughly . See: West, M.L.. The Babylonian Musical Notation and the Hurrian Melodic Texts, Music & Letters vol. 75 no. 2 (May 1994). pp. 161-179.

[2] Grout, Donald Jay and Claude Palisca. A History of Western Music, sixth edition. W.W. Norton & Company Inc., New York, 2000. p. 349. ISBN 0-393-97527-4

[3] Chopin would also write a set of compositions in every key, his 24 Preludes, which in contrast to Bach's Well-Tempered Clavier, made extensive use of the chromatic modulations characteristic of Romantic music. See: Ibid. p. 579.

[4] Danielou, Alain (1968). The Ragas of Northern Indian Music. Barrie & Rockliff, London. ISBN 0214156893.

[5] Bagchee, Sandeep. Nad: Understanding Raga Music. BPI (India) PVT Ltd. pp. 23. ISBN 81-86982-07-8.

[6] Bagchee, Sandeep. Nad: Understanding Raga Music. BPI (India) PVT Ltd. pp. 16. ISBN 81-86982-07-8.

[7] Danielou, Alain (1968). The Ragas of Northern Indian Music. Barrie & Rockliff, London. ISBN 0214156893.

[8] 3rd Bridge Helix by Yuri Landman on furious.com

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

Just intonation

From Wikipedia, the free encyclopedia

Contents

[edit] Examples

[edit] History

[edit] Diatonic scale

[edit] Twelve tone scale

[edit] Indian scales

[edit] Practical difficulties

[edit] Singing

[edit] Western composers

[edit] See also

[edit] References

[edit] External links

Views

Personal tools

Navigation

Search

Interaction

Toolbox

Languages