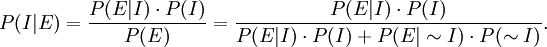Prosecutor's fallacy

From Wikipedia, the free encyclopedia

Jump to: navigation, search
 This article includes a list of references or external links, but its sources remain unclear because it has insufficient inline citations. Please help to improve this article by introducing more precise citations where appropriate. (November 2008)

The prosecutor's fallacy is any of several fallacies of statistical reasoning often used in legal arguments. Two of the most common errors are described below:

  • One form of the fallacy results from misunderstanding conditional probability, or neglecting the prior odds of a defendant being guilty; i.e., the chance an individual might be guilty even though there's no evidence directly implicating him/her. When a prosecutor has collected some evidence (for instance a DNA match) and has an expert testify that the probability of finding this evidence if the accused were innocent is tiny, the fallacy occurs if it is concluded that the probability of the accused being innocent must be comparably tiny. The probability of innocence would only be the same small value if the prior odds of guilt were exactly 1:1. In reality the probability of guilt would depend on other circumstances. If the person is already suspected for other reasons, then the probability of guilt would be very high, whereas if he is otherwise totally unconnected to the case, then we should consider a much lower prior probability of guilt, such as the overall rate of offenders in the populace for the crime in question, and the probability of guilt would be much lower.
  • Another form of the fallacy results from misunderstanding the idea of multiple testing, such as when evidence is compared against a large database. The size of the database elevates the likelihood of finding a match by pure chance alone; i.e., DNA evidence is soundest when a match is found after a single directed comparison because the existence of matches against a large database where the test sample is of poor quality (common for recovered evidence) is very likely by mere chance.

The terms "prosecutor's fallacy" and "defense attorney's fallacy" were originated by William C. Thompson and Edward Schumann in their classic article Interpretation of Statistical Evidence in Criminal Trials: The Prosecutor's Fallacy and the Defense Attorney's Fallacy (1987).

Contents

[edit] Examples of prosecutor's fallacies

Concrete examples are helpful to understanding the statistical reasoning behind these ideas:

1. Conditional Probability. Consider this case: you win the lottery jackpot. You are then charged with having cheated, for instance with having bribed lottery officials. At the trial, the prosecutor points out that winning the lottery without cheating is extremely unlikely, and that therefore your being innocent must be comparably unlikely. This reasoning is intuitively faulty — it could be applied to any lottery winner, even though we know somebody wins the lottery nearly every week. The flaw in the logic is that the prosecutor has failed to take account of the low prior probability that you and not somebody else would win the lottery in the first place. One example of this fallacy which was once routinely used in Britain among child care agencies and law enforcement[1] was Meadow's law, which led to a number of highly publicised cases of wrongful conviction for murder. The law claimed that in child cot death (SIDS) "One is a tragedy, two is suspicious and three is murder unless there is proof to the contrary."

2. Multiple Testing In another scenario, assume a rape has been committed and that a sample is compared against 20,000 men who have their DNA on record in a database. A match is found, that man is accused and at his trial, it is testified that the probability that two DNA profiles match by chance is only 1 in 10,000. This does not mean the probability that the suspect is innocent is 1 in 10,000. Since 20,000 men were tested, there were 20,000 opportunities to find a match by chance; the probability that there was at least one DNA match is

1 - \left(1-\frac{1}{10000}\right)^{20000} \approx 86\%

which is considerably more than 1 in 10,000. (The probability that exactly one of the 20,000 men has a match is about 27%, which is still rather high.)

The results above were obtained using the General Equation for Binomial probability which is:

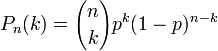
P_n(k)={n \choose k}p^k(1- p)^{n-k}

For this example, p is the probability of a DNA match by chance, n is the number of trials, and k is the number of matches by chance that are desired. Therefore, p = 0.0001, n = 20000, and k is at least 1. Because k is at least one, the answer is the sum of the General Equations from k = 1 to k = 20000. However, an easier way to solve this is to set k = 0 and subtract the result from 1:

1-\left[{20000 \choose 0}0.0001^0(1- .0001)^{20000-0}\right]

This expression reduces to about 0.8647 or about 86%.

To find the probability of exactly one DNA match by chance, simply set k = 1:

{20000 \choose 1}0.0001^1(1- .0001)^{20000-1}

This expression reduces to about 0.2707 or about 27%.

[edit] Mathematical analysis

Finding a person innocent or guilty can be viewed in mathematical terms as a form of binary classification.

A thought experiment can clarify this. A big bowl is filled with a large but unknown number of balls. Some of the balls are made of wood, and some of them are made of plastic. Of the wooden balls, 100% are white; out of the plastic balls, 99% are red and only 1% are white. A ball is pulled out at random, and observed to be white. Can the probability that the ball is wooden be calculated from the information given?

The answer is no: without knowledge of the relative proportions of wooden and plastic balls, we cannot tell how likely it is that the ball is wooden. If the number of plastic balls is far larger than the number of wooden balls, for instance, then a white ball pulled from the bowl at random is far more likely to be a white plastic ball than a white wooden ball — even though white plastic balls are a minority of the whole set of plastic balls.

The significance of this thought experiment can be seen when we substitute "guilty" and "innocent" for "wooden" and "plastic", respectively, and substitute "evidence is observed" for "white". If we observe a particular type of evidence (for instance, a suspect sharing a rare blood type with a sample that was left at a crime scene) we may think that, on that information alone, we can judge the suspect as very probably guilty. But if the number of innocent people is far larger than the number of guilty people, then the number of innocent people in whom the evidence is nevertheless observed (i.e., people who share that same rare blood type but were not involved with the crime) may also be substantially larger than the number of people of whom the evidence is observed and are guilty.

The fallacy can be analyzed using conditional probability: Suppose E is the observed evidence, and I stands for "accused is innocent". We know that P(E|I) (the probability that the evidence would be observed if the accused were innocent) is tiny. The prosecutor wrongly concludes that P(I|E) (the probability that the accused is innocent, given the evidence E) is comparatively tiny. However, P(E|I) and P(I|E) are quite different; using Bayes' theorem we see

P(I|E) = \frac{P(E|I) \cdot P(I) }{P(E)} = \frac{P(E|I) \cdot P(I) }{P(E|I) \cdot P(I) + P(E|\sim I) \cdot P(\sim I)} .

So the prior probability of innocence P(I) and the overall probability of the observed evidence P(E) need to be taken into account. Note that P(E) is the probability that evidence is observed regardless of innocence; in the third expression, it is expressed in the denominator as the sum of the probability that the person is innocent but the evidence is against him (P(E|I) times P(I)) and the probability that the person is guilty and that the evidence is against him (P(E|I bar) times P(I bar)). If P(I) is much larger than P(E), then P(I|E) can be large as well.

We can also formulate Bayes' theorem with odds:

\operatorname{Odds}(I|E) = \operatorname{Odds}(I)\cdot\frac{P(E|I)}{P(E|\sim I)}.

Without knowledge of the prior odds of I, the small value of P(E|I) does not necessarily imply that Odds(I|E) is small. (P(E|~I), the probability that the evidence is observed given the accused is guilty, is assumed to be high.)

The fallacy lies in the fact that the prior probability of guilt is not taken into account. If this probability is small, then the effect of the presented evidence is to increase that probability dramatically (by a factor of P(E|I) /P(E|~I)), but does not necessarily make it overwhelming. (In the example below of a city with 10 million people, the presented evidence raises the prior probability of guilt of 1 in 10 million to a posterior probability of guilt of 1 in 10.)

The prosecutor's fallacy is therefore no fallacy if the prior odds of guilt are assumed to be 1:1 or higher. The prior odds in fact depend on the circumstances. Was the person a suspect before the new evidence or not?

In this picture then, the fallacy consists in the fact that the prosecutor claims an absolutely low probability of innocence, without mentioning that the information he conveniently omitted would have led to a different estimate. If the person is suspected solely on the basis of this piece of evidence, then a more reasonable value for the prior odds of guilt might be a value estimated from the overall frequency of the given crime in the general population.

Deliberate and deceptive use of the prosecutor's fallacy is prosecutorial misconduct and can subject the prosecutor to official reprimand, disbarment or criminal punishment. [2]

[edit] Defendant's fallacy

Suppose there is a one-in-a-million chance of a match given that the accused is innocent. The prosecutor says this means there is only a one-in-a-million chance of innocence. But if everyone in a community of 10 million people is tested, one expects 10 matches even if everyone tested is innocent.

The defendant's fallacy would be to say, "We would expect 10 matches in this city of 10 million people, so this particular piece of evidence suggests there is a 90% chance that the accused is innocent. So this evidence cannot be used to point to a conclusion of guilt, and should be excluded."

The problem with the defendant's argument is that there may be other available evidence which on its own is also not conclusive. For example if CCTV cameras surrounding the scene of the crime spotted one hundred people there at the relevant time, one of which was the accused, then the defendant could claim: "The video suggests a 99% chance that the defendant is innocent. The match suggested a 90% chance of innocence. So the conclusion should be a finding of innocence."

When the photographic evidence is combined with the match, the two together point strongly towards guilt, since (assuming the chances of being in the photograph and having the match are independent for an innocent person) the chance that the accused is innocent is about 0.0001. Although this is not conclusive proof and only establishes low probability of innocence in a simplified model excluding other potential explanations such as a person being framed, it provides a much more compelling argument than either piece of evidence alone.

The argument goes that the prior probability that the man is innocent is 9,999,999/10,000,000. While the likelihood of having the match and being in the video may be 1 if guilty, the likelihood of the match if innocent is 1/1,000,000, and the likelihood of being in the video if innocent is 1/100,000, so (assuming independence) the likelihood of both happening if innocent is 1/100,000,000,000. That gives a posterior probability of being innocent of 9,999,999/100,009,999,999 which is 0.000099989991... or about 0.01%.

A version of this fallacy arose in the context of the OJ Simpson murder trial where the defence was prepared to argue that as only a small fraction of men who abuse their wives go on to kill them, evidence that Simpson had beaten his wife was of little consequence. The correct reasoning was to observe that a far smaller fraction of men who don't beat their wives go on to kill them.

[edit] The Sally Clark case

An example of this concept is the case of Sally Clark, a British woman who was accused in 1998 of having killed her first child at 11 weeks of age, then conceived another child and allegedly killed it at 8 weeks of age. The prosecution had expert witness Sir Roy Meadow testify that the probability of two children in the same family dying from SIDS is about 1 in 73 million. His error was to treat the two events (unexplained deaths) as statistically independent of each other. However, there is good reason to suppose that the likelihood of a death from SIDS in a family is significantly greater if a previous child has already died in these circumstances. It is also possible that some families have a greater likelihood of suffering SIDS in the first place, as a result of genetic factors not currently understood. Thus, the likelihood of two SIDS deaths in the same family cannot be computed by simply squaring the likelihood of a single such death in all families.

In the event, none of the expert witnesses in the trial suggested that SIDS was the cause of the deaths of the Clark children, and so Sir Roy's estimate could be said to be irrelevant to Sally Clark's conviction, and this was the reason that her first appeal was rejected.

Mrs Clark was convicted in 1999, resulting in a press release by the Royal Statistical Society which pointed out the mistake.[3]

A higher court later quashed Sally Clark's conviction, on other grounds, on 29 January 2003. However, Sally Clark never recovered from the court case and later died from alcohol abuse.[4]

[edit] See also

[edit] References

  1. ^ Gene find casts doubt on double 'cot death' murders. The Observer; July 15, 2001
  2. ^ http://www.abanet.org/crimjust/standards/pfunc_blk.html
  3. ^ Press release by the Royal Statistical Society about the Sally Clark case, 23 October 2001
  4. ^ "Sally Clark, mother wrongly convicted of killing her sons, found dead at home". The Guardian. March 17 2007. http://www.guardian.co.uk/society/2007/mar/17/childrensservices.uknews. Retrieved on 2008-09-25. 

[edit] External links

Retrieved from "http://en.wikipedia.org/wiki/Prosecutor%27s_fallacy"
Personal tools
Languages