Mathematical proof

From Wikipedia, the free encyclopedia

In mathematics, a proof is a convincing demonstration (within the accepted standards of the field) that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single exception. An unproved proposition that is believed to be true is known as a conjecture.

The statement that is proved is often called a theorem. Once a theorem is proved, it can be used as the basis to prove further statements. A theorem may also be referred to as a lemma, especially if it is intended for use as a stepping stone in the proof of another theorem.

Proofs employ logic but usually include some amount of natural language which usually admits some ambiguity. In fact, the vast majority of proofs in written mathematics can be considered as applications of rigorous informal logic. Purely formal proofs, written in symbolic language instead of natural language, are considered in proof theory. The distinction between formal and informal proofs has led to much examination of current and historical mathematical practice, quasi-empiricism in mathematics, and so-called folk mathematics (in both senses of that term). The philosophy of mathematics is concerned with the role of language and logic in proofs, and mathematics as a language.

[edit] History and etymology

For more details on this topic, see History of logic.

Plausibility arguments using heuristic devices such as pictures and analogies preceded strict mathematical proof..^[1] The early history of the concept of proof dates back to the early Greek and Chinese civilisations. Thales (640–546 BCE) proved some theorems in geometry. Eudoxus (408–355 BCE) and Theaetetus (417–369 BCE) formulated theorems but did not prove them. Aristotle (384–322 BCE) said definitions should describe the concept being defined in terms of other concepts already known. Euclid (300 BCE) began with undefined terms and axioms (propositions regarding the undefined terms assumed to be self-evidently true, from the Greek “axios” meaning “something worthy”) and used these to prove theorems using deductive logic. Modern proof theory treats proofs as inductively defined data structures. There is no longer an assumption that axioms are "true" in any sense; this allows for parallel mathematical theories built on alternate sets of axioms (see Axiomatic set theory and Non-Euclidean geometry for examples).

The word Proof comes from the Latin probare meaning "to test". Related modern words are the English "probe", "proboscis”, "probation", and "probability", and the Spanish "probar" (to smell or taste, or (lesser use) touch or test). The early use of "probity" was in the presentation of legal evidence. A person of authority, such as a nobleman, was said to have probity, whereby the evidence was by his relative authority, which outweighed empirical testimony.^[2]

[edit] Nature and purpose

There are two different conceptions of mathematical proof.^[3] The first is an informal proof, a rigorous natural-language expression that is intended to convince the audience of the truth of a theorem. Because of their use of natural language, the standards of rigor for informal proofs will depend on the audience of the proof. In order to be considered a proof, however, the argument must be rigorous enough; a vague or incomplete argument is not a proof. Informal proofs are the type of proof typically encountered in published mathematics. They are sometimes called "formal proofs" because of their rigor, but logicians use the term "formal proof" to refer to a different type of proof entirely.

In logic, a formal proof is not written in a natural language, but instead uses a formal language consisting of certain strings of symbols from a fixed alphabet. This allows the definition of a formal proof to be precisely specified without any ambiguity. The field of proof theory studies formal proofs and their properties. Although each informal proof can, in theory, be converted into a formal proof, this is rarely done in practice. The study of formal proofs is used to determine properties of provability in general, and to show that certain undecidable statements are not provable.

A classic question in philosophy asks whether mathematical proofs are analytic or synthetic. Kant, who introduced the analytic-synthetic distinction, believed mathematical proofs are synthetic.

Proofs may be viewed as aesthetic objects, admired for their mathematical beauty. The mathematician Paul Erdős was known for describing proofs he found particularly elegant as coming from "The Book", a hypothetical tome containing the most beautiful method(s) of proving each theorem. The book Proofs from THE BOOK, published in 2003, is devoted to presenting 32 proofs its editors find particularly pleasing.

[edit] Methods of proof

[edit] Direct proof

Main article: Direct proof

In direct proof, the conclusion is established by logically combining the axioms, definitions, and earlier theorems. For example, direct proof can be used to establish that the sum of two even integers is always even:

For any two even integers

x

and

y

we can write

x = 2 a

and

y = 2 b

for some integers

a

and

b

, since both

x

and

y

are multiples of 2. But the sum

x + y = 2 a + 2 b = 2(a + b)

is also a multiple of 2, so it is therefore even by definition.

This proof uses definition of even integers, as well as distribution law.

[edit] Proof by mathematical induction

Main article: Mathematical induction

In proof by mathematical induction, first a "base case" is proved, and then an "induction rule" is used to prove a (often infinite) series of other cases. Since the base case is true, the infinity of other cases must also be true, even if all of them cannot be proved directly because of their infinite number. A subset of induction is infinite descent. Infinite descent can be used to prove the irrationality of the square root of two.

The principle of mathematical induction states that: Let N = { 1, 2, 3, 4, ... } be the set of natural numbers and P(n) be a mathematical statement involving the natural number n belonging to N such that

(i) P(1) is true, i.e., P(n) is true for n = 1
(ii) P(n + 1) is true whenever P(n) is true, i.e., P(n) is true implies that P(n + 1) is true.

Then P(n) is true for all natural numbers n.

Mathematicians often use the term "proof by induction" as shorthand for a proof by mathematical induction.^[4] However, the term "proof by induction" may also be used in logic to mean an argument that uses inductive reasoning.

[edit] Proof by transposition

Main article: Transposition (logic)

Proof by transposition establishes the conclusion "if p then q" by proving the equivalent contrapositive statement "if not q then not p".

[edit] Proof by contradiction

Main article: Reductio ad absurdum

In proof by contradiction (also known as reductio ad absurdum, Latin for "by reduction toward the absurd"), it is shown that if some statement were so, a logical contradiction occurs, hence the statement must be not so. This method is perhaps the most prevalent of mathematical proofs. A famous example of a proof by contradiction shows that 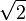$\sqrt{2}$ is an Irrational number:

Suppose that 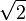$\sqrt{2}$ is a rational number, so $\sqrt{2} = {a\over b}$ where a and b are non-zero integers with no common factor (definition of a rational number). Thus, $b\sqrt{2} = a$ . Squaring both sides yields 2b² = a². Since 2 divides the left hand side, 2 must also divide the right hand side (as they are equal and both integers). So a² is even, which implies that a must also be even. So we can write a = 2c, where c is also an integer. Substitution into the original equation yields 2b² = (2c)² = 4c². Dividing both sides by 2 yields b² = 2c². But then, by the same argument as before, 2 divides b², so b must be even. However, if a and b are both even, they share a factor, namely 2. 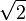This contradicts our assumption, so we are forced to conclude that $\sqrt{2}$ is an irrational number.

[edit] Proof by construction

Main article: Proof by construction

Proof by construction, or proof by example, is the construction of a concrete example with a property to show that something having that property exists. Joseph Liouville, for instance, proved the existence of transcendental numbers by constructing an explicit example.

[edit] Proof by exhaustion

Main article: Proof by exhaustion

In proof by exhaustion, the conclusion is established by dividing it into a finite number of cases and proving each one separately. The number of cases sometimes can become very large. For example, the first proof of the four colour theorem was a proof by exhaustion with 1,936 cases. This proof was controversial because the majority of the cases were checked by a computer program, not by hand. The shortest known proof of the four colour theorem today still has over 600 cases.

[edit] Probabilistic proof

Main article: Probabilistic method

A probabilistic proof is one in which an example is shown to exist, with certainty, by using methods of probability theory. This is not to be confused with an argument that a theorem is 'probably' true. The latter type of reasoning can be called a 'plausibility argument' and is not a proof; in the case of the Collatz conjecture it is clear how far that is from a genuine proof.^[5] Probabilistic proof, like proof by construction, is one of many ways to show existence theorems.

[edit] Combinatorial proof

Main article: Combinatorial proof

A combinatorial proof establishes the equivalence of different expressions by showing that they count the same object in different ways. Often a bijection between two sets is used to show that the expressions for their two sizes are equal. Alternatively, a double counting argument provides two different expressions for the size of a single set, again showing that the two expressions are equal.

[edit] Nonconstructive proof

Main article: Nonconstructive proof

A nonconstructive proof establishes that a certain mathematical object must exist (e.g. "Some X satisfies f(X)"), without explaining how such an object can be found. Often, this takes the form of a proof by contradiction in which the nonexistence of the object is proven to be impossible. In contrast, a constructive proof establishes that a particular object exists by providing a method of finding it. A famous example of a nonconstructive proof shows that there exist two irrational numbers $a$ and $b$ such that $a b$ is a rational number:

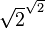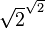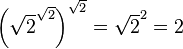Either $\sqrt{2}^{\sqrt{2}}$ is a rational number and we are done (take $a=b=\sqrt{2}$ ), or $\sqrt{2}^{\sqrt{2}}$ is irrational so we can write $a=\sqrt{2}^{\sqrt{2}}$ and $b=\sqrt{2}$ . This then gives $\left (\sqrt{2}^{\sqrt{2}}\right )^{\sqrt{2}}=\sqrt{2}^{2}=2$ , which is thus a rational of the form

a b .

[edit] Visual proof

Visual proof for the (3, 4, 5) triangle as in the Chou Pei Suan Ching 500–200 BC.

Although not a formal proof, a visual demonstration of a mathematical theorem is sometimes called a "proof without words". The picture at right is an example of a historic visual proof of the Pythagorean theorem in the case of the (3,4,5) triangle.

[edit] Elementary proof

Main article: Elementary proof

An elementary proof is a proof which only uses basic techniques. More specifically, the term is used in number theory to refer to proofs that make no use of complex analysis. For some time it was thought that certain theorems, like the prime number theorem, could only be proved using "higher" mathematics. However, over time, many of these results have been reproved using only elementary techniques.

[edit] Two-column proof

A two-column proof published in 1913

A particular form of proof using two parallel columns is often used in elementary geometry classes.^[6] The proof is written as a series of lines in two columns. In each line, the left hand column contains propositions (or sometimes called statements), while the right hand column contains a brief explanation of how this proposition is either an axiom, a hypothesis, or can be obtained from previous lines (or sometimes just called "reasons").

[edit] Statistical proofs in pure mathematics

Main article: Statistical proof

The expression "statistical proof" may be used technically or colloquially in areas of pure mathematics, such as involving cryptography, chaotic series, and probabilistic or analytic number theory.^[7]^[8]^[9] It is less commonly used to refer to a mathematical proof in the branch of mathematics known as mathematical statistics. See also "Statistical proof using data" section below.[4].

[edit] Computer-assisted proofs

Main article: Computer-assisted proof

Until the twentieth century it was assumed that any proof could, in principle, be checked by a competent mathematician to confirm its validity.^[1] However, computers are now used both to prove theorems and to carry out calculations that are too long for any human or team of humans to check; the first proof of the four color theorem is an example of a computer-assisted proof. Some mathematicians are concerned that the possibility of an error in a computer program or a run-time error in its calculations calls the validity of such computer-assisted proofs into question. In practice, the chances of an error invalidating a computer-assisted proof can be reduced by incorporating redundancy and self-checks into calculations, and by developing multiple independent approaches and programs.

[edit] Undecidable statements

A statement that is neither provable nor disprovable from a set of axioms is called undecidable (from those axioms). One example is the parallel postulate, which is neither provable nor refutable from the remaining axioms of Euclidean geometry.

Mathematicians have shown there are many statements that are neither provable nor disprovable in Zermelo-Fraenkel set theory with the axiom of choice (ZFC), the standard system of set theory in mathematics (assuming that ZFC is consistent); see list of statements undecidable in ZFC.

Gödel's (first) incompleteness theorem shows that many axiom systems of mathematical interest will have undecidable statements.

[edit] Heuristic mathematics and experimental mathematics

Main article: Experimental mathematics

While early mathematicians such as Eudoxus of Cnidus did not use proofs, from Euclid to the foundational mathematics developments of the late 19th and 20th centuries, proofs were an essential part of mathematics.^[10] With the increase in computing power in the 1960’s, significant work began to be done investigating mathematical objects outside of the proof-theorem framework,^[11] in experimental mathematics. Early pioneers of these methods intended the work ultimately to be embedded in a classical proof-theorem framework, e.g. the early development of fractal geometry^[12], which was ultimately so embedded.

[edit] Related concepts

[edit] Colloquial use of "mathematical proof"

The expression "mathematical proof" is used by lay people to refer to using mathematical methods or arguing with mathematical objects, such as numbers, to demonstrate something about everyday life, or when data used in an argument are numbers. It is sometime also used to mean a "statistical proof" (below), especially when used to argue from data.

[edit] Statistical proof using data

Main article: Statistical proof

"Statistical proof" from data refers to the application of statistics, data analysis, or Bayesian analysis to infer propositions regarding the probability of data. While using mathematical proof to establish theorems in statistics, it is usually not a mathematical proof in that the assumpions from which probability statements are derived require empirical evidence from outside mathematics to verify. In physics, in addition to statistical methods, "statistical proof" can refer to the specialized mathematical methods of physics applied to analyze data in a particle physics experiment or observational study in cosmology. "Statistical proof" may also refer to raw data or a convincing diagram involving data, such as scatter plots, when the data or diagram is adequately convincing without further anaylisis.

[edit] Inductive logic proofs and Bayesian analysis

Main articles: Inductive logic and Bayesian analysis

Proofs using inductive logic, while considered mathematical in nature, seek to establish propositions with a degree of certainty, which acts in a similar manner to probability, and may be less than one certainty. Bayesian analysis establishes assertions as to the degree of a person's subjective belief. Inductive logic should not be confused with mathematical induction.

[edit] Proofs as mental objects

Main articles: Psychologism and Language of thought

Psychologism views mathematical proofs as psychological or mental objects. Mathematician philosophers, such as Leibnitz, Frege, and Carnap, have attempted to develop a semantics for what they considered to be the language of thought, whereby standards of mathematical proof might be applied to empirical science.

[edit] Influence of mathematical proof methods outside mathematics

Philosopher-mathematicians such as Schopenhauer have attempted to formulate philosophical arguments in an axiomatic manner, whereby mathematical proof standards could be applied to argumentation in general philosophy. Other mathematician-philosophers have tried to use standards of mathematical proof and reason, without empiricism, to arrive at statements outside of mathematics, but having the certainty of propositions deduced in a mathematical proof, such as Descarte’s cogito argument. Kant and Frege considered mathematical proof to be analytic apriori.

[edit] Ending a proof

Main article: Q.E.D.

Sometimes, the abbreviation "Q.E.D." is written to indicate the end of a proof. This abbreviation stands for "Quod Erat Demonstrandum", which is Latin for "that which was to be demonstrated". A more common alternative is to use a square or a rectangle, such as □ or ∎, known as a "tombstone" or "halmos". Often, "which was to be shown" is verbally stated when writing "QED", "□", or "∎" in an oral presentation on a board.

[edit] See also

[edit] References

^ ^a ^b The History and Concept of Mathematical Proof, Steven G. Krantz. 1. February 5, 2007
^ The Emergence of Probability, Ian Hacking
^ Buss, 1997, p. 3
^ Proof by induction, University of Warwick Glossary of Mathematical Terminology
^ While most mathematicians do not think that probabilistic evidence ever counts as a genuine mathematical proof, a few mathematicians and philosophers have argued that at least some types of probabilistic evidence (such as Rabin’s probabilistic algorithm for testing primality) are as good as genuine mathematical proofs. See, for example, Davis, Philip J. (1972), "Fidelity in Mathematical Discourse: Is One and One Really Two?" American Mathematical Monthly 79:252-63. Fallis, Don (1997), "The Epistemic Status of Probabilistic Proof." Journal of Philosophy 94:165-86.
^ Patricio G. Herbst, Establishing a Custom of Proving in American School Geometry: Evolution of the Two-Column Proof in the Early Twentieth Century, Educational Studies in Mathematics, Vol. 49, No. 3 (2002), pp. 283-312,
^ “in number theory and commutative algebra... in particular the statistical proof of the lemma.” [1]
^ “Whether constant π (i.e., pi) is normal is a confusing problem without any strict theoretical demonstration except for some statistical proof”” (Derogatory use.)[2]
^ “these observations suggest a statistical proof of Goldbach's conjecture with very quickly vanishing probability of failure for large E” [3]
^ "What to do with the pictures? Two thoughts surfaced: the first was that they were unpublishable in the standard way, there were no theorems only very suggestive pictures. They furnished convincing evidence for many conjectures and lures to further exploration, but theorems were coins of the realm ant the conventions of that day dictated that journals only published theorems", David Mumford, Caroline Series and David Wright, Indra’s Pearls, 2002
^ "Mandelbrot, working at the IBM Research Laboratory, did some computer simulations for these sets on the reasonable assumption that, if you wanted to prove something, it might be helpful to know the answer ahead of time."A Note on the History of Fractals,
^ "… brought home again to Benoit [Mandelbrot] that there was a ‘mathematics of the eye’, that visualization of a problem was as valid a method as any for finding a solution. Amazingly, he found himself alone with this conjecture. The teaching of mathematics in France was dominated by a handful of dogmatic mathematicians hiding behind the pseudonym ‘Bourabki’… ", Introducing Fractal Geometry, Nigel Lesmoir-Gordon

[edit] Sources

Polya, G. Mathematics and Plausible Reasoning. Princeton University Press, 1954.
Fallis, Don (2002) “What Do Mathematicians Want? Probabilistic Proofs and the Epistemic Goals of Mathematicians.” Logique et Analyse 45:373-88.
Franklin, J. and Daoud, A. Proof in Mathematics: An Introduction. Quakers Hill Press, 1996. ISBN 1-876192-00-3
Solow, D. How to Read and Do Proofs: An Introduction to Mathematical Thought Processes. Wiley, 2004. ISBN 0-471-68058-3
Velleman, D. How to Prove It: A Structured Approach. Cambridge University Press, 2006. ISBN 0-521-67599-5

[edit] External links

What are mathematical proofs and why they are important?
How To Write Proofs by Larry W. Cusick
How to Write a Proof by Leslie Lamport, and the motivation of proposing such a hierarchical proof style.
Proofs in Mathematics: Simple, Charming and Fallacious
The Seventeen Provers of the World, ed. by Freek Wiedijk, foreword by Dana S. Scott, Lecture Notes in Computer Science 3600, Springer, 2006, ISBN 3-540-30704-4. Contains formalized versions of the proof that $\sqrt{2}$ is irrational in several automated proof systems.
What is Proof? Thoughts on proofs and proving.
ProofWiki.org An online compendium of mathematical proofs.
planetmath.org A wiki style encyclopedia of proofs
A lesson about proofs, in a course from Wikiversity

[Krantz-0] The History and Concept of Mathematical Proof, Steven G. Krantz. 1. February 5, 2007

[1] The Emergence of Probability, Ian Hacking

[2] Buss, 1997, p. 3

[3] Proof by induction, University of Warwick Glossary of Mathematical Terminology

[4] While most mathematicians do not think that probabilistic evidence ever counts as a genuine mathematical proof, a few mathematicians and philosophers have argued that at least some types of probabilistic evidence (such as Rabin’s probabilistic algorithm for testing primality) are as good as genuine mathematical proofs. See, for example, Davis, Philip J. (1972), "Fidelity in Mathematical Discourse: Is One and One Really Two?" American Mathematical Monthly 79:252-63. Fallis, Don (1997), "The Epistemic Status of Probabilistic Proof." Journal of Philosophy 94:165-86.

[5] Patricio G. Herbst, Establishing a Custom of Proving in American School Geometry: Evolution of the Two-Column Proof in the Early Twentieth Century, Educational Studies in Mathematics, Vol. 49, No. 3 (2002), pp. 283-312,

[6] “in number theory and commutative algebra... in particular the statistical proof of the lemma.” [1]

[7] “Whether constant π (i.e., pi) is normal is a confusing problem without any strict theoretical demonstration except for some statistical proof”” (Derogatory use.)[2]

[8] “these observations suggest a statistical proof of Goldbach's conjecture with very quickly vanishing probability of failure for large E” [3]

[9] "What to do with the pictures? Two thoughts surfaced: the first was that they were unpublishable in the standard way, there were no theorems only very suggestive pictures. They furnished convincing evidence for many conjectures and lures to further exploration, but theorems were coins of the realm ant the conventions of that day dictated that journals only published theorems", David Mumford, Caroline Series and David Wright, Indra’s Pearls, 2002

[10] "Mandelbrot, working at the IBM Research Laboratory, did some computer simulations for these sets on the reasonable assumption that, if you wanted to prove something, it might be helpful to know the answer ahead of time."A Note on the History of Fractals,

[11] "… brought home again to Benoit [Mandelbrot] that there was a ‘mathematics of the eye’, that visualization of a problem was as valid a method as any for finding a solution. Amazingly, he found himself alone with this conjecture. The teaching of mathematics in France was dominated by a handful of dogmatic mathematicians hiding behind the pseudonym ‘Bourabki’… ", Introducing Fractal Geometry, Nigel Lesmoir-Gordon

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]