Church encoding

From Wikipedia, the free encyclopedia

In mathematics, Church encoding is a means of embedding data and operators into the lambda calculus, the most familiar form being the Church numerals, a representation of the natural numbers using lambda notation. The method is named for Alonzo Church, who first encoded data in the lambda calculus this way.

Terms that are usually considered primitive in other notations (such as integers, booleans, pairs, lists, and tagged unions) are mapped to higher-order functions under Church encoding; the Church-Turing thesis asserts that any computable operator (and its operands) can be represented under Church encoding.

Many students of mathematics are familiar with Gödel numbering members of a set; Church encoding is an equivalent operation defined on lambda abstractions instead of natural numbers.

[edit] Church numerals

Church numerals are the representations of natural numbers under Church encoding. The higher-order function that represents natural number $n$ is a function that maps any other function $f$ to its n-fold composition. In simpler terms, the "value" of the numeral is equivalent to the number of times the function encapsulates x.

$f^n = f \circ f \circ \cdots \circ f.\,$

[edit] Definition

Church numerals 0, 1, 2, ..., are defined as follows in the lambda calculus:

0 ≡ λf.λx. x

1 ≡ λf.λx. f x

2 ≡ λf.λx. f (f x)

3 ≡ λf.λx. f (f (f x))

...

n ≡ λf.λx. fⁿ x

...

That is, the natural number $n$ is represented by the Church numeral n, which has the property that for any lambda-terms F and X,

n F X =_β Fⁿ X

[edit] Computation with Church numerals

In the lambda calculus, numeric functions are representable by corresponding functions on Church numerals. These functions can be implemented in most functional programming languages (subject to type constraints) by direct translation of lambda terms.

The addition function $\scriptstyle\operatorname{plus}(m,n)=m+n$ uses the identity $f (m + n) (x) = f m (f n (x))$ .

plus ≡ λm.λn.λf.λx. m f (n f x)

The successor function $\scriptstyle\operatorname{succ}(n)=n+1$ is β-equivalent to (plus 1).

succ ≡ λn.λf.λx. f (n f x)

The multiplication function 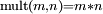$\scriptstyle\operatorname{mult}(m,n)=m*n$ uses the identity $f (m * n) = (f m) n$ .

mult ≡ λm.λn.λf. n (m f)

The exponentiation function $\scriptstyle\exp(m,n)=m^n$ is straightforward given our definition of church numerals.

exp ≡ λm.λn. n m

The predecessor function $\operatorname{pred}(n) = \begin{cases} 0 & \mbox{if }n=0, \\ n-1 & \mbox{otherwise}\end{cases}$ works by generating an $n$ -fold composition of functions that each apply their argument g to f; the base case discards its copy of f and returns x.

pred ≡ λn.λf.λx. n (λg.λh. h (g f)) (λu. x) (λu. u)

The subtraction function can be written based on the predecessor function.

sub ≡ λm.λn. (m pred) n

The zero predicate can be written as:

zero? ≡ λn. n (λx.F) T

Now:

zero? 0 =_β T if n =_β 0.

zero? n =_β F if n ≠_β 0, provided n is a Church numeral and where ≠_β is the negation of =_β restricted to reducible lambda terms.

T and F can be arbitrary terms, for example the two Booleans as described elsewhere in this article.

[edit] Translation with other representations

Most real-world languages have support for machine-native integers; the church and unchurch functions (given here in Haskell) convert between nonnegative integers and their corresponding church numerals. Implementations of these conversions in other languages are similar.


type Church a = (a -> a) -> a -> a

church :: Integer -> Church a
church 0 = \f -> \x -> x
church n = \f -> \x -> f (church (n-1) f x)

unchurch :: Church Integer -> Integer
unchurch n = n (\x -> x + 1) 0

In Haskell, the \ corresponds to the λ of Lambda calculus.

[edit] Church booleans

Church booleans are the Church encoding of the boolean values true and false. Some programming languages use these as an implementation model for boolean arithmetic; examples are Smalltalk and Pico. The boolean values are represented as functions of two values that evaluate to one or the other of their arguments.

Formal definition in lambda calculus:

true ≡ λa.λb. a

false ≡ λa.λb. b

Note that this definition allows predicates (i.e. functions returning logical values) to directly act as if-clauses, e.g. if predicate is a unary predicate,

predicate x then-clause else-clause

evaluates to then-clause if predicate x evaluates to true, and to else-clause if predicate x evaluates to false.

Functions of boolean arithmetic can be derived for Church booleans:

and ≡ λm.λn. m n m

or ≡ λm.λn. m m n

not ≡ λm.λa.λb. m b a

xor ≡ λm.λn.λa.λb. m (n b a) (n a b)

Some examples:

and true false ≡ (λm.λn. m n m) (λa.λb. a) (λa.λb. b) ≡ (λa.λb. a) (λa.λb. b) (λa.λb. a) ≡ (λa.λb. b) ≡ false

or true false ≡ (λm.λn. m m n) (λa.λb. a) (λa.λb. b) ≡ (λa.λb. a) (λa.λb. a) (λa.λb. b) ≡ (λa.λb. a) ≡ true

not true ≡ (λm.λa.λb. m b a) (λa.λb. a) ≡ (λa.λb. (λa.λb. a) b a) ≡ (λa.λb. b) ≡ false

[edit] Church pairs

[edit] List encodings

An encoding of (immutable) lists of varying length must define a constructor for creating an empty list (nil), an operation testing whether or not a list is empty (isnil), an operation to prepend a given value to a (possibly empty) list (cons), and two operations to determine the first element and the list of the remaining elements of a nonempty list (head and tail).

[edit] Church pairs

A nonempty list can basically be encoded by a Church pair with the head of the list stored in the first component of the pair and the tail of the list in the second component. However, special care is needed to unambiguously encode the empty list. This can be achieved by encapsulating any individual list node with another pair with the second component containing the list node and the first component containing a Church boolean which is true for the empty list and false otherwise, similarly to a tagged union. Using this idea the basic list operations can be defined like this:^[1]

nil ≡ pair true true

isnil ≡ fst

cons ≡ λh.λt.pair false (pair h t)

head ≡ λz.fst (snd z)

tail ≡ λz.snd (snd z)

The second component of the pair enconding nil is never used provided that head and tail are only applied to nonempty lists.

[edit] Higher-order-function

As an alternative to the encoding using Church pairs, a list can be encoded by identifying it with its right fold function. For example, a list of three elements x, y and z can be encoded by a higher-order function which when applied to a combinator c and a value n returns c x (c y (c z n))).

nil ≡ λc.λn.n

isnil ≡ λl.l (λh.λt.false) true

cons ≡ λh.λt.λc.λn.c h (t c n)

head ≡ λl.l (λh.λt.h) false

tail ≡ λl.fst (l (λx.λp.pair (snd p) (cons x (snd p))) (pair nil nil))

[edit] See also

Lambda calculus
System F for Church numerals in a typed calculus
Mogensen-Scott encoding

[edit] References

^ Pierce, Benjamin C. (2002). Types and Programming Languages. MIT Press. pp. 500. ISBN 978-0262162098.

[0] Pierce, Benjamin C. (2002). Types and Programming Languages. MIT Press. pp. 500. ISBN 978-0262162098.

[1]

Church encoding

From Wikipedia, the free encyclopedia

Contents

[edit] Church numerals

[edit] Definition

[edit] Computation with Church numerals

[edit] Translation with other representations

[edit] Church booleans

[edit] Church pairs

[edit] List encodings

[edit] Church pairs

[edit] Higher-order-function

[edit] See also

[edit] References

Views

Personal tools

Navigation

Search

Interaction

Toolbox

Languages