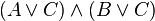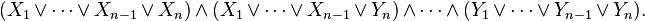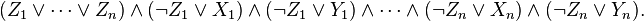Conjunctive normal form

From Wikipedia, the free encyclopedia

In boolean logic, a formula is in conjunctive normal form (CNF) if it is a conjunction of clauses, where a clause is a disjunction of literals. As a normal form, it is useful in automated theorem proving. It is similar to the canonical product of sums form used in circuit theory.

All conjunctions of literals and all disjunctions of literals are in CNF, as they can be seen as conjunctions of one-literal clauses and conjunctions of a single clause, respectively. As in the disjunctive normal form (DNF), the only propositional connectives a formula in CNF can contain are and, or, and not. The not operator can only be used as part of a literal, which means that it can only precede a propositional variable.

[edit] Examples and counterexamples

All of the following formulas are in CNF:

$\neg A \wedge (B \vee C)$

$(A \vee B) \wedge (\neg B \vee C \vee \neg D) \wedge (D \vee \neg E)$

$A \wedge B.$

The last formula is in CNF because it can be seen as the conjunction of the two single-literal clauses $A$ and $B$ . Incidentally, this formula is also in disjunctive normal form. The following formulae are not in CNF:

$\neg (B \vee C)$

$(A \wedge B) \vee C$

$A \wedge (B \vee (D \wedge E)).$

The above three formulas are respectively equivalent to the following three formulas that are in conjunctive normal form:

$\neg B \wedge \neg C$

$(A \vee C) \wedge (B \vee C)$

$A \wedge (B \vee D) \wedge (B \vee E).$

[edit] Conversion into CNF

Every propositional formula can be converted into an equivalent formula that is in CNF. This transformation is based on rules about logical equivalences: the double negative law, the De Morgan's laws, and the distributive law.

Since all logical formulas can be converted into an equivalent formula in conjunctive normal form, proofs are often based on the assumption that all formulae are CNF. However, in some cases this conversion to CNF can lead to an exponential explosion of the formula. For example, translating the following non-CNF formula in CNF produces a formula with $2 n$ clauses:

$(X_1 \wedge Y_1) \vee (X_2 \wedge Y_2) \vee \dots \vee (X_n \wedge Y_n).$

In particular, the generated formula is:

$(X_1 \vee \cdots \vee X_{n-1} \vee X_n) \wedge (X_1 \vee \cdots \vee X_{n-1} \vee Y_n) \wedge \cdots \wedge (Y_1 \vee \cdots \vee Y_{n-1} \vee Y_n).$

In words, this formula contains $2 n$ clauses: in each clause contains either $X i$ or $Y i$ for each $i$ .

Transformations of formulas in CNF preserving satisfiability rather than equivalence and not producing an exponential increase of size exist. These transformations are guaranteed to only linearly increase the size of the formula, but introduce new variables. For example, the above formula can be put in CNF by adding variables $Z_1,\ldots,Z_n$ as follows:

$(Z_1 \vee \cdots \vee Z_n) \wedge (\neg Z_1 \vee X_1) \wedge (\neg Z_1 \vee Y_1) \wedge \cdots \wedge (\neg Z_n \vee X_n) \wedge (\neg Z_n \vee Y_n).$

An interpretation satisfies this formula only if at least one of the new variables is true. If this variable is $Z i$ , then both $X i$ and $Y i$ are true as well. This means that every model that satisfies this formula also satisfies the original one. On the other hand, only some of the models of the original formula satisfy this one: since the $Z i$ are not mentioned in the original formula, their values are irrelevant to satisfaction of it, which is not the case in the last formula. This means that the original formula and the result of the translation are equisatisfiable but not equivalent.

An alternative translation includes also the clauses $Z_i \vee \neg X_i \vee \neg Y_i$ . With these clauses, the formula implies $Z_i \equiv X_i \wedge Y_i$ ; this formula is often regarded to "define" $Z i$ to be a name for $X_i \wedge Y_i$ .

[edit] First-order logic

In first order logic, conjunctive normal form can be taken further to yield the clausal normal form of a logical formula, which can be then used to perform first-order resolution.

[edit] Computational complexity

An important set of problems in computational complexity involves finding assignments to the variables of a boolean formula expressed in Conjunctive Normal Form, such that the formula is true. The k-SAT problem is the problem of finding a satisfying assignment to a boolean formula expressed in CNF such that each disjunction contains at most k variables. 3-SAT is NP-complete (like any other k-SAT problem with k>2) while 2-SAT is known to have solution in polynomial time.

[edit] Converting from first-order logic

To convert first-order logic to CNF:

Convert to Negation normal form.
1. Eliminate implications: convert $x \rightarrow y$ to $\neg x \vee y$
2. Move NOTs inwards.
Standardize variables
Skolemize the statement
Drop universal quantifiers
Distribute ANDs over ORs.

(Artificial Intelligence: A modern Approach [1995...] Russel and Norvig)

[edit] See also

[edit] External links

Conjunctive normal form

From Wikipedia, the free encyclopedia

Contents

[edit] Examples and counterexamples

[edit] Conversion into CNF

[edit] First-order logic

[edit] Computational complexity

[edit] Converting from first-order logic

[edit] See also

[edit] External links

Views

Personal tools

Navigation

Search

Interaction

Toolbox

Languages