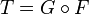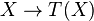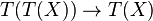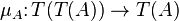Monad (category theory)
From Wikipedia, the free encyclopedia
In category theory, a monad or triple is an (endo-)functor, together with two associated natural transformations. They are important in the theory of pairs of adjoint functors, and they generalize closure operators on posets to arbitrary categories.
The notion of "algebras for a monad" generalizes classical notions from universal algebra, and in this sense, monads can be thought of as "theories".
Contents |
[edit] Introduction
If F and G are a pair of adjoint functors, with F left adjoint to G, then the composition  is a monad. Therefore, a monad is a functor from a category to itself. If F and G are inverse functors the corresponding monad is the identity functor. In general adjunctions are not equivalences — they relate categories of different natures. The monad theory matters as part of the effort to capture what it is that adjunctions 'preserve'. The other half of the theory, of what can be learned likewise from consideration of
is a monad. Therefore, a monad is a functor from a category to itself. If F and G are inverse functors the corresponding monad is the identity functor. In general adjunctions are not equivalences — they relate categories of different natures. The monad theory matters as part of the effort to capture what it is that adjunctions 'preserve'. The other half of the theory, of what can be learned likewise from consideration of  , is discussed under the dual theory of comonads.
, is discussed under the dual theory of comonads.
The monad axioms can be seen at work in a simple example: let G be the forgetful functor from the category Grp of groups to the category Set of sets. Then as F we can take the free group functor.
This means that the monad
takes a set X and returns the underlying set of the free group Free(X). In this situation, we are given two natural morphisms:
by including any set X in Free(X) in the natural way, as strings of length 1. Further,
can be made out of a natural concatenation of 'strings of strings'. This amounts to two natural transformations
and
They will satisfy some axioms about identity and associativity that result from the adjunction properties.
Those axioms are formally similar to the monoid axioms. They are taken as the definition of a general monad (not assumed a priori to be connected to an adjunction) on a category.
If we specialize to categories arising from partially ordered sets  (with a single morphism from x to y iff
(with a single morphism from x to y iff 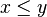 ), then the formalism becomes much simpler: adjoint pairs are Galois connections and monads are closure operators.
), then the formalism becomes much simpler: adjoint pairs are Galois connections and monads are closure operators.
Every monad arises from some adjunction, in fact typically from many adjunctions. Two constructions introduced below, the Kleisli category and the category of Eilenberg-Moore algebras, are extremal solutions of the problem of constructing an adjunction that gives rise to a given monad.
The example about free groups given above can be generalized to any type of algebra in the sense of a variety of algebras in universal algebra. Thus, every such type of algebra gives rise to a monad on the category of sets. Importantly, the algebra type can be recovered from the monad (as the category of Eilenberg-Moore algebras), so monads can also be seen as generalizing universal algebras. Even more generally, any adjunction is said to be monadic (or tripleable) if it shares this property of being (equivalent to) the Eilenberg-Moore category of its associated monad. Consequently Beck's monadicity theorem, which gives a criterion for monadicity, can be used to show that an arbitrary adjunction can be treated as a category of algebras in this way.
The language of monads belongs to the school of Mac Lane, and members of the school of Grothendieck often only work with adjoint functors, not mentioning monads directly.
[edit] Formal definition
If C is a category, a monad on C consists of a functor 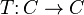 together with two natural transformations:
together with two natural transformations:  (where 1C denotes the identity functor on C) and
(where 1C denotes the identity functor on C) and 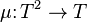 (where T2 is the functor
(where T2 is the functor  from C to C). These are required to fulfill the following conditions (sometimes called coherence conditions):
from C to C). These are required to fulfill the following conditions (sometimes called coherence conditions):
 (as natural transformations
(as natural transformations 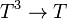 );
);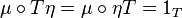 (as natural transformations
(as natural transformations  ; here 1T denotes the identity transformation from T to T).
; here 1T denotes the identity transformation from T to T).
With commutative diagrams:
See the article on natural transformations for the explanation of the notations Tμ and μT, or see below the commutative diagrams not using these notions:
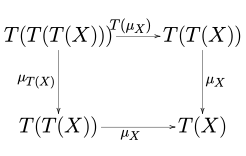 |
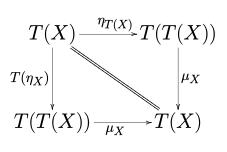 |
The first axiom is akin to the associativity in monoids, the second axiom to the existence of an identity element. Indeed, a monad on C can alternatively be defined as a monoid in the category 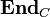 whose objects are the endofunctors of C and whose morphisms are the natural transformations between them, with the monoidal structure induced by the composition of endofunctors.
whose objects are the endofunctors of C and whose morphisms are the natural transformations between them, with the monoidal structure induced by the composition of endofunctors.
[edit] Comonads and their importance
The categorical dual definition is a formal definition of a comonad (or cotriple); this can be said quickly in the terms that a comonad for a category C is a monad for the opposite category Cop. It is therefore a functor U from C to itself, with a set of axioms for counit and comultiplication that come from reversing the arrows everywhere in the definition just given.
Since a comonoid is not a basic structure in abstract algebra, this is less familiar at an immediate level.
The importance of the definition comes in a class of theorems from the categorical (and algebraic geometry) theory of descent. What was realised in the period 1960 to 1970 is that recognising the categories of coalgebras for a comonad was an important tool of category theory (particularly topos theory). The results involved are based on Beck's theorem. Roughly what goes on is this: while it is simple set theory that a surjective mapping of sets is as good as the imposition of the equivalence relation 'in the same fiber', for geometric morphisms what you should do is pass to such a coalgebra subcategory.
[edit] Examples
The most important examples to think about when hearing the term "monad" are the free group example mentioned above, and closure operators. Another example, on the category  : for a set A let T(A) be the power set of A and for a function
: for a set A let T(A) be the power set of A and for a function  let T(f) be the function between the power sets induced by taking direct images under f. For every set A, we have a map
let T(f) be the function between the power sets induced by taking direct images under f. For every set A, we have a map 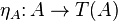 , which assigns to every element a of A the singleton {a}. A function
, which assigns to every element a of A the singleton {a}. A function
can be given as follows: if L is a set whose elements are subsets of A, then taking the union of these subsets gives a subset ηA(L) of A. These data describe a monad.
[edit] Algebras for a monad
Suppose that (T,η,μ) is a given monad on a category C.
A T-algebra (x,h) is an object x of C together with an arrow 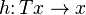 of C called the structure map of the algebra such that the diagrams
of C called the structure map of the algebra such that the diagrams
 |
and |  |
commute.
A morphism 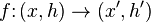 of T-algebras is an arrow
of T-algebras is an arrow  of C such that the diagram
of C such that the diagram
commutes.
The category CT of T-algebras and their morphisms is called the Eilenberg-Moore category or category of (Eilenberg-Moore) algebras of the monad T.
Given the monad T, there exists another "canonical" category CT called the Kleisli category of the monad T. Its objects are the objects of C and its arrows from x to y are the arrows 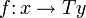 in C. The identity on an object x is the unit ηx, and the composite
in C. The identity on an object x is the unit ηx, and the composite  of two arrows
of two arrows 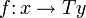 and
and 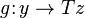 is given by
is given by 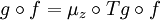 . This category is equivalent to the category of free algebras for the monad T, i. e. the full subcategory of CT whose objects are of the form (Tx,μx), for x an object of C. The Kleisli category is named for mathematician Heinrich Kleisli.
. This category is equivalent to the category of free algebras for the monad T, i. e. the full subcategory of CT whose objects are of the form (Tx,μx), for x an object of C. The Kleisli category is named for mathematician Heinrich Kleisli.
[edit] Monads and adjunctions
An adjunction  between two categories C and D (where
between two categories C and D (where 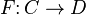 is left adjoint to
is left adjoint to  and η and
and η and  are respectively the unit and the counit) always defines a monad
are respectively the unit and the counit) always defines a monad  .
.
Conversely, it is interesting to consider the adjunctions which define a given monad (T,η,μ) this way. Let 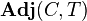 be the category whose objects are the adjunctions
be the category whose objects are the adjunctions 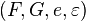 such that
such that 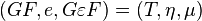 and whose arrows are the morphisms of adjunctions which are the identity on C. Then this category has
and whose arrows are the morphisms of adjunctions which are the identity on C. Then this category has
- an initial object
 , where CT is the Kleisli category,
, where CT is the Kleisli category, - a terminal object
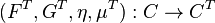 , where CT is the Eilenberg-Moore category.
, where CT is the Eilenberg-Moore category.
An adjunction  between two categories C and D is a monadic adjunction when the category D is equivalent to the Eilenberg-Moore category CT for the monad T = GF. By extension, a functor
between two categories C and D is a monadic adjunction when the category D is equivalent to the Eilenberg-Moore category CT for the monad T = GF. By extension, a functor  is said to be monadic if it has a left adjoint F forming a monadic adjunction. Beck's monadicity theorem gives a characterization of monadic functors.
is said to be monadic if it has a left adjoint F forming a monadic adjunction. Beck's monadicity theorem gives a characterization of monadic functors.
[edit] Uses
Monads are used in functional programming to express types of sequential computation (sometimes with side-effects). See monads in functional programming, and the more mathematically oriented Wikibook module b:Haskell/Category_theory.
In categorical logic, an analogy has been drawn between the monad-comonad theory, and modal logic[citation needed].
[edit] Generalization
It is possible to define monads in a 2-category C. Monads described above are monads for  .
.
[edit] See also
- Distributive law between monads
- Strong monad
- Monad for other meanings of the term.
[edit] References
- Daniele Turi: Category Theory Lecture Notes (1996-2001), based on MacLane's book "Categories for the Working Mathematician"
- Michael Barr and Charles Wells: Category Theory Lecture Notes (1999), based on their book "Category Theory for Computing Science"
[edit] External links
- Monads Five short lectures (with one appendix).
- John Baez's This Week's Finds in Mathematical Physics (Week 89) covers monads in 2-categories.