Monty Hall problem
From Wikipedia, the free encyclopedia
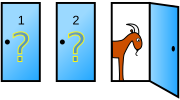
The Monty Hall problem is a probability puzzle based on the American television game show Let's Make a Deal. The name comes from the show's host, Monty Hall. The problem is also called the Monty Hall paradox, as it is a veridical paradox in that the solution is counterintuitive.
A well-known statement of the problem was published in Parade magazine:
Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say No. 3, which has a goat. He then says to you, "Do you want to pick door No. 2?" Is it to your advantage to switch your choice? (Whitaker 1990)
Because there is no way for the player to know which of the two remaining unopened doors is the winning door, most people assume that each of these doors has an equal probability and conclude that switching does not matter. In fact, the player should switch — doing so doubles the probability of winning the car from 1/3 to 2/3.
Simple probability indicates that the player has a 2/3 chance of initially choosing a goat. Players who unconditionally stick to that choice therefore have only a 1/3 chance of winning the car. Players who unconditionally switch get the opposite of their original choice, so they have a 2/3 chance of winning a car.
When the problem and the solution appeared in Parade, approximately 10,000 readers, including nearly 1,000 with Ph.D.s, wrote to the magazine claiming the published solution was wrong. Some of the controversy was because the Parade version of the problem is technically ambiguous since it leaves certain aspects of the host's behavior unstated, for example whether the host must open a door and must make the offer to switch. Variants of the problem involving these and other assumptions have been published in mathematical literature.
The standard Monty Hall problem is mathematically equivalent to the earlier Three Prisoners problem and both are related to the much older Bertrand's box paradox. These and other problems involving unequal distributions of probability are notoriously difficult for people to solve correctly, and have led to numerous psychological studies. Even when given a completely unambiguous statement of the Monty Hall problem, explanations, simulations, and formal mathematical proofs, many people still meet the correct answer with disbelief.
Contents |
[edit] Problem
Steve Selvin wrote a letter to the American Statistician in 1975 describing a problem loosely based on the game show Let's Make a Deal (Selvin 1975a). In a subsequent letter he dubbed it the "Monty Hall problem" (Selvin 1975b). The problem is mathematically equivalent (Morgan et al., 1991) to the Three Prisoners Problem described in Martin Gardner's Mathematical Games column in Scientific American in 1959 (Gardner 1959a).
Selvin's Monty Hall problem was restated in its well-known form in a letter to Marilyn vos Savant's Ask Marilyn column in Parade:
Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say No. 3, which has a goat. He then says to you, "Do you want to pick door No. 2?" Is it to your advantage to switch your choice? (Whitaker 1990)
There are certain ambiguities in this formulation of the problem: it is unclear whether or not the host would always open another door, always offer a choice to switch, or even whether he would ever open the door revealing the car (Mueser and Granberg 1999). The standard analysis of the problem assumes that the host is indeed constrained always to open a door revealing a goat, always to make the offer to switch, and to open one of the remaining two doors randomly if the player initially picked the car (Barbeau 2000:87). Hence a more exact statement of the problem is as follows:
Suppose you're on a game show and you're given the choice of three doors. Behind one door is a car; behind the others, goats [that is, booby prizes]. The car and the goats were placed randomly behind the doors before the show. The rules of the game show are as follows: After you have chosen a door, the door remains closed for the time being. The game show host, Monty Hall, who knows what is behind the doors, now has to open one of the two remaining doors, and the door he opens must have a goat behind it. If both remaining doors have goats behind them, he chooses one randomly. After Monty Hall opens a door with a goat, he will ask you to decide whether you want to stay with your first choice or to switch to the last remaining door. Imagine that you chose Door 1 and the host opens Door 3, which has a goat. He then asks you "Do you want to switch to Door Number 2?" Is it to your advantage to change your choice? (Krauss and Wang 2003:10)
Note that the player may initially choose any of the three doors (not just Door 1), that the host opens a different door revealing a goat (not necessarily Door 3), and that he gives the player a second choice between the two remaining unopened doors. All situations with different door numbers form equivalent formulations of the problem and lead to the same conclusion.
[edit] Popular solution
A car and two goats are arranged behind three doors, with the position of the car being random and uniformly distributed among the three doors, and then the player initially picks a door. In the popular analysis, particular door numberings are not considered; the player, having chosen a door, has a 1/3 chance of having chosen the car, and a 1/3 chance of having chosen each particular goat. It is assumed that when the host opens a door to reveal a goat, this action does not give the player any new information about what is behind the door she has chosen, so the "proper Bayesian" still sees the probability of there being a car behind the chosen door as 1/3, and therefore the probability of a car behind the remaining door as 2/3. Switching doors thus wins the car with a probability of 2/3, so the player should always switch (Wheeler 1991; Mack 1992; Schwager 1994; vos Savant 1996:8).
[edit] Criticisms of the traditional solution
The above reasoning applies to all players at the start of the game without regard to which door the host opens, specifically before the host opens a particular door and gives the player the option to switch doors (Morgan et al. 1991). This means if a large number of players randomly choose whether to stay or switch, then approximately 1/3 of those choosing to stay with the initial selection and 2/3 of those choosing to switch would win the car. This result has been verified experimentally using computer and other simulation techniques (see Simulation below). Nevertheless, some statisticians cricitize the solution as being incorrect for the problem as stated, since the player's probability of winning by switching has not been evaluated in light of the extra information of which particular door the host opened to reveal a goat. In the example problem as stated, the player has chosen door 1 and the host has opened door 3; the door that the host opens potentially provides the player more information about the probability of the car being behind the originally chosen door, if the player has a probabilistic model of how the host chooses when he had a choice of which goat to reveal.
Under certain sets of assumptions on the game, including the host choosing randomly with equal probability between two goat doors when available, the contestant receives no new information that can change the 1/3 probability of winning by sticking to the initially chosen door (Granberg 1996), so this solution also correctly applies to the decision and probability for an individual game after the host opens a door. Under more general conditions, however, a more general solution is needed (Morgan et al. 1991).
[edit] Conditional solution
The popular solution above shows that the probability of winning by switching for all players who switch is 2/3, but this does not necessarily mean the probability of winning by switching is 2/3 given which door the host opens. This probability is a conditional probability (Morgan et al. 1991; Gillman 1992; Grinstead and Snell 2006:137). The difference is whether the analysis, as above, considers all possible scenarios or only the scenarios where the host opens a specific door. Another way to express the difference is whether the player must decide to switch before the host opens a door or is allowed to decide after seeing which door the host opens (Gillman 1992). The conditional probability may differ from the overall probability depending on the exact formulation of the problem.
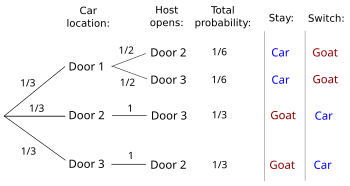
The conditional probability of winning by switching given which door the host opens can be determined referring to the expanded figure below or to an equivalent decision tree as shown to the right (Chun 1991; Grinstead and Snell 2006:137-138). For example, if the host opens Door 3 and the player switches, the player wins with overall probability 1/3 if the car is behind Door 2 and loses with overall probability 1/6 if the car is behind Door 1—the possibilities involving the host opening Door 2 do not apply. To convert these to conditional probabilities they are divided by their sum, so the conditional probability of winning by switching given the player picks Door 1 and the host opens Door 3 is (1/3)/(1/3 + 1/6), which is 2/3. This analysis depends on the constraint in the explicit problem statement that the host choose which door to open randomly if the player has initially selected the car.
Morgan et al. (1991) and Gillman (1992) both show a more general solution where the host is not constrained to pick randomly if the player has initially selected the car, which is how they both interpret the well known statement of the problem in Parade. They consider a scenario where the host chooses which door to open in this case with a preference expressed as a probability q, having a value between 0 and 1. If the host picks randomly q would be 1/2 and switching wins with probability 2/3 regardless of which door the host opens. If the player picks Door 1 and the host's preference for Door 3 is q, then in the case where the host opens Door 3 switching wins with overall probability 1/3 if the car is behind Door 2 and loses with overall probability (1/3)q if the car is behind Door 1. The conditional probability of winning by switching given the host opens Door 3 is therefore (1/3)/(1/3 + (1/3)q) which simplifies to 1/(1+q). Since q can vary between 0 and 1 this conditional probability can vary between 1/2 and 1. This means even without constraining the host to pick randomly if the player initially selects the car, the player is never worse off switching.
| Car hidden behind Door 3 | Car hidden behind Door 1 | Car hidden behind Door 2 | |
|---|---|---|---|
| Player initially picks Door 1 | |||
 |
 |
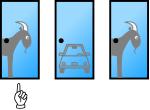 |
|
| Host must open Door 2 | Host randomly opens either goat door | Host must open Door 3 | |
 |
 |
 |
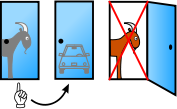 |
| Probability 1/3 | Probability 1/6 | Probability 1/6 | Probability 1/3 |
| Switching wins | Switching loses | Switching loses | Switching wins |
| If the host has opened Door 2, switching wins twice as often as staying | If the host has opened Door 3, switching wins twice as often as staying | ||
[edit] Sources of confusion
When first presented with the Monty Hall problem an overwhelming majority of people assume that each door has an equal probability and conclude that switching does not matter (Mueser and Granberg, 1999). Out of 228 subjects in one study, only 13% chose to switch (Granberg and Brown, 1995:713). In her book The Power of Logical Thinking, vos Savant (1996:15) quotes cognitive psychologist Massimo Piattelli-Palmarini as saying "... no other statistical puzzle comes so close to fooling all the people all the time" and "that even Nobel physicists systematically give the wrong answer, and that they insist on it, and they are ready to berate in print those who propose the right answer."
Most statements of the problem, notably the one in Parade Magazine, do not match the rules of the actual game show (Krauss and Wang, 2003:9), and do not fully specify the host's behavior or that the car's location is randomly selected (Granberg and Brown, 1995:712). Krauss and Wang (2003:10) conjecture that people make the standard assumptions even if they are not explicitly stated. Although these issues are mathematically significant, even when controlling for these factors nearly all people still think each of the two unopened doors has an equal probability and conclude switching does not matter (Mueser and Granberg, 1999). This "equal probability" assumption is a deeply rooted intuition (Falk 1992:202). People strongly tend to think probability is evenly distributed across as many unknowns as are present, whether it is or not (Fox and Levav, 2004:637).
A competing deeply rooted intuition at work in the Monty Hall problem is the belief that exposing information that is already known does not affect probabilities (Falk 1992:207). This intuition is the basis of solutions to the problem that assert the host's action of opening a door does not change the player's initial 1/3 chance of selecting the car. For the fully explicit problem this intuition leads to the correct numerical answer, 2/3 chance of winning the car by switching, but leads to the same solution for other variants where this answer is not correct (Falk 1992:207).
Another source of confusion is that the usual wording of the problem statement asks about the conditional probability of winning given which door is opened by the host, as opposed to the overall or unconditional probability. These are mathematically different questions and can have different answers depending on how the host chooses which door to open if the player's initial choice is the car (Morgan et al., 1991; Gillman 1992). For example, if the host opens Door 3 whenever possible then the probability of winning by switching for players initially choosing Door 1 is 2/3 overall, but only 1/2 if the host opens Door 3. In its usual form the problem statement does not specify this detail of the host's behavior, making the answer that switching wins the car with probability 2/3 mathematically unjustified. Many commonly presented solutions address the unconditional probability, ignoring which door the host opens; Morgan et al. call these "false solutions" (1991).
[edit] Aids to understanding
[edit] Why the probability is not 1/2
The most commonly voiced objection to the solution is that the past can be ignored when assessing the probability—that it is irrelevant which doors the player initially picks and the host opens. However, in the problem as originally presented, the player's initial choice does influence the host's available choices subsequently.
This difference can be demonstrated by contrasting the original problem with a variation that appeared in vos Savant's column in November 2006. In this version, Monty Hall forgets which door hides the car. He opens one of the doors at random and is relieved when a goat is revealed. Asked whether the contestant should switch, vos Savant correctly replied, "If the host is clueless, it makes no difference whether you stay or switch. If he knows, switch" (vos Savant, 2006).
In this version of the puzzle, the player has an equal chance of winning whether switching or not. Assuming the player picks Door 1 there are six possible outcomes that can occur, each with probability 1/6:
| Player picks Door 1 | ||||||
|---|---|---|---|---|---|---|
| Car behind Door 1 | Car behind Door 2 | Car behind Door 3 | ||||
| Host opens: | Door 2 | Door 3 | Door 2 | Door 3 | Door 2 | Door 3 |
| Host reveals: | Goat | Goat | Car | Goat | Goat | Car |
| Switching: | loses | loses | ? | wins | wins | ? |
In two cases above, the host reveals the car. What might happen in these cases is unknown—perhaps the contestant immediately wins or immediately loses. However, in the problem as stated, the host has revealed a goat, so only four of the six cases remain possible, and they are equally likely. In two of these four cases, switching results in a win, and in the other two, switching results in a loss. Staying with the original pick gives the same odds: a loss in two cases and a win in two others.
The player's probability of winning by switching increases to 2/3 in the original problem because in the two cases above where the host would reveal the car, he is forced to reveal the remaining goat instead. In the table below, these two cases are highlighted:
| Player picks Door 1 | ||||||
|---|---|---|---|---|---|---|
| Car behind Door 1 | Car behind Door 2 | Car behind Door 3 | ||||
| Host opens: | Door 2 | Door 3 | Door 3 | Door 3 | Door 2 | Door 2 |
| Host reveals: | Goat | Goat | Goat | Goat | Goat | Goat |
| Switching: | loses | loses | wins | wins | wins | wins |
This change in the host's behavior causes the car to be twice as likely to be behind the "third door", and is what makes switching twice as likely to win in the "host knows" variation of the problem.
[edit] Increasing the number of doors
It may be easier to appreciate the solution by considering the same problem with 1,000,000 doors instead of just three (vos Savant 1990). In this case there are 999,999 doors with goats behind them and one door with a prize. The player picks a door. The game host then opens 999,998 of the other doors revealing 999,998 goats—imagine the host starting with the first door and going down a line of 1,000,000 doors, opening each one, skipping over only the player's door and one other door. The host then offers the player the chance to switch to the only other unopened door. On average, in 999,999 out of 1,000,000 times the other door will contain the prize, as 999,999 out of 1,000,000 times the player first picked a door with a goat. A rational player should switch. Intuitively speaking, the player should ask how likely is it, that given a million doors, he or she managed to pick the right one.
Stibel et al. (2008) propose working memory demand is taxed during the Monty Hall problem and that this forces people to "collapse" their choices into two equally probable options. They report that when increasing the number of options to over 7 choices (7 doors) people tend to switch more often, however most still incorrectly judge the probability of success at 50/50.
[edit] Combining doors
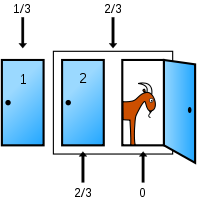
Instead of one door being opened and shown to be a losing door, an equivalent action is to combine the two unchosen doors into one since the player cannot, and will not, choose the opened door (Adams 1990; Devlin 2003; Williams 2004; Stibel et al., 2008). The player therefore has the choice of either sticking with the original choice of door with a 1/3 chance of winning the car, or choosing the sum of the contents of the two other doors with a 2/3 chance as shown.
The game assumptions play a role here—switching is equivalent to taking the combined contents if and only if the game host knows what is behind the doors, must open a door with a goat, and chooses between two losing doors randomly with equal probabilities.
The only difference between trading for both doors and the trade that is actually offered is whether the host opens one of the two doors. Opening one shows which of these doors the car must be behind if it is behind either. At least one of the two unpicked doors contains a goat, and the host is equally likely to open either of these doors so opening one gives the player no additional information; opening one does not change the 2/3 probability that the car is behind one of them (Devlin 2003).
[edit] Simulation
A simple way to demonstrate that a switching strategy really does win two out of three times on the average is to simulate the game with playing cards (Gardner 1959b; vos Savant 1996:8). Three cards from an ordinary deck are used to represent the three doors; one 'special' card such as the Ace of Spades should represent the door with the car, and ordinary cards, such as the two red twos, represent the goat doors.
The simulation, using the following procedure, can be repeated several times to simulate multiple rounds of the game. One card is dealt at random to the 'player', to represent the door the player picks initially. Then, looking at the remaining two cards at least one of which must be a red two, the 'host' discards a red two. If the card remaining in the host's hand is the Ace of Spades, this is recorded as a round where the player would have won by switching; if the host is holding a red two, the round is recorded as one where staying would have won.
By the law of large numbers, this experiment is likely to approximate the probability of winning, and running the experiment over enough rounds should not only verify that the player does win by switching two times out of three, but show why. After one card has been dealt to the player, it is already determined whether switching will win the round for the player; and two times out of three the Ace of Spades is in the host's hand.
If this is not convincing, the simulation can be done with the entire deck, dealing one card to the player and keeping the other 51 (Gardner 1959b; Adams 1990). In this variant the Ace of Spades goes to the host 51 times out of 52, and stays with the host no matter how many non-Ace cards are discarded.
[edit] Switching after elimination ensures change of object type
Another way of understanding the problem is recognizing that changing the choice after elimination is a guarantee of changing the type of the object chosen initially. i.e. if a goat was chosen initially the switch guarantees a car and vice versa. Since it is twice as likely that a goat would be chosen before elimination, the chances of winning a car after elimination are twice as likely if the player switched.
[edit] Variants
[edit] Other host behaviors
In some versions of the Monty Hall problem, the host's behavior is not fully specified. For example, the version published in Parade in 1990 did not specifically state that the host would always open another door, or always offer a choice to switch, or even never open the door revealing the car. Without specifying these rules, the player does not have enough information to conclude that switching will be successful two-thirds of the time (Mueser and Granberg, 1999). The table shows possible host behaviors and the impact on the success of switching.
| Possible host behaviors in unspecified problem | |
|---|---|
| Host behavior | Result |
| The host offers the option to switch only when the player's initial choice is the winning door (Tierney 1991). | Switching always yields a goat. |
| The host offers the option to switch only when the player has chosen incorrectly (Granberg 1996:185). | Switching always wins the car. |
| The host does not know what lies behind the doors, and opens one at random without revealing the car (Granberg and Brown, 1995:712). | Switching wins the car half of the time. |
| The host knows what lies behind the doors, and chooses at random which goat to reveal. He offers the option to switch only when the player's choice happens to differ from his. | Switching wins the car half of the time. |
| The host always reveals a goat and always offers a switch. If he has a choice, he chooses the leftmost goat with probability p (which may depend on the player's initial choice) and the rightmost door with probability q=1-p. (Morgan et al. 1991). | If the host opens the rightmost door, switching wins with probability 1/(1+q). |
| The host acts as noted in the specific version of the problem. | Switching wins the car two-thirds of the time. (Special case of the above with p=q=½) |
Determining the best strategy if the player does not know the host's behaviour is the type of problem studied in game theory. For example, the player may suspect the host is malicious and offers the chance to switch more often if the player has initially selected the car. In general, the answer to this sort of question depends on the specific assumptions made about the host's behaviour, and might range from "ignore the host completely" to 'toss a coin and switch if it comes up heads'.
[edit] N doors
D. L. Ferguson (1975 in a letter to Selvin cited in Selvin 1975b) suggests an N door generalization of the original problem in which the host opens p losing doors and then offers the player the opportunity to switch; in this variant switching wins with probability (N-1)/N(N-p-1). If the host opens even a single door the player is better off switching, but the advantage approaches zero as N grows large (Granberg 1996:188). At the other extreme, if the host opens all but one losing door the probability of winning by switching approaches 1.
Bapeswara Rao and Rao (1992) suggest a different N door version where the host opens a losing door different from the player's current pick and gives the player an opportunity to switch after each door is opened until only two doors remain. With four doors the optimal strategy is to pick once and switch only when two doors remain. With N doors this strategy wins with probability (N-1)/N and is asserted to be optimal.
This problem appears similar to the television show Deal or No Deal; however, with each selection the Deal or No Deal player is just as likely to open the winning box as a losing one. Monty, on the other hand, knows the contents and is forbidden from revealing the winner. Assuming the grand prize is still left with two boxes remaining, the Deal or No Deal player has a 50/50 chance that the initially selected box contains the grand prize.
[edit] Quantum version
A quantum version of the paradox illustrates some points about the relation between classical or non-quantum information and quantum information, as encoded in the states of quantum mechanical systems. The formulation is loosely based on Quantum game theory. The three doors are replaced by a quantum system allowing three alternatives; opening a door and looking behind it is translated as making a particular measurement. The rules can be stated in this language, and once again the choice for the player is to stick with the initial choice, or change to another "orthogonal" option. The latter strategy turns out to double the chances, just as in the classical case. However, if the show host has not randomized the position of the prize in a fully quantum mechanical way, the player can do even better, and can sometimes even win the prize with certainty (Flitney and Abbott 2002, D'Ariano et al. 2002).
[edit] History of the problem
The earliest of several probability puzzles related to the Monty Hall problem is Bertrand's box paradox, posed by Joseph Bertrand in 1889 in his Calcul des probabilités (Barbeau 1993). In this puzzle there are three boxes: a box containing two gold coins, a box with two silver coins, and a box with one of each. After choosing a box at random and withdrawing one coin at random that happens to be a gold coin, the question is what is the probability that the other coin is gold. As in the Monty Hall problem the intuitive answer is 1/2, but the probability is actually 2/3.
The Three Prisoners problem, published in Martin Gardner's Mathematical Games column in Scientific American in 1959 (1959a, 1959b), is isomorphic to the Monty Hall problem. This problem involves three condemned prisoners, a random one of whom has been secretly chosen to be pardoned. One of the prisoners begs the warden to tell him the name of one of the others who will be executed, arguing that this reveals no information about his own fate but increases his chances of being pardoned from 1/3 to 1/2. The warden obliges, (secretly) flipping a coin to decide which name to provide if the prisoner who is asking is the one being pardoned. The question is whether knowing the warden's answer changes the prisoner's chances of being pardoned. This problem is equivalent to the Monty Hall problem; the prisoner asking the question still has a 1/3 chance of being pardoned but his unnamed cohort has a 2/3 chance.
Steve Selvin posed the Monty Hall problem in a pair of letters to the American Statistician in 1975 (1975a, 1975b). The first letter presented the problem in a version close to its presentation in Parade 15 years later. The second appears to be the first use of the term "Monty Hall problem". The problem is actually an extrapolation from the game show. Monty Hall did open a wrong door to build excitement, but offered a known lesser prize—such as $100 cash—rather than a choice to switch doors. As Monty Hall wrote to Selvin:
And if you ever get on my show, the rules hold fast for you—no trading boxes after the selection. (Hall 1975)
A version of the problem very similar to the one that appeared three years later in Parade was published in 1987 in the Puzzles section of The Journal of Economic Perspectives (Nalebuff 1987).
Phillip Martin's article in a 1989 issue of Bridge Today magazine titled "The Monty Hall Trap" (Martin 1989) presented Selvin's problem, with the correct solution, as an example of how one can fall into the trap of treating non-random information as if it were random. Martin then gives examples in the game of bridge where players commonly miscalculate the odds by falling into the same trap, such as the Principle of Restricted Choice. Given the controversy that would arise over this problem a year later, Martin showed a lack of prescience when he stated, "Here [in the Monty Hall problem] the trap is easy to spot. But the trap can crop up more subtly in a bridge setting."
A restated version of Selvin's problem appeared in Marilyn vos Savant's Ask Marilyn question-and-answer column of Parade in September 1990 (vos Savant 1990). Though vos Savant gave the correct answer that switching would win two-thirds of the time, she estimates the magazine received 10,000 letters including close to 1,000 signed by Ph.D.s, many on letterheads of mathematics and science departments, declaring that her solution was wrong (Tierney 1991). Due to the overwhelming response, Parade published an unprecedented four columns on the problem (vos Savant 1996:xv). As a result of the publicity the problem earned the alternative name Marilyn and the Goats.
In November 1990, an equally contentious discussion of vos Savant's article took place in Cecil Adams's column The Straight Dope (Adams 1990). Adams initially answered, incorrectly, that the chances for the two remaining doors must each be one in two. After a reader wrote in to correct the mathematics of Adams' analysis, Adams agreed that mathematically, he had been wrong, but said that the Parade version left critical constraints unstated, and without those constraints, the chances of winning by switching were not necessarily 2/3. Numerous readers, however, wrote in to claim that Adams had been "right the first time" and that the correct chances were one in two.
The Parade column and its response received considerable attention in the press, including a front page story in the New York Times (Tierney 1991) in which Monty Hall himself was interviewed. He appeared to understand the problem quite well, giving the reporter a demo with car keys and explaining how actual game play on Let's Make a Deal differed from the rules of the puzzle.
Over 40 papers have been published about this problem in academic journals and the popular press (Mueser and Granberg 1999).
The problem continues to resurface outside of academia. The syndicated NPR program Car Talk featured it as one of their weekly "Puzzlers," and the answer they featured was quite clearly explained as the correct one (Magliozzi and Magliozzi, 1998). An account of mathematician Paul Erdos's first encounter of the problem can be found in The Man Who Loved Only Numbers—like many others, he initially got it wrong. The problem is discussed, from the perspective of a boy with Asperger syndrome, in The Curious Incident of the Dog in the Night-time, a 2003 novel by Mark Haddon. The problem is also addressed in a lecture by the character Charlie Eppes in an episode of the CBS drama NUMB3RS (Episode 1.13) and in Derren Brown's 2006 book Tricks Of The Mind. Penn Jillette explained the Monty Hall Problem on the "Luck" episode of Bob Dylan's Theme Time Radio Hour radio series. The Monty Hall problem appears in the film 21 (Bloch 2008). Economist M. Keith Chen identified a potential flaw in hundreds of experiments related to cognitive dissonance that use an analysis with issues similar to those involved in the Monty Hall problem (Tierney 2008).
[edit] Bayesian analysis
An analysis of the problem using the formalism of Bayesian probability theory (Gill 2002) makes explicit the role of the assumptions underlying the problem.
In Bayesian terms, a probability  is a number in
is a number in ![[0, 1]\,](http://upload.wikimedia.org/math/d/0/9/d09694b77d8a3a03f6879fa37f09d0b0.png) associated to a proposition
associated to a proposition  . The number expresses a degree of belief in the truth of
. The number expresses a degree of belief in the truth of  , subject to whatever background information
, subject to whatever background information  happens to be known.
happens to be known.
For this problem the background is provided by the rules of the game, and the propositions of interest are:
 : The car is behind Door i, for i equal to 1, 2 or 3.
: The car is behind Door i, for i equal to 1, 2 or 3.
 : The host opens Door j after the player has picked Door i, for i and j equal to 1, 2 or 3.
: The host opens Door j after the player has picked Door i, for i and j equal to 1, 2 or 3.
For example,  denotes the proposition the car is behind Door 1, and
denotes the proposition the car is behind Door 1, and 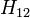 denotes the proposition the host opens Door 2 after the player has picked Door 1.
denotes the proposition the host opens Door 2 after the player has picked Door 1.
The assumptions underlying the common interpretation of the Monty Hall puzzle are then formally stated as follows.
First, the car can be behind any door, and all doors are a priori equally likely to hide the car. In this context a priori means before the game is played, or before seeing the goat. Hence, the prior probability of a proposition  is:
is:
Second, the host will always open a door that has no car behind it, chosen from among the two not picked by the player. If two such doors are available, each one is equally likely to be opened. This rule determines the conditional probability of a proposition  subject to where the car is — i.e., conditioned on a proposition
subject to where the car is — i.e., conditioned on a proposition  Specifically, it is:
Specifically, it is:
-


if i = j, (the host cannot open the door picked by the player) 
if j = k, (the host cannot open a door with a car behind it) 
if i = k, (the two doors with no car are equally likely to be opened) 
if i 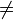 k and j
k and j 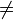 k, (there is only one door available to open)
k, (there is only one door available to open)
The problem can now be solved by scoring each strategy with its associated posterior probability of winning, that is with its probability subject to the host's opening of one of the doors. Without loss of generality, assume, by re-numbering the doors if necessary, that the player picks Door 1, and that the host then opens Door 3, revealing a goat. In other words, the host makes proposition  true.
true.
The posterior probability of winning by not switching doors, subject to the game rules and  , is then
, is then  . Using Bayes' theorem this is expressed as:
. Using Bayes' theorem this is expressed as:
By the assumptions stated above, the numerator of the right-hand side is:
The normalizing constant at the denominator can be evaluated by expanding it using the definitions of marginal probability and conditional probability:
Dividing the numerator by the normalizing constant yields:
Note that this is equal to the prior probability of the car's being behind the initially chosen door, meaning that the host's action has not contributed any novel information with regard to this eventuality. In fact, the following argument shows that the effect of the host's action consists entirely of redistributing the probabilities for the car's being behind either of the other two doors.
The probability of winning by switching the selection to Door 2, 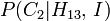 , can be evaluated by requiring that the posterior probabilities of all the
, can be evaluated by requiring that the posterior probabilities of all the  propositions add to 1. That is:
propositions add to 1. That is:
There is no car behind Door 3, since the host opened it, so the last term must be zero. This can be proven using Bayes' theorem and the previous results:
Hence:
This shows that the winning strategy is to switch the selection to Door 2. It also makes clear that the host's showing of the goat behind Door 3 has the effect of transferring the 1/3 of winning probability a-priori associated with that door to the remaining unselected and unopened one, thus making it the most likely winning choice.
[edit] See also
[edit] Similar problems
- Bertrand's box paradox (also known as the Three cards problem)
- Boy or Girl paradox
- Three Prisoners problem
- Two envelopes problem
[edit] References
- Adams, Cecil (1990)."On 'Let's Make a Deal,' you pick Door #1. Monty opens Door #2—no prize. Do you stay with Door #1 or switch to #3?", The Straight Dope, (November 2, 1990). Retrieved July 25, 2005.
- Bapeswara Rao, V. V. and Rao, M. Bhaskara (1992). "A three-door game show and some of its variants". The Mathematical Scientist 17(2): 89–94.
- Barbeau, Edward (1993). "Fallacies, Flaws, and Flimflam: The problem of the Car and Goats". The College Mathematics Journal 24(2): 149-154.
- Barbeau, Edward (2000). Mathematical Fallacies, Flaws and Flimflam. The Mathematical Association of America. ISBN 0-8838-5529-1.
- Bloch, Andy (2008). "21 - The Movie (my review)". http://www.andybloch.com/gl/pub/article.php?story=2008031308241327. Retrieved on 2008-05-05.
- Chun, Young H. (1991). "Game Show Problem," OR/MS Today 18(3): 9.
- D'Ariano, G.M et al. (2002). "The Quantum Monty Hall Problem" (PDF). Los Alamos National Laboratory, (February 21, 2002). Retrieved January 15, 2007.
- Devlin, Keith (July – August 2003). "Devlin's Angle: Monty Hall". The Mathematical Association of America. http://www.maa.org/devlin/devlin_07_03.html. Retrieved on 2008-04-25.
- Falk, Ruma (1992). "A closer look at the probabilities of the notorious three prisoners," Cognition 43: 197–223.
- Flitney, Adrian P. and Abbott, Derek (2002). "Quantum version of the Monty Hall problem," Physical Review A, 65, Art. No. 062318, 2002.
- Fox, Craig R. and Levav, Jonathan (2004). "Partition-Edit-Count: Naive Extensional Reasoning in Judgment of Conditional Probability," Journal of Experimental Psychology: General 133(4): 626-642.
- Gardner, Martin (1959a). "Mathematical Games" column, Scientific American, October 1959, pp. 180–182. Reprinted in The Second Scientific American Book of Mathematical Puzzles and Diversions.
- Gardner, Martin (1959b). "Mathematical Games" column, Scientific American, November 1959, p. 188.
- Gill, Jeff (2002). Bayesian Methods, pp. 8–10. CRC Press. ISBN 1-5848-8288-3.
- Gillman, Leonard (1992). "The Car and the Goats," American Mathematical Monthly 99: 3–7.
- Granberg, Donald (1996). "To Switch or Not to Switch". Appendix to vos Savant, Marilyn, The Power of Logical Thinking. St. Martin's Press. ISBN 0-612-30463-3.
- Granberg, Donald and Brown, Thad A. (1995). "The Monty Hall Dilemma," Personality and Social Psychology Bulletin 21(7): 711-729.
- Grinstead, Charles M. and Snell, J. Laurie (2006-07-04) (PDF). Grinstead and Snell’s Introduction to Probability. Online version of Introduction to Probability, 2nd edition, published by the American Mathematical Society, Copyright (C) 2003 Charles M. Grinstead and J. Laurie Snell.. http://www.math.dartmouth.edu/~prob/prob/prob.pdf. Retrieved on 2008-04-02.
- Hall, Monty (1975). The Monty Hall Problem. LetsMakeADeal.com. Includes May 12, 1975 letter to Steve Selvin. Retrieved January 15, 2007.
- Krauss, Stefan and Wang, X. T. (2003). "The Psychology of the Monty Hall Problem: Discovering Psychological Mechanisms for Solving a Tenacious Brain Teaser," Journal of Experimental Psychology: General 132(1). Retrieved from http://www.usd.edu/~xtwang/Papers/MontyHallPaper.pdf March 30, 2008.
- Mack, Donald R. (1992). The Unofficial IEEE Brainbuster Gamebook. Wiley-IEEE. p. 76. ISBN 9780780304239. http://books.google.com/books?id=hcy9mQp83dEC&pg=PA18&dq=%22monty+hall+problem%22&lr=&as_drrb_is=b&as_minm_is=0&as_miny_is=&as_maxm_is=0&as_maxy_is=1995&as_brr=3&as_pt=ALLTYPES&ei=MqDVSYDkHpeSkASZvbi-Bg#PPA76,M1.
- Magliozzi, Tom; Magliozzi, Ray (1998). Haircut in Horse Town: & Other Great Car Talk Puzzlers. Diane Pub Co.. ISBN 0-7567-6423-8.
- Martin, Phillip (1989). "The Monty Hall Trap", Bridge Today, May–June 1989. Reprinted in Granovetter, Pamela and Matthew, ed. (1993), For Experts Only, Granovetter Books.
- Morgan, J. P., Chaganty, N. R., Dahiya, R. C., & Doviak, M. J. (1991). "Let's make a deal: The player's dilemma," American Statistician 45: 284-287.
- Mueser, Peter R. and Granberg, Donald (May 1999). "The Monty Hall Dilemma Revisited: Understanding the Interaction of Problem Definition and Decision Making", University of Missouri Working Paper 99-06. Retrieved July 5, 2005.
- Nalebuff, Barry (1987). "Puzzles: Choose a Curtain, Duel-ity, Two Point Conversions, and More," Journal of Economic Perspectives 1(2): 157-163 (Autumn, 1987).
- Selvin, Steve (1975a). "A problem in probability" (letter to the editor). American Statistician 29(1): 67 (February 1975).
- Selvin, Steve (1975b). "On the Monty Hall problem" (letter to the editor). American Statistician 29(3): 134 (August 1975).
- Stibel, Jeffrey, Dror, Itiel, & Ben-Zeev, Talia (2008). "The Collapsing Choice Theory: Dissociating Choice and Judgment in Decision Making," Theory and Decision. Full paper can be found at http://users.ecs.soton.ac.uk/id/TD%20choice%20and%20judgment.pdf.
- Tierney, John (1991). "Behind Monty Hall's Doors: Puzzle, Debate and Answer?", The New York Times, 1991-07-21. Retrieved on 2008-01-18.
- Tierney, John (2008). "And Behind Door No. 1, a Fatal Flaw", The New York Times, 2008-04-08. Retrieved on 2008-04-08.
- vos Savant, Marilyn (1990). "Ask Marilyn" column, Parade Magazine p. 16 (9 September 1990).
- vos Savant, Marilyn (1996). The Power of Logical Thinking. St. Martin's Press. ISBN 0-612-30463-3. http://books.google.com/books?id=pgQQv8W_IgIC&pg=PA5&dq=%22monty+hall+paradox%22+inauthor:savant&lr=&as_brr=0&as_pt=ALLTYPES&ei=aETYSZDDDoWqlQSIgMHlAg#PPA6,M1.
- vos Savant, Marilyn (2006). "Ask Marilyn" column, Parade Magazine p. 6 (26 November 2006).
- Jack D. Schwager (1994). The New Market Wizards. Harper Collins. p. 397. ISBN 9780887306679. http://books.google.com/books?id=Ezz_gZ-bRzwC&pg=PA397&dq=three-doors+monty-hall&lr=&as_drrb_is=b&as_minm_is=0&as_miny_is=&as_maxm_is=12&as_maxy_is=1994&as_brr=3&as_pt=ALLTYPES&ei=qRTYSZOjLIzOkATFw_HwAg.
- Williams, Richard (2004). "Appendix D: The Monty Hall Controversy" (PDF). Course notes for Sociology Graduate Statistics I. http://www.nd.edu/~rwilliam/stats1/appendices/xappxd.pdf. Retrieved on 2008-04-25.
- Wheeler, Ward C. (1991). "Congruence Among Data Sets: A Bayesian Approach". in Michael M. Miyamoto and Joel Cracraft. Phylogenetic analysis of DNA sequences. Oxford University Press US. p. 335. ISBN 9780195066982. http://books.google.com/books?id=1wqvNgz58JQC&pg=PA335&dq=%22monty+hall%22+unchanged+switch&lr=&as_brr=3&as_pt=ALLTYPES&ei=FsnSSYeXFo7skwT64ezkCQ.
- Whitaker, Craig F. (1990). [Letter]. "Ask Marilyn" column, Parade Magazine p. 16 (9 September 1990).
[edit] External links
| The Wikibook Algorithm implementation has a page on the topic of |
| Wikimedia Commons has media related to: Monty Hall problem |
- The Monty Hall Problem at letsmakeadeal.com
- The Game Show Problem–the original question and responses on Marilyn vos Savant's web site
- Monty Hall at the Open Directory Project
- "Monty Hall Paradox" by Matthew R. McDougal, The Wolfram Demonstrations Project (simulation)
- The Monty Hall Problem at The New York Times (simulation)