Secretary problem
From Wikipedia, the free encyclopedia
The secretary problem (more precisely, the classical secretary problem) is an optimal stopping problem that has been studied extensively in the fields of applied probability, statistics, and decision theory. It is also known as the marriage problem, the sultan's dowry problem, the fussy suitor problem, the googol game, and the best choice problem. The solution is sometimes called the 37% rule. The problem can be stated as follows:
- There is a single secretarial position to fill.
- There are n applicants for the position, and the value of n is known.
- The applicants can be ranked from best to worst with no ties.
- The applicants are interviewed sequentially in a random order, with each order being equally likely.
- After each interview, the applicant is accepted or rejected.
- The decision to accept or reject an applicant can be based only on the relative ranks of the applicants interviewed so far.
- Rejected applicants cannot be recalled.
- The object is to select the best applicant. The payoff is 1 for the best applicant and zero otherwise.
Terminology: A candidate is an applicant who, when interviewed, is better than all the applicants interviewed previously. Skip is used to mean "interview and reject".
Clearly, since the objective in the problem is to select the single best applicant, only candidates will be considered for acceptance. One reason why the secretary problem has received so much attention is that the optimal policy for the problem (the stopping rule) has a surprising feature. Specifically, for large n the optimal policy is to interview and reject the first n/e applicants (where e is the base of the natural logarithm) and then to accept the next who is better than these interviewed candidates. As n gets larger, the probability of selecting the best applicant from the pool goes to 1/e, which is around 37%. Whether one is searching through 100 or 100,000,000 applicants, the optimal policy will select the single best one about 37% of the time.
Contents |
[edit] Deriving the optimal policy
The optimal policy for the problem is a stopping rule. Under it, the interviewer should skip the first r − 1 applicants, and then take the next applicant who is a candidate (i.e., who has the best relative ranking of those interviewed up to that point). It can be shown, that the optimal strategy lies in this class of strategies. For an arbitrary cutoff r, the probability that the best applicant is selected is
Letting n tend to infinity, writing x as the limit of r/n, using t for j/n and dt for 1/n, the sum can be approximated by the integral
Taking the derivative of P(r) with respect to x, setting it to 0, and solving for x, we find that the optimal x is equal to 1/e. Thus, the optimal cutoff tends to n/e as n increases, and the best applicant is selected with probability 1/e.
For small values of n, the optimal r can also be obtained by standard dynamic programming methods. The optimal thresholds r and probability of selecting the best alternative P for several values of n are shown in the following table.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| r | 1 | 1 | 2 | 2 | 3 | 3 | 3 | 4 | 4 |
| P | 1.000 | 0.500 | 0.500 | 0.458 | 0.433 | 0.428 | 0.414 | 0.410 | 0.406 |
Note that the probability of selecting the best alternative in the classical secretary problem converges toward  .
.
[edit] Alternative solution
This problem and several modifications can be solved (including the proof of optimality) in a straightforward manner by the Odds algorithm (2000) which also allows for other applications. Modifications for the secretary problem which can be solved by this algorithm include random availabilties of applicants, more general hypotheses for applicants to be of interest to the decision maker, group interviews for applicants, as well as certain models for a random number of applicants. None of these modifications are treated in this article.
[edit] Unknown number of applicants
A major drawback for applications of the solution of the classical secretary problem is that the number of applicants n must be known in advance. One way to overcome this problem is to suppose that the number of applicants is a random variable N with a known distribution of  (Presman and Sonin, 1972). For this model, the optimal solution is in general much harder, however. Moreover, the optimal success probability is now no longer around 1/e. Indeed, it is intuitive that there should be a price to pay for not knowing the number of applicants. However, in this model the price is high. Depending on the choice of the distribution of N the optimal win probability is typically much lower than 1/e, and may even approach zero. This reduces the interest of this model for applications. Looking for ways to cope with this new problem finally lead to the following approach and result.
(Presman and Sonin, 1972). For this model, the optimal solution is in general much harder, however. Moreover, the optimal success probability is now no longer around 1/e. Indeed, it is intuitive that there should be a price to pay for not knowing the number of applicants. However, in this model the price is high. Depending on the choice of the distribution of N the optimal win probability is typically much lower than 1/e, and may even approach zero. This reduces the interest of this model for applications. Looking for ways to cope with this new problem finally lead to the following approach and result.
[edit] 1/e-law of best choice
The essence of the model is based on the idea that real-world problems pose themselves in real time and that it is easier to estimate times in which specific events (arrivals of applicants) should occur more likely (if they do) than to estimate the distribution of the number of specific events which will occur. This idea lead to the following approach, the so-called Unified approach(1984):
The model: An applicant must be selected on some time interval [0,T] from an unknown number N of rankable applicants. The goal is to maximize the probability of selecting online the best under the hypothesis that all arrival orders of different ranks are equally likely. Suppose that all applicants have independently of each other the same arrival time density f on [0,T] and let F denote the corresponding arrival time distribution function, that is
 ,
,  .
.
1/e-law: Let τ be such that F(τ) = 1 / e. Consider the strategy to wait and observe all applicants up to time τ and then to select, if possible, the first candidate after time τ which is better than all preceding ones. Then this strategy, called 1/e-strategy, has the following properties:
The 1/e-strategy
- (i) yields for all N a success probability of at least 1/e,
- (ii) is the unique strategy guaranteeing this lower success probability bound 1/e, and the bound is optimal,
- (iii) selects, if there is at least one applicant, none at all with probability exactly 1/e.
When the 1/e-law was discovered in 1984 it came as a surprise. The reason was that a value of about 1/e had been considered before as being out of reach in a model for unknown N, whereas now this value was achieved as a lower bound, and this in a model with arguably weaker hypotheses (see e.g. Math. Reviews 85:m).
This law is sometimes confused with the solution for the secretary problem because of the similar role of the number 1/e. Note however that in the 1/e-law, this role is stronger and more general. The result is also stronger, since it holds for an unknown number of applicants and since the model is more tractable for applications.
[edit] Heuristic performance
The remainder of the article deals again with the secretary problem for a known number of applicants.
Stein, Seale, and Rapoport (2003) derived the expected success probabilities for several psychologically plausible heuristics that might be employed in the secretary problem. The heuristics they examined were:
- The cutoff rule (CR): Do not accept any of the first y applicants; thereafter, select the first encountered candidate (i.e., an applicant with relative rank 1). This rule has as a special case the optimal policy for the CSP for which y = r.
- Candidate count rule (CCR): Select the y encountered candidate. Note, that this rule does not necessarily skip any applicants; it only considers how many candidates have been observed, not how deep the decision maker is in the applicant sequence.
- Successive non-candidate rule (SNCR): Select the first encountered candidate after observing y non-candidates (i.e., applicants with relative rank > 1).
Note that each heuristic has a single parameter y. The figure (shown on right) displays the expected success probabilities for each heuristic as a function of y for problems with n = 80.
[edit] Cardinal payoff variant
Finding the single best applicant might seem like a rather strict objective. One can imagine that the interviewer would rather hire a higher-valued applicant than a lower-valued one, and not only be concerned with getting the best. That is, she will derive some value from selecting an applicant that is not necessarily the best, and the value she derives is increasing in the value of the one she selects.
To model this problem, suppose that the n applicants have "true" values that are random variables X drawn i.i.d. from a uniform distribution on [0, 1]. Similar to the classical problem described above, the interviewer only observes whether each applicant is the best so far (a candidate), must accept or reject each on the spot, and must accept the last one if he is reached. (To be clear, the interviewer does not learn the actual relative rank of each applicant. She learns only whether the applicant has relative rank 1.) However, in this version her payoff is given by the true value of the selected applicant. For example, if she selects an applicant whose true value is 0.8, then she will earn 0.8. The interviewer's objective is to maximize the expected value of the selected applicant.
Since the applicant's values are i.i.d. draws from a uniform distribution on [0, 1], the expected value of the tth applicant given that  is given by
is given by
As in the classical problem, the optimal policy is given by a threshold, which for this problem we will denote by c, at which the interviewer should begin accepting candidates. Bearden (2006) showed that c is either  or
or  . This follows from the fact that given a problem with n applicants, the expected payoff for some arbitrary threshold 1 ≤ c ≤ n is
. This follows from the fact that given a problem with n applicants, the expected payoff for some arbitrary threshold 1 ≤ c ≤ n is
Differentiating Vn(c) with respect to c, one gets
Since  for all permissible values of c, we find that V is maximized at
for all permissible values of c, we find that V is maximized at  . Since V is convex in c, the optimal integer-valued threshold must be either
. Since V is convex in c, the optimal integer-valued threshold must be either  or
or  . Thus, for most values of n the interviewer will begin accepting applicants sooner in the cardinal payoff version than in the classical version where the objective is to select the single best applicant. Note that this is not an asymptotic result: It holds for all n.
. Thus, for most values of n the interviewer will begin accepting applicants sooner in the cardinal payoff version than in the classical version where the objective is to select the single best applicant. Note that this is not an asymptotic result: It holds for all n.
[edit] Experimental studies
Psychologists and experimental economists have studied the decision behavior of actual people in secretary problems [1]. In large part, this work has shown that people tend to stop searching too soon. This may be explained, at least in part, by the cost of evaluating candidates. Extrapolating to real world settings, this might suggest that people do not search enough whenever they are faced with problems where the decision alternatives are encountered sequentially. For example, when trying to decide at which gas station to stop for gas, people might not search enough before stopping. If true, then they would tend to pay more for gas than they might had they searched longer. The same may be true when people search online for airline tickets, say. Experimental research on problems such as the secretary problem is sometimes referred to as behavioral operations research.
[edit] Origin of the problem
The secretary problem was apparently introduced in 1949 by Merrill M. Flood, who called it the fiancée problem in a lecture he gave that year. He referred to it several times during the 1950s, for example in a conference talk at Purdue on 9 May 1958, and it eventually became widely known in the folklore although nothing was published at the time. In 1958 he sent a letter to Leonard Gilman, with copies to a dozen friends including S. Karlin and J. Robbins, outlining a proof of the optimum strategy, with an appendix by R. Palermo who proved that all strategies are dominated by a strategy of the form "reject the first p unconditionally, then accept the next candidate". (See Flood (1958).)
The first publication was apparently by Martin Gardner in Scientific American, February 1960. He had heard about it from John H. Fox, Jr., and L. Gerald Marnie, who had independently come up with an equivalent problem in 1958; they called it the "game of Googol". Fox and Marnie did not know the optimum solution; Gardner asked for advice from Leo Moser, who (together with J. R. Pounder) provided a correct analysis for publication in the magazine. Soon afterwards, several mathematicians wrote to Gardner to tell him about the equivalent problem they had heard via the grapevine, all of which can most likely be traced to Flood's original work.
The 1/e-law is due to F. Thomas Bruss (1984)
A 1989 paper by T. S. Ferguson has an extensive bibliography, and points out that a similar (but different) problem had been considered by Arthur Cayley in 1875 and even by Johannes Kepler long before that.
[edit] See also
[edit] References
- J. N. Bearden. "A new secretary problem with rank-based selection and cardinal payoffs." Journal of Mathematical Psychology, volume 50, pp.58-59. 2006.
- J. N. Bearden, R. O. Murphy, Rapoport, A. "A multi-attribute extension of the secretary problem: Theory and experiments." Journal of Mathematical Psychology, volume 49, pp.410-425. 2005.
- J. N. Bearden, A. Rapoport, R. O. Murphy. "Sequential observation and selection with rank-dependent payoffs: An experimental test." Management Science, volume 52, pp. 1437-1449. 2006.
- F. Thomas Bruss A unified Approach to a Class of Best Choice problems with an Unknown Number of Options, Annals of Probability, Vol.12, pp. 882-891 (1984)
- F. Thomas Bruss Sum the odds to one and stop, Annals of Probability, Vol. 28. 1384-1391. (2000)
- T. S. Ferguson.[2] "Who solved the secretary problem?" Statistical science, volume 4, pp.282-296. 1989.
- P. R. Freeman. "The secretary problem and its extensions: A review." International Statistical Review / Revue Internationale de Statistique, volume 51, pp. 189-206. 1983.
- D. A. Seale, A. Rapoport. "Sequential decision making with relative ranks: An experimental investigation of the 'secretary problem.'" Organizational Behavior and Human Decision Processes, volume 69, pp.221-236. 1997.
- W. E. Stein, D. A. Seale, A. Rapoport. "Analysis of heuristic solutions to the best choice problem." European Journal of Operational Research, volume 151, pp.140-152.
- Merrill R. Flood, letter written in 1958, a copy of which can be found in the Martin Gardner papers at Stanford University Archives, series 1, box 5, folder 19.
- Martin Gardner, New Mathematical Diversions from Scientific American. Simon and Schuster, 1966, Chapter 3, Problem 3 [reprints his original column published in February 1960 with additional comments].
- The mating mind: how sexual choice shaped the evolution of human nature, Geoffrey F. Miller, Anchor Books, 2001, ISBN 038549517X, 9780385495172
- Framing Our Thoughts: Ecological Rationality as Evolutionary Psychology's Answer to the Frame Problem, Timothy Ketelaar and Peter M. Todd, Chapter 5 of Conceptual Challenges in Evolutionary Psychology, p. 187.
[edit] Notes
- ^ Bearden, Murphy, and Rapoport, 2006; Bearden, Rapoport, and Murphy, 2006; Seale and Rapoport, 1997
- ^ A mathematics professor at UCLA and the father of Chris "Jesus" Ferguson, the professional poker player
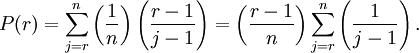



![V_{n}(c)=\sum_{t=c}^{n-1}\left[\prod_{s=c}^{t-1}\left(\frac{s-1}{s}\right)\right]\left(\frac{1}{t+1}\right)
+\left[\prod_{s=c}^{n-1}\left(\frac{s-1}{s}\right)\right]\frac{1}{2}={\frac {2cn-{c}^{2}+c-n}{2cn}}.](http://upload.wikimedia.org/math/c/8/5/c854aae43537082746b2f028c33a7999.png)


