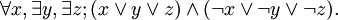Boolean satisfiability problem

From Wikipedia, the free encyclopedia

Jump to: navigation, search
"3SAT" redirects here. For the television network, see 3sat.

Satisfiability is the problem of determining if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE. Equally important is to determine whether no such assignments exist, which would imply that the function expressed by the formula is identically FALSE for all possible variable assignments. In this latter case, we would say that the function is unsatisfiable; otherwise it is satisfiable. To emphasize the binary nature of this problem, it is frequently referred to as Boolean or propositional satisfiability. The shorthand "SAT" is also commonly used to denote it, with the implicit understanding that the function and its variables are all binary-valued.

Contents

[edit] Basic definitions, terminology and applications

In complexity theory, the Boolean satisfiability problem (SAT) is a decision problem, whose instance is a Boolean expression written using only AND, OR, NOT, variables, and parentheses. The question is: given the expression, is there some assignment of TRUE and FALSE values to the variables that will make the entire expression true? A formula of propositional logic is said to be satisfiable if logical values can be assigned to its variables in a way that makes the formula true. The boolean satisfiability problem is NP-complete. The propositional satisfiability problem (PSAT), which decides whether a given propositional formula is satisfiable, is of central importance in various areas of computer science, including theoretical computer science, algorithmics, artificial intelligence, hardware design, electronic design automation, and verification.

The problem can be significantly restricted while still remaining NP-complete. By applying De Morgan's laws, we can assume that NOT operators are only applied directly to variables, not expressions; we refer to either a variable or its negation as a literal. For example, both x1 and not(x2) are literals, the first a positive literal and the second a negative literal. If we OR together a group of literals, we get a clause, such as (x1 or not(x2)). Finally, let us consider formulae that are a conjunction (AND) of clauses - this is the conjunctive normal form (CNF). Determining whether a formula in this form is satisfiable is still NP-complete, even if each clause is limited to at most three literals. This last problem is called 3SAT, 3CNFSAT, or 3-satisfiability.

On the other hand, if we restrict each clause to at most two literals, the resulting problem, 2SAT, is NL-complete. Alternately, if every clause must be a Horn clause, containing at most one positive literal, the resulting problem, Horn-satisfiability, is P-complete.

The Cook–Levin theorem proves that the Boolean satisfiability problem is NP-complete, and in fact, this was the first decision problem proved to be NP-complete. However, beyond this theoretical significance, efficient and scalable algorithms for SAT that were developed over the last decade have contributed to dramatic advances in our ability to automatically solve problem instances involving tens of thousands of variables and millions of constraints. Examples of such problems in Electronic Design Automation (EDA) include combinational equivalence checking, model checking, formal verification of pipelined microprocessors, automatic test pattern generation, routing of FPGAs, and so on. In fact, an SAT-solving engine is now considered to be an essential component in the EDA toolbox and all EDA vendors provide such a capability (usually behind the scenes.)

[edit] Complexity and restricted versions

[edit] NP-completeness

SAT was the first known NP-complete problem, as proved by Stephen Cook in 1971 (see Cook's theorem for the proof). Until that time, the concept of an NP-complete problem did not even exist. The problem remains NP-complete even if all expressions are written in conjunctive normal form with 3 variables per clause (3-CNF), yielding the 3SAT problem. This means the expression has the form:

(x11 OR x12 OR x13) AND
(x21 OR x22 OR x23) AND
(x31 OR x32 OR x33) AND ...

where each x is a variable or a negation of a variable, and each variable can appear multiple times in the expression.

A useful property of Cook's reduction is that it preserves the number of accepting answers. For example, if a graph has 17 valid 3-colorings, the SAT formula produced by the reduction will have 17 satisfying assignments.

NP-completeness only refers to the run-time of the worst case instances. Many of the instances that occur in practical applications can be solved much more quickly. See runtime behavior below.

SAT is easier if the formulas are restricted to those in disjunctive normal form, that is, they are disjunction (OR) of terms, where each term is a conjunction (AND) of literals (possibly negated variables). Such a formula is indeed satisfiable if and only if at least one of its terms is satisfiable, and a term is satisfiable if and only if it does not contain both x and NOT x for some variable x. This can be checked in polynomial time.

[edit] 2-satisfiability

Main article: 2-satisfiability

SAT is also easier if the number of literals in a clause is limited to 2, in which case the problem is called 2SAT. This problem can also be solved in polynomial time, and in fact is complete for the class NL. Similarly, if we limit the number of literals per clause to 2 and change the AND operations to XOR operations, the result is exclusive-or 2-satisfiability, a problem complete for SL = L.

One of the most important restrictions of SAT is HORNSAT, where the formula is a conjunction of Horn clauses. This problem is solved by the polynomial-time Horn-satisfiability algorithm, and is in fact P-complete. It can be seen as P's version of the Boolean satisfiability problem.

Provided that the complexity classes P and NP are not equal, none of these restrictions are NP-complete, unlike SAT. The assumption that P and NP are not equal is not currently proven.

[edit] 3-satisfiability

3-satisfiability is a special case of k-satisfiability (k-SAT) or simply satisfiability (SAT), when each clause contains exactly k = 3 literals. It was one of Karp's 21 NP-complete problems.

Here is an example, where ¬ indicates NOT:

E = (x1 or ¬x2 or ¬x3) and (x1 or x2 or x4)

E has two clauses (denoted by parentheses), four literals (x1, x2, x3, x4), and k=3 (three literals per clause).

To solve this instance of the decision problem we must determine whether there is a truth value (TRUE or FALSE) we can assign to each of the literals (x1 through x4) such that the entire expression is TRUE. In this instance, there is such an assignment (x1 = TRUE, x2 = TRUE, x3=TRUE, x4=TRUE), so the answer to this instance is YES. This is one of many possible assignments, with for instance, any set of assignments including x1 = TRUE being sufficient. If there were no such assignment(s), the answer would be NO.

Since k-SAT (the general case) reduces to 3-SAT, and 3-SAT can be proven to be NP-complete, it can be used to prove that other problems are also NP-complete. This is done by showing how a solution to another problem could be used to solve 3-SAT. An example of a problem where this method has been used is "Clique". It's often easier to use reductions from 3-SAT than SAT to problems that researchers are attempting to prove NP-complete.

3-SAT can be further restricted to One-in-three 3SAT, where we ask if exactly one of the variables in each clause is true, rather than at least one. One-in-three 3SAT remains NP-complete.

[edit] Horn-satisfiability

Main article: Horn-satisfiability

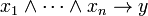A clause is Horn if it contains at most one positive literal. Such clauses are of interest because they are able to express implication of one variable from a set of other variables. Indeed, one such clause \neg x_1 \vee \cdots \vee \neg x_n \vee y can be rewritten as x_1 \wedge \cdots \wedge x_n \rightarrow y, that is, if 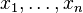x_1,\ldots,x_n are all true, then y needs to be true as well.

The problem of deciding whether a set of Horn clauses is satisfiable is in P. This problem can indeed be solved by a single step of the Unit propagation, which produces the single minimal (w.r.t. the set of literal assigned to true) model of the set of Horn clauses.

A generalization of the class of Horn formulae is that of renamable-Horn formulae, which is the set of formulae that can be placed in Horn form by replacing some variables with their respective negation. Checking the existence of such a replacement can be done in linear time; therefore, the satisfiability of such formulae is in P as it can be solved by first performing this replacement and then checking the satisfiability of the resulting Horn formula.

[edit] Schaefer's dichotomy theorem

Main article: Schaefer's dichotomy theorem

The restrictions above (CNF, 2CNF, 3CNF, Horn) bound the considered formulae to be conjunction of subformulae; each restriction states a specific form for all subformulae: for example, only binary clauses can be subformulae in 2CNF.

Schaefer's dichotomy theorem states that, for any restriction to Boolean operators that can be used to form these subformulae, the corresponding satisfiability problem is in P or NP-complete. The membership in P of the satisfiability of 2CNF and Horn formulae are special cases of this theorem.

[edit] Runtime behavior

As mentioned briefly above, though the problem is NP-complete, many practical instances can be solved much more quickly. Many practical problems are actually "easy", so the SAT solver can easily find a solution, or prove that none exists, relatively quickly, even though the instance has thousands of variables and tens of thousands of constraints. Other much smaller problems exhibit run-times that are exponential in the problem size, and rapidly become impractical. Unfortunately, there is no reliable way to tell the difficulty of the problem without trying it. Therefore, almost all SAT solvers include time-outs, so they will terminate even if they cannot find a solution. Finally, different SAT solvers will find different instances easy or hard, and some excel at proving unsatisfiability, and others at finding solutions. All of these behaviors can be seen in the SAT solving contests.[1]

[edit] Extensions of SAT

An extension that has gained significant popularity since 2003 is Satisfiability modulo theories that can enrich CNF formulas with linear constraints, arrays, all-different constraints, uninterpreted functions, etc. Such extensions typically remain NP-complete, but very efficient solvers are now available that can handle many such kinds of constraints.

The satisfiability problem becomes more difficult (PSPACE-complete) if we allow quantifiers such as "for all" and "there exists" that bind the Boolean variables. An example of such an expression would be:

\forall x, \exists y,\exists z; (x \lor y \lor z) \land (\lnot x \lor \lnot y \lor \lnot z).

SAT itself uses only 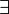\exists quantifiers. If we allow only 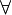\forall quantifiers, it becomes the Co-NP-complete tautology problem. If we allow both, the problem is called the quantified Boolean formula problem (QBF), which can be shown to be PSPACE-complete. It is widely believed that PSPACE-complete problems are strictly harder than any problem in NP, although this has not yet been proved.

A number of variants deal with the number of variable assignments making the formula true. Ordinary SAT asks if there is at least one such assignment. MAJSAT, which asks if the majority of all assignments make the formula true, is complete for PP, a probabilistic class. The problem of how many variable assignments satisfy a formula, not a decision problem, is in #P. UNIQUE-SAT or USAT is the problem of determining whether a formula known to have either zero or one satisfying assignments has zero or has one. Although this problem seems easier, it has been shown that if there is a practical (randomized polynomial-time) algorithm to solve this problem, then all problems in NP can be solved just as easily.

The maximum satisfiability problem, an FNP generalization of SAT, asks for the maximum number of clauses which can be satisfied by any assignment. It has efficient approximation algorithms, but is NP-hard to solve exactly. Worse still, it is APX-complete, meaning there is no polynomial-time approximation scheme (PTAS) for this problem unless P=NP.

[edit] Algorithms for solving SAT

There are two classes of high-performance algorithms for solving instances of SAT in practice: modern variants of the DPLL algorithm, such as Chaff, GRASP or march, and stochastic local search algorithms, such as WalkSAT.

A DPLL SAT solver employs a systematic backtracking search procedure to explore the (exponentially-sized) space of variable assignments looking for satisfying assignments. The basic search procedure was proposed in two seminal papers in the early 60s (see references below) and is now commonly referred to as the Davis-Putnam-Logemann-Loveland algorithm (“DPLL” or “DLL”).

Modern SAT solvers (developed in the last ten years) come in two flavors: "conflict-driven" and "look-ahead". Conflict-driven solvers augment the basic DPLL search algorithm with efficient conflict analysis, clause learning, non-chronological backtracking (aka backjumping), as well as "two-watched-literals" unit propagation, adaptive branching, and random restarts. These "extras" to the basic systematic search have been empirically shown to be essential for handling the large SAT instances that arise in Electronic Design Automation (EDA). Look-ahead solvers have especially strengthened reductions (going beyond unit-clause propagation) and the heuristics, and they are generally stronger than conflict-driven solvers on hard instances (while conflict-driven solvers can be much better on large instances which have inside actually an easy instance).

Modern SAT solvers are also having significant impact on the fields of software verification, constraint solving in artificial intelligence, and operations research, among others. Powerful solvers are readily available as free software, and are remarkably[citation needed] easy to use. In particular, the conflict-driven MiniSAT, which was relatively successful at the 2005 SAT competition, only has about 600 lines of code. An example for look-ahead solvers is march_dl, which won a prize at the 2007 SAT competition.

Genetic algorithms and other general-purpose stochastic local search methods are also being used to solve SAT problems, especially when there is no or limited knowledge of the specific structure of the problem instances to be solved. Certain types of large random satisfiable instances of SAT can be solved by survey propagation (SP). Particularly in hardware design and verification applications, satisfiability and other logical properties of a given propositional formula are sometimes decided based on a representation of the formula as a binary decision diagram (BDD).

Propositional satisfiability has various generalisations, including satisfiability for quantified Boolean formula problem, for first- and second-order logic, constraint satisfaction problems, 0-1 integer programming, and maximum satisfiability problem.

Many other decision problems, such as graph coloring problems, planning problems, and scheduling problems, can be easily encoded into SAT.

[edit] See also

[edit] References

  1. ^ "The international SAT Competitions web page". http://www.satcompetition.org/. Retrieved on 2007-11-15. 

[edit] External links

More information on SAT:

SAT Applications:

  • WinSAT: A Windows based SAT application made particularly for researchers.

SAT Solvers:

Conferences/Publications:

Benchmarks:

SAT solving in general:

This article includes material from a column in the ACM SIGDA e-newsletter by Prof. Karem Sakallah
 Original text is available here.

Retrieved from "http://en.wikipedia.org/wiki/Boolean_satisfiability_problem"
Personal tools