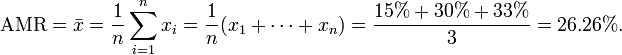cagr econ excel finance geometric growth productivity tip trick work

My tags:

From Wikipedia, the free encyclopedia

Compound Annual Growth Rate (CAGR) is a business and investing specific term for the geometric mean growth rate on an annualized basis.^[1] It represents the smoothed annualized gain earned over the investment time horizon. CAGR is not an accounting term, but remains widely used, particularly in growth industries or to compare the growth rates of two investments because CAGR dampens the effect of volatility of periodic returns that can render arithmetic means irrelevant. CAGR is often used to describe the growth over a period of time of some element of the business, for example revenue, units delivered, registered users, etc.

Contents 1 Formula 2 Example 3 References 4 See also

[edit] Formula

• V(t₀) : start value, V(t_n) : finish value, t_n − t₀ : number of years.
• Actual or normalized values may be used for calculation as long as they retain the same mathematical proportion^[2]
• The CAGR can also be calculated as the geometric mean of the decimal multiplier equivalents (i.e. +3% becomes 1.03 and -2% becomes 0.98) of the individual period-over-period changes.^[3]

[edit] Example

Say, the revenues of a company over four years, V(t) in above formula, have been:

Year	2004	2005	2006	2007
Revenues	100	115	150	200

t_n − t₀ = 2007 - 2004 = 3

Then, calculating CAGR gives:

For comparison:

• the Arithmetic Mean Return (AMR) would be the sum of annual returns divided by number of years or:

• the Arithmetic Return (AR) or simple return would be the ending value minus beginning value divided by the beginning value:

[edit] References

[edit] See also

• Geometric mean
• Arithmetic mean
• Rate_of_return#Average_annual_return_.28geometric.29