drudge3 famous heytesbury history historyofmath liberalarts mate math math-fieldtrip math115 mathematician mathematics mathqueue maths mth317n quizzlematerial termhomework thearg

My tags:

From Wikipedia, the free encyclopedia

The area of study known as the history of mathematics is primarily an investigation into the origin of discoveries in mathematics and, to a lesser extent, an investigation into the mathematical methods and notation of the past.

Before the modern age and the worldwide spread of knowledge, written examples of new mathematical developments have come to light only in a few locales. The most ancient mathematical texts available are Plimpton 322 (Babylonian mathematics c. 1900 BC), the Moscow Mathematical Papyrus (Egyptian mathematics c. 1850 BC), the Rhind Mathematical Papyrus (Egyptian mathematics c. 1650 BC), and the Shulba Sutras (Indian mathematics c. 800 BC). All of these texts concern the so-called Pythagorean theorem, which seems to be the most ancient and widespread mathematical development after basic arithmetic and geometry.

Egyptian and Babylonian mathematics were developed further in Greek and Hellenistic mathematics, which refined the methods (especially the introduction of mathematical rigor in proofs) and expanded the subject matter of mathematics.^[1] Islamic mathematics, in turn, developed and expanded the mathematics known to these ancient civilizations. Many Greek and Arabic texts on mathematics were then translated into Latin, which led to further development of mathematics in medieval Europe.

From ancient times through the Middle Ages, bursts of mathematical creativity were often followed by centuries of stagnation. Beginning in Renaissance Italy in the 16th century, new mathematical developments, interacting with new scientific discoveries, were made at an ever increasing pace, and this continues to the present day.

Contents 1 Early mathematics 2 Ancient Near East (c. 1800–500 BC) 2.1 Mesopotamia 2.2 Egypt 3 Ancient Indian mathematics (c. 900 BC–AD 200) 4 Greek and Hellenistic mathematics (c. 550 BC–AD 300) 5 Classical Chinese mathematics (c. 500 BC–AD 1300) 6 Classical Indian mathematics (c. 400–1600) 7 Islamic mathematics (c. 800–1500) 8 Medieval European mathematics (c. 500–1400) 8.1 Early Middle Ages (c. 500–1100) 8.2 Rebirth of mathematics in Europe (1100–1400) 9 Early modern European mathematics (c. 1400–1600) 10 17th century 11 18th century 12 19th century 13 20th century 14 See also 15 References 16 Further reading 17 External links

[edit] Early mathematics

Long before the earliest written records, there are drawings that indicate some knowledge of elementary mathematics and of time measurement based on the stars. For example, paleontologists have discovered ochre rocks in a South African cave that were about 70,000 years old, adorned with scratched geometric patterns.^[2] Also prehistoric artifacts discovered in Africa and France, dated between 35,000 and 20,000 years old,^[3] suggest early attempts to quantify time.^[4]

There is evidence that women devised counting to keep track of their menstrual cycles; 28 to 30 scratches on bone or stone, followed by a distinctive marker. Moreover, hunters and herders employed the concepts of one, two, and many, as well as the idea of none or zero, when considering herds of animals.^[5][6]

The Ishango bone, found near the headwaters of the Nile river (northeastern Congo), may be as much as 20,000 years old. One common interpretation is that the bone is the earliest known demonstration^[7] of sequences of prime numbers and of Ancient Egyptian multiplication. Predynastic Egyptians of the 5th millennium BC pictorially represented geometric spatial designs. It has been claimed that megalithic monuments in England and Scotland, dating from the 3rd millennium BC, incorporate geometric ideas such as circles, ellipses, and Pythagorean triples in their design.^[8]

The earliest known mathematics in ancient India dates from 3000–2600 BC in the Indus Valley Civilization (Harappan civilization) of North India and Pakistan. This civilization developed a system of uniform weights and measures that used the decimal system, a surprisingly advanced brick technology which utilized ratios, streets laid out in perfect right angles, and a number of geometrical shapes and designs, including cuboids, barrels, cones, cylinders, and drawings of concentric and intersecting circles and triangles. Mathematical instruments included an accurate decimal ruler with small and precise subdivisions, a shell instrument that served as a compass to measure angles on plane surfaces or in horizon in multiples of 40–360 degrees, a shell instrument used to measure 8–12 whole sections of the horizon and sky, and an instrument for measuring the positions of stars for navigational purposes. The Indus script has not yet been deciphered; hence very little is known about the written forms of Harappan mathematics. Archeological evidence has led some to suspect that this civilization used a base 8 numeral system and had a value of π, the ratio of the length of the circumference of the circle to its diameter.^[9]

The earliest extant Chinese mathematics dates from the Shang Dynasty (1600–1046 BC), and consists of numbers scratched on a tortoise shell [1] [2]. These numbers were represented by means of a decimal notation. For example, the number 123 is written (from top to bottom) as the symbol for 1 followed by the symbol for 100, then the symbol for 2 followed by the symbol for 10, then the symbol for 3. This was the most advanced number system in the world at the time, and allowed calculations to be carried out on the suan pan or (Chinese abacus). The date of the invention of the suan pan is not certain, but the earliest written mention dates from AD 190, in Xu Yue's Supplementary Notes on the Art of Figures.

[edit] Ancient Near East (c. 1800–500 BC)

[edit] Mesopotamia

Babylonian mathematics refers to any mathematics of the people of Mesopotamia (modern Iraq) from the days of the early Sumerians until the beginning of the Hellenistic period. It is named Babylonian mathematics due to the central role of Babylon as a place of study, which ceased to exist during the Hellenistic period. From this point, Babylonian mathematics merged with Greek and Egyptian mathematics to give rise to Hellenistic mathematics. Later under the Arab Empire, Mesopotamia, especially Baghdad, once again became an important center of study for Islamic mathematics.

In contrast to the sparsity of sources in Egyptian mathematics, our knowledge of Babylonian mathematics is derived from more than 400 clay tablets unearthed since the 1850s. Written in Cuneiform script, tablets were inscribed whilst the clay was moist, and baked hard in an oven or by the heat of the sun. Some of these appear to be graded homework.

The earliest evidence of written mathematics dates back to the ancient Sumerians, who built the earliest civilization in Mesopotamia. They developed a complex system of metrology from 3000 BC. From around 2500 BC onwards, the Sumerians wrote multiplication tables on clay tablets and dealt with geometrical exercises and division problems. The earliest traces of the Babylonian numerals also date back to this period.^[10]

The majority of recovered clay tablets date from 1800 to 1600 BC, and cover topics which include fractions, algebra, quadratic and cubic equations, and the calculation of regular reciprocal pairs (see Plimpton 322).^[11] The tablets also include multiplication tables and methods for solving linear and quadratic equations. The Babylonian tablet YBC 7289 gives an approximation to √2 accurate to five decimal places.

Babylonian mathematics were written using a sexagesimal (base-60) numeral system. From this we derive the modern day usage of 60 seconds in a minute, 60 minutes in an hour, and 360 (60 x 6) degrees in a circle, as well as the use of seconds and minutes of arc to denote fractions of a degree. Babylonian advances in mathematics were facilitated by the fact that 60 has many divisors. Also, unlike the Egyptians, Greeks, and Romans, the Babylonians had a true place-value system, where digits written in the left column represented larger values, much as in the decimal system. They lacked, however, an equivalent of the decimal point, and so the place value of a symbol often had to be inferred from the context.

[edit] Egypt

Egyptian mathematics refers to mathematics written in the Egyptian language. From the Hellenistic period, Greek replaced Egyptian as the written language of Egyptian scholars, and from this point Egyptian mathematics merged with Greek and Babylonian mathematics to give rise to Hellenistic mathematics. Mathematical study in Egypt later continued under the Arab Empire as part of Islamic mathematics, when Arabic became the written language of Egyptian scholars.

The oldest mathematical text discovered so far is the Moscow papyrus, which is an Egyptian Middle Kingdom papyrus dated c. 2000–1800 BC.^{[citations needed]} Like many ancient mathematical texts, it consists of what are today called word problems or story problems, which were apparently intended as entertainment. One problem is considered to be of particular importance because it gives a method for finding the volume of a frustum: "If you are told: A truncated pyramid of 6 for the vertical height by 4 on the base by 2 on the top. You are to square this 4, result 16. You are to double 4, result 8. You are to square 2, result 4. You are to add the 16, the 8, and the 4, result 28. You are to take one third of 6, result 2. You are to take 28 twice, result 56. See, it is 56. You will find it right."

The Rhind papyrus (c. 1650 BC [3]) is another major Egyptian mathematical text, an instruction manual in arithmetic and geometry. In addition to giving area formulas and methods for multiplication, division and working with unit fractions, it also contains evidence of other mathematical knowledge^[12], including composite and prime numbers; arithmetic, geometric and harmonic means; and simplistic understandings of both the Sieve of Eratosthenes and perfect number theory (namely, that of the number 6)[4]. It also shows how to solve first order linear equations [5] as well as arithmetic and geometric series [6].

Also, three geometric elements contained in the Rhind papyrus suggest the simplest of underpinnings to analytical geometry: (1) first and foremost, how to obtain an approximation of π accurate to within less than one percent; (2) second, an ancient attempt at squaring the circle; and (3) third, the earliest known use of a kind of cotangent.

Finally, the Berlin papyrus (c. 1300 BC [7] [8]) shows that ancient Egyptians could solve a second-order algebraic equation [9].

[edit] Ancient Indian mathematics (c. 900 BC–AD 200)

Vedic mathematics began in the early Iron Age, with the Shatapatha Brahmana (c. 9th century BC), which approximates the value of π to 2 decimal places.^[10], and the Sulba Sutras (c. 800–500 BC) were geometry texts that used irrational numbers, prime numbers, the rule of three and cube roots; computed the square root of 2 to five decimal places; gave the method for squaring the circle; solved linear equations and quadratic equations; developed Pythagorean triples algebraically and gave a statement and numerical proof of the Pythagorean theorem.

Pāṇini (c. 5th century BC) formulated the grammar rules for Sanskrit. His notation was similar to modern mathematical notation, and used metarules, transformations, and recursions with such sophistication that his grammar had the computing power equivalent to a Turing machine. Pingala (roughly 3rd-1st centuries BC) in his treatise of prosody uses a device corresponding to a binary numeral system. His discussion of the combinatorics of meters, corresponds to the binomial theorem. Pingala's work also contains the basic ideas of Fibonacci numbers (called mātrāmeru). The Brāhmī script was developed at least from the Maurya dynasty in the 4th century BC, with recent archeological evidence appearing to push back that date to around 600 BC. The Brahmi numerals date to the 3rd century BC.

Between 400 BC and AD 200, Jaina mathematicians began studying mathematics for the sole purpose of mathematics. They were the first to develop transfinite numbers, set theory, logarithms, fundamental laws of indices, cubic equations, quartic equations, sequences and progressions, permutations and combinations, squaring and extracting square roots, and finite and infinite powers. The Bakhshali Manuscript written between 200 BC and AD 200 included solutions of linear equations with up to five unknowns, the solution of the quadratic equation, arithmetic and geometric progressions, compound series, quadratic indeterminate equations, simultaneous equations, and the use of zero and negative numbers. Accurate computations for irrational numbers could be found, which includes computing square roots of numbers as large as a million to at least 11 decimal places.

[edit] Greek and Hellenistic mathematics (c. 550 BC–AD 300)

Greek mathematics refers to mathematics written in the Greek language between about 600 BC and AD 300.^[13] Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to North Africa, but were united by culture and language. Greek mathematics of the period following Alexander the Great is sometimes called Hellenistic mathematics.

Greek mathematics was more sophisticated than the mathematics that had been developed by earlier cultures. All surviving records of pre-Greek mathematics show the use of inductive reasoning, that is, repeated observations used to establish rules of thumb. Greek mathematicians, by contrast, used deductive reasoning. The Greeks used logic to derive conclusions from definitions and axioms.^[14]

Greek mathematics is thought to have begun with Thales (c. 624–c.546 BC) and Pythagoras (c. 582–c. 507 BC). Although the extent of the influence is disputed, they were probably inspired by the mathematics of Egypt, Mesopotamia and India. According to legend, Pythagoras traveled to Egypt to learn mathematics, geometry, and astronomy from Egyptian priests.

Thales used geometry to solve problems such as calculating the height of pyramids and the distance of ships from the shore. Pythagoras is credited with the first proof of the Pythagorean theorem, though the statement of the theorem has a long history.^[15] In his commentary on Euclid, Proclus states that Pythagoras expressed the theorem that bears his name and constructed Pythagorean triples algebraically rather than geometrically. The Academy of Plato had the motto, "Let none unversed in geometry enter here".

The Pythagoreans proved the existence of irrational numbers. Eudoxus (408–c.355 BC) developed the method of exhaustion, a precursor of modern integration. Aristotle (384—c.322 BC) first wrote down the laws of logic. Euclid (c. 300 BC) is the earliest example of the format still used in mathematics today, definition, axiom, theorem, proof. He also studied conics. His book, Elements, was known to all educated people in the West until the middle of the 20th century.^[16] In addition to the familiar theorems of geometry, such as the Pythagorean theorem, Elements includes a proof that the square root of two is irrational and that there are infinitely many prime numbers. The Sieve of Eratosthenes (c. 230 BC) was used to discover prime numbers.

Archimedes (c.287–212 BC) of Syracuse used the method of exhaustion to calculate the area under the arc of a parabola with the summation of an infinite series, and gave remarkably accurate approximations of Pi.^[17] He also studied the spiral bearing his name, formulas for the volumes of surfaces of revolution, and an ingenious system for expressing very large numbers.

[edit] Classical Chinese mathematics (c. 500 BC–AD 1300)

In China, the Emperor Qin Shi Huang (Shi Huang-ti) commanded in 212 BC that all books outside of Qin state to be burned. It was not universally obeyed, but as a consequence of this order little is known about ancient Chinese mathematics.

From the Western Zhou Dynasty (from 1046 BC), the oldest mathematical work to survive the book burning is the I Ching, which uses the 8 binary 3-tuples (trigrams) and 64 binary 6-tuples (hexagrams) for philosophical, mathematical, and mystical purposes. The binary tuples are composed of broken and solid lines, called yin (female) and yang (male), respectively (see King Wen sequence).

The oldest existent work on geometry in China comes from the philosophical Mohist canon c. 330 BC, compiled by the followers of Mozi (470–390 BC). The Mo Jing described various aspects of many fields associated with physical science, and provided a small wealth of information on mathematics as well.

After the book burning, the Han dynasty (202 BC–220 AD) produced works of mathematics which presumably expand on works that are now lost. The most important of these is The Nine Chapters on the Mathematical Art, the full title of which appeared by AD 179, but existed in part under other titles beforehand. It consists of 246 word problems involving agriculture, business, employment of geometry to figure height spans and dimension ratios for Chinese pagoda towers, engineering, surveying, and includes material on right triangles and π. It also made use of Cavalieri's principle on volume more than a thousand years before Cavalieri would propose it in the West. It created mathematical proof for the Pythagorean theorem, and a mathematical formula for Gaussian elimination. Liu Hui commented on the work by the 3rd century AD.

In addition, the mathematical works of the Han astronomer and inventor Zhang Heng (AD 78–139) had a formulation for pi as well, which differed from Liu Hui's calculation. Zhang Heng used his formula of pi to find spherical volume. There was also the written work of the mathematician and music theorist Jing Fang (78–37 BC); by using the Pythagorean comma, Jing observed that 53 just fifths approximates 31 octaves. This would later lead to the discovery of 53 equal temperament, and was not calculated precisely elsewhere until the German Nicholas Mercator did so in the 17th century.

The Chinese also made use of the complex combinatorial diagram known as the magic square and magic circles, described in ancient times and perfected by Yang Hui (AD 1238–1398).

Zu Chongzhi (5th century) of the Southern and Northern Dynasties computed the value of π to seven decimal places, which remained the most accurate value of π for almost 1000 years.

Even after European mathematics began to flourish during the Renaissance, European and Chinese mathematics were separate traditions, with significant Chinese mathematical output in decline, until the Jesuit missionaries such as Matteo Ricci carried mathematical ideas back and forth between the two cultures from the 16th to 18th centuries.

[edit] Classical Indian mathematics (c. 400–1600)

The Surya Siddhanta (c. 400) introduced the trigonometric functions of sine, cosine, and inverse sine, and laid down rules to determine the true motions of the luminaries, which conforms to their actual positions in the sky. The cosmological time cycles explained in the text, which was copied from an earlier work, corresponds to an average sidereal year of 365.2563627 days, which is only 1.4 seconds longer than the modern value of 365.25636305 days. This work was translated into to Arabic and Latin during the Middle Ages.

Aryabhata, in 499, introduced the versine function, produced the first trigonometric tables of sine, developed techniques and algorithms of algebra, infinitesimals, differential equations, and obtained whole number solutions to linear equations by a method equivalent to the modern method, along with accurate astronomical calculations based on a heliocentric system of gravitation. An Arabic translation of his Aryabhatiya was available from the 8th century, followed by a Latin translation in the 13th century. He also computed the value of π to the fourth decimal place as 3.1416. In the 14th century, Madhava of Sangamagrama computed the value of π to the eleventh decimal place as 3.14159265359.

In the 7th century, Brahmagupta identified the Brahmagupta theorem, Brahmagupta's identity and Brahmagupta's formula, and for the first time, in Brahma-sphuta-siddhanta, he lucidly explained the use of zero as both a placeholder and decimal digit, and explained the Hindu-Arabic numeral system. It was from a translation of this Indian text on mathematics (c. 770) that Islamic mathematicians were introduced to this numeral system, which they adapted as Arabic numerals. Islamic scholars carried knowledge of this number system to Europe by the 12th century, and it has now displaced all older number systems throughout the world. In the 10th century, Halayudha's commentary on Pingala's work contains a study of the Fibonacci sequence and Pascal's triangle, and describes the formation of a matrix.

In the 12th century, Bhaskara first conceived differential calculus, along with the concepts of the derivative, differential coefficient and differentiation. He also stated Rolle's theorem (a special case of the mean value theorem), studied Pell's equation, and investigated the derivative of the sine function. From the 14th century, Madhava and other Kerala School mathematicians further developed his ideas. They developed the concepts of mathematical analysis and floating point numbers, and concepts fundamental to the overall development of calculus, including the mean value theorem, term by term integration, the relationship of an area under a curve and its antiderivative or integral, the integral test for convergence, iterative methods for solutions to non-linear equations, and a number of infinite series, power series, Taylor series, and trigonometric series. In the 16th century, Jyeshtadeva consolidated many of the Kerala School's developments and theorems in the Yuktibhasa, the world's first differential calculus text, which also introduced concepts of integral calculus.

Mathematical progress in India stagnated from the late 16th century onwards due to political turmoil.

[edit] Islamic mathematics (c. 800–1500)

The Islamic Arab Empire established across the Middle East, Central Asia, North Africa, Iberia, and in parts of India in the 8th century made significant contributions towards mathematics. Although most Islamic texts on mathematics were written in Arabic, they were not all written by Arabs, since much like the status of Greek in the Hellenistic world, Arabic was used as the written language of non-Arab scholars throughout the Islamic world at the time. Alongside Arabs, many important Islamic mathematicians were also Persians.

In the 9th century, Muḥammad ibn Mūsā al-Ḵwārizmī wrote several important books on the Hindu-Arabic numerals and on methods for solving equations. His book On the Calculation with Hindu Numerals, written about 825, along with the work of Al-Kindi, were instrumental in spreading Indian mathematics and Indian numerals to the West. The word algorithm is derived from the Latinization of his name, Algoritmi, and the word algebra from the title of one of his works, Al-Kitāb al-mukhtaṣar fī hīsāb al-ğabr wa’l-muqābala (The Compendious Book on Calculation by Completion and Balancing). Al-Khwarizmi is often called the "father of algebra", for his fundamental contributions to the field.^[18] He gave an exhaustive explanation for the algebraic solution of quadratic equations with positive roots,^[19] and he was the first to teach algebra in an elementary form and for its own sake.^[20] He also introduced the fundamental method of "reduction" and "balancing", referring to the transposition of subtracted terms to the other side of an equation, that is, the cancellation of like terms on opposite sides of the equation. This is the operation which Al-Khwarizmi originally described as al-jabr.^[21] His algebra was also no longer concerned "with a series of problems to be resolved, but an exposition which starts with primitive terms in which the combinations must give all possible prototypes for equations, which henceforward explicitly constitute the true object of study." He also studied an equation for its own sake and "in a generic manner, insofar as it does not simply emerge in the course of solving a problem, but is specifically called on to define an infinite class of problems."^[22]

Further developments in algebra were made by Al-Karaji in his treatise al-Fakhri, where he extends the methodology to incorporate integer powers and integer roots of unknown quantities. The first known proof by mathematical induction appears in a book written by Al-Karaji around 1000 AD, who used it to prove the binomial theorem, Pascal's triangle, and the sum of integral cubes.^[23] The historian of mathematics, F. Woepcke,^[24] praised Al-Karaji for being "the first who introduced the theory of algebraic calculus." Also in the 10th century, Abul Wafa translated the works of Diophantus into Arabic and developed the tangent function. Ibn al-Haytham was the first mathematician to derive the formula for the sum of the fourth powers, using a method that is readily generalizable for determining the general formula for the sum of any integral powers. He performed an integration in order to find the volume of a paraboloid, and was able to generalize his result for the integrals of polynomials up to the fourth degree. He thus came close to finding a general formula for the integrals of polynomials, but he was not concerned with any polynomials higher than the fourth degree.^[25]

In the late 11th century, Omar Khayyam wrote Discussions of the Difficulties in Euclid, a book about flaws in Euclid's Elements, especially the parallel postulate, and laid the foundations for analytic geometry and non-Euclidean geometry.^{[citation needed]} He was also the first to find the general geometric solution to cubic equations. He was also very influential in calendar reform.^{[citation needed]}

In the late 12th century, Sharaf al-Dīn al-Tūsī introduced the concept of a function,^[26] and he was the first to discover the derivative of cubic polynomials.^[27] His Treatise on Equations developed concepts related to differential calculus, such as the derivative function and the maxima and minima of curves, in order to solve cubic equations which may not have positive solutions.^[28]

In the 13th century, Nasir al-Din Tusi (Nasireddin) made advances in spherical trigonometry. He also wrote influential work on Euclid's parallel postulate. In the 15th century, Ghiyath al-Kashi computed the value of π to the 16th decimal place. Kashi also had an algorithm for calculating nth roots, which was a special case of the methods given many centuries later by Ruffini and Horner.

Other notable Muslim mathematicians included al-Samawal, Abu'l-Hasan al-Uqlidisi, Jamshid al-Kashi, Thabit ibn Qurra, Abu Kamil and Abu Sahl al-Kuhi.

Other achievements of Muslim mathematicians during this period include the development of algebra and algorithms (see Muhammad ibn Mūsā al-Khwārizmī), the development of spherical trigonometry,^[29] the addition of the decimal point notation to the Arabic numerals, the discovery of all the modern trigonometric functions besides the sine, al-Kindi's introduction of cryptanalysis and frequency analysis, the development of analytic geometry by Ibn al-Haytham, the beginning of algebraic geometry by Omar Khayyam, the first refutations of Euclidean geometry and the parallel postulate by Nasīr al-Dīn al-Tūsī, the first attempt at a non-Euclidean geometry by Sadr al-Din, the development of an algebraic notation by al-Qalasādī,^[30] and many other advances in algebra, arithmetic, calculus, cryptography, geometry, number theory and trigonometry.

During the time of the Ottoman Empire from the 15th century, the development of Islamic mathematics became stagnant.

[edit] Medieval European mathematics (c. 500–1400)

Medieval European interest in mathematics was driven by concerns quite different from those of modern mathematicians. One driving element was the belief that mathematics provided the key to understanding the created order of nature, frequently justified by Plato's Timaeus and the biblical passage that God had "ordered all things in measure, and number, and weight" (Wisdom 11:21).

[edit] Early Middle Ages (c. 500–1100)

Boethius provided a place for mathematics in the curriculum when he coined the term quadrivium to describe the study of arithmetic, geometry, astronomy, and music. He wrote De institutione arithmetica, a free translation from the Greek of Nicomachus's Introduction to Arithmetic; De institutione musica, also derived from Greek sources; and a series of excerpts from Euclid's Elements. His works were theoretical, rather than practical, and were the basis of mathematical study until the recovery of Greek and Arabic mathematical works.^[31][32]

[edit] Rebirth of mathematics in Europe (1100–1400)

In the 12th century, European scholars traveled to Spain and Sicily seeking scientific Arabic texts, including al-Khwarizmi's The Compendious Book on Calculation by Completion and Balancing, translated into Latin by Robert of Chester, and the complete text of Euclid's Elements, translated in various versions by Adelard of Bath, Herman of Carinthia, and Gerard of Cremona.^[33][34]

These new sources sparked a renewal of mathematics. Fibonacci, writing in the Liber Abaci, in 1202 and updated in 1254, produced the first significant mathematics in Europe since the time of Eratosthenes, a gap of more than a thousand years. The work introduced Hindu-Arabic numerals to Europe, and discussed many other mathematical problems.

The fourteenth century saw the development of new mathematical concepts to investigate a wide range of problems.^[35] One important contribution was development of mathematics of local motion.

Thomas Bradwardine proposed that speed (V) increases in arithmetic proportion as the ratio of force (F) to resistance (R) increases in geometric proportion. Bradwardine expressed this by a series of specific examples, but although the logarithm had not yet been conceived, we can express his conclusion anachronistically by writing: V = log (F/R).^[36] Bradwardine's analysis is an example of transferring a mathematical technique used by al-Kindi and Arnald of Villanova to quantify the nature of compound medicines to a different physical problem.^[37]

One of the 14th-century Oxford Calculators, William Heytesbury, lacking differential calculus and the concept of limits, proposed to measure instantaneous speed "by the path that would be described by [a body] if ... it were moved uniformly at the same degree of speed with which it is moved in that given instant".^[38]

Heytesbury and others mathematically determined the distance covered by a body undergoing uniformly accelerated motion (today solved by integration), stating that "a moving body uniformly acquiring or losing that increment [of speed] will traverse in some given time a [distance] completely equal to that which it would traverse if it were moving continuously through the same time with the mean degree [of speed]".^[39]

Nicole Oresme at the University of Paris and the Italian Giovanni di Casali independently provided graphical demonstrations of this relationship, asserting that the area under the line depicting the constant acceleration, represented the total distance traveled.^[40] In a later mathematical commentary on Euclid's Elements, Oresme made a more detailed general analysis in which he demonstrated that a body will acquire in each successive increment of time an increment of any quality that increases as the odd numbers. Since Euclid had demonstrated the sum of the odd numbers are the square numbers, the total quality acquired by the body increases as the square of the time.^[41]

[edit] Early modern European mathematics (c. 1400–1600)

In Europe at the dawn of the Renaissance, mathematics was still limited by the cumbersome notation using Roman numerals and expressing relationships using words, rather than symbols: there was no plus sign, no equal sign, and no use of x as an unknown.^{[citation needed]}

In 16th century European mathematicians began to make advances without precedent anywhere in the world, so far as is known today. The first of these was the general solution of cubic equations, generally credited to Scipione del Ferro c. 1510, but first published by Johannes Petreius in Nuremberg in Gerolamo Cardano's Ars magna, which also included the solution of the general quartic equation from Cardano's student Lodovico Ferrari .

From this point on, mathematical developments came swiftly, contributing to and benefiting from contemporary advances in the physical sciences. This progress was greatly aided by advances in printing. The earliest mathematical books printed were Peurbach's Theoricae nova planetarum (1472}, followed by a book on commercial arithmetic, the Treviso Arithmetic (1478), and then the first extant book on mathematics, Euclid's Elements, printed and published by Ratdolt in 1482.

Driven by the demands of navigation and the growing need for accurate maps of large areas, trigonometry grew to be a major branch of mathematics. Bartholomaeus Pitiscus was the first to use the word, publishing his Trigonometria in 1595. Regiomontanus's table of sines and cosines was published in 1533.^[42]

By century's end, thanks to Regiomontanus (1436–76) and François Vieta (1540–1603), among others, mathematics was written using Hindu-Arabic numerals and in a form not too different from the notation used today.

[edit] 17th century

The 17th century saw an unprecedented explosion of mathematical and scientific ideas across Europe. Galileo, an Italian, observed the moons of Jupiter in orbit about that planet, using a telescope based on a toy imported from Holland. Tycho Brahe, a Dane, had gathered an enormous quantity of mathematical data describing the positions of the planets in the sky. His student, Johannes Kepler, a German, began to work with this data. In part because he wanted to help Kepler in his calculations, John Napier, in Scotland, was the first to investigate natural logarithms. Kepler succeeded in formulating mathematical laws of planetary motion. The analytic geometry developed by René Descartes (1596–1650), a French mathematician and philosopher, allowed those orbits to be plotted on a graph, in Cartesian coordinates.

Building on earlier work by many prececessors, Isaac Newton, an Englishman, discovered the laws of physics explaining Kepler's Laws, and brought together the concepts now known as calculus. Independently, Gottfried Wilhelm Leibniz, in Germany, developed calculus and much of the calculus notation still in use today. Science and mathematics had become an international endeavor, which would soon spread over the entire world.^[43]

In addition to the application of mathematics to the studies of the heavens, applied mathematics began to expand into new areas, with the correspondence of Pierre de Fermat and Blaise Pascal. Pascal and Fermat set the groundwork for the investigations of probability theory and the corresponding rules of combinatorics in their discussions over a game of gambling. Pascal, with his wager, attempted to use the newly developing probability theory to argue for a life devoted to religion, on the grounds that even if the probability of success was small, the rewards were infinite. In some sense, this foreshadowed the development of utility theory in the 18th–19th century.

[edit] 18th century

The most influential mathematician of the 1700s was arguably Leonhard Euler. His contributions range from founding the study of graph theory with the Seven Bridges of Königsberg problem to standardizing many modern mathematical terms and notations. For example, he named the square root of minus 1 with the symbol i, and he popularized the use of the Greek letter π to stand for the ratio of a circle's circumference to its diameter. He made numerous contributions to the study of topology, graph theory, calculus, combinatorics, and complex analysis, as evidenced by the multitude of theorems and notations named for him.

Other important European mathematicians of the 18th century included Joseph Louis Lagrange, who did pioneering work in number theory, algebra, differential calculus, and the calculus of variations, and Laplace who, in the age of Napoleon did important work on the foundations of celestial mechanics and on statistics.

[edit] 19th century

Throughout the 19th century mathematics became increasingly abstract. In the 19th century lived Carl Friedrich Gauss (1777–1855). Leaving aside his many contributions to science, in pure mathematics he did revolutionary work on functions of complex variables, in geometry, and on the convergence of series. He gave the first satisfactory proofs of the fundamental theorem of algebra and of the quadratic reciprocity law.

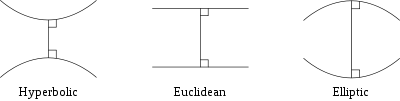
This century saw the development of the two forms of non-Euclidean geometry, where the parallel postulate of Euclidean geometry no longer holds. The Russian mathematician Nikolai Ivanovich Lobachevsky and his rival, the Hungarian mathematician Janos Bolyai, independently defined and studied hyperbolic geometry, where uniqueness of parallels no longer holds. In this geometry the sum of angles in a triangle add up to less than 180°. Elliptic geometry was developed later in the 19th century by the German mathematician Bernhard Riemann; here no parallel can be found and the angles in a triangle add up to more than 180°. Riemann also developed Riemannian geometry, which unifies and vastly generalizes the three types of geometry, and he defined the concept of a manifold, which generalize the ideas of curves and surfaces.

The 19th century saw the beginning of a great deal of abstract algebra. William Rowan Hamilton in Ireland developed noncommutative algebra. The British mathematician George Boole devised an algebra that soon evolved into what is now called Boolean algebra, in which the only numbers were 0 and 1 and in which, famously, 1 + 1 = 1. Boolean algebra is the starting point of mathematical logic and has important applications in computer science.

Augustin-Louis Cauchy, Bernhard Riemann, and Karl Weierstrass reformulated the calculus in a more rigorous fashion.

Also, for the first time, the limits of mathematics were explored. Niels Henrik Abel, a Norwegian, and Évariste Galois, a Frenchman, proved that there is no general algebraic method for solving polynomial equations of degree greater than four. Other 19th century mathematicians utilized this in their proofs that straightedge and compass alone are not sufficient to trisect an arbitrary angle, to construct the side of a cube twice the volume of a given cube, nor to construct a square equal in area to a given circle. Mathematicians had vainly attempted to solve all of these problems since the time of the ancient Greeks.

Abel and Galois's investigations into the solutions of various polynomial equations laid the groundwork for further developments of group theory, and the associated fields of abstract algebra. In the 20th century physicists and other scientists have seen group theory as the ideal way to study symmetry.

In the later 19th century, Georg Cantor established the first foundations of set theory, which enabled the rigorous treatment of the notion of infinity and has become the common language of nearly all mathematics. Cantor's set theory, and the rise of mathematical logic in the hands of Peano, L. E. J. Brouwer, David Hilbert, Bertrand Russell, and A.N. Whitehead, initiated a long running debate on the foundations of mathematics.

The 19th century saw the founding of a number of national mathematical societies: the London Mathematical Society in 1865, the Société Mathématique de France in 1872, the Circolo Mathematico di Palermo in 1884, the Edinburgh Mathematical Society in 1883, and the American Mathematical Society in 1888.

[edit] 20th century

The 20th century saw mathematics become a major profession. Every year, thousands of new Ph.D.s in mathematics are awarded, and jobs are available in both teaching and industry. In earlier centuries, there were few creative mathematicians in the world at any one time. For the most part, mathematicians were either born to wealth, like Napier, or supported by wealthy patrons, like Gauss. A few, like Fourier, derived meager livelihoods from teaching in universities. Niels Henrik Abel, unable to obtain a position, died in poverty of malnutrition and tuberculosis at the age of twenty-six.

In a 1900 speech to the International Congress of Mathematicians, David Hilbert set out a list of 23 unsolved problems in mathematics. These problems, spanning many areas of mathematics, formed a central focus for much of 20th century mathematics. Today, 10 have been solved, 7 are partially solved, and 2 are still open. The remaining 4 are too loosely formulated to be stated as solved or not.

Famous historical conjectures were finally proved. In 1976, Wolfgang Haken and Kenneth Appel used a computer to prove the four color theorem. Andrew Wiles, building on the work of others, proved Fermat's Last Theorem in 1995. Paul Cohen and Kurt Gödel proved that the continuum hypothesis is independent of (could neither be proved nor disproved from) the standard axioms of set theory.

Mathematical collaborations of unprecedented size and scope took place. A famous example is the classification of finite simple groups (also called the "enormous theorem"), whose proof between 1955 and 1983 required 500-odd journal articles by about 100 authors, and filling tens of thousands of pages. A group of French mathematicians, including Jean Dieudonné and André Weil, publishing under the pseudonym "Nicolas Bourbaki," attempted to exposit all of known mathematics as a coherent rigorous whole. The resulting several dozen volumes has had a controversial influence on mathematical education.^[44]

Entire new areas of mathematics such as mathematical logic, topology, complexity theory, and game theory changed the kinds of questions that could be answered by mathematical methods.

At the same time, deep insights were made about the limitations to mathematics. In 1929 and 1930, it was proved the truth or falsity of all statements formulated about the natural numbers plus one of addition and multiplication, was decidable, i.e., could be determined by algorithm. In 1931, Kurt Gödel found that this was not the case for the natural numbers plus both addition and multiplication; this system, known as Peano arithmetic, was in fact incompletable. (Peano arithmetic is adequate for a good deal of number theory, including the notion of prime number.) A consequence of Gödel's two incompleteness theorems is that in any mathematical system that includes Peano arithmetic (including all of analysis and geometry), truth necessarily outruns proof; there are true statements that cannot be proved within the system. Hence mathematics cannot be reduced to mathematical logic, and David Hilbert's dream of making all of mathematics complete and consistent died.

One of the more colorful figures in 20th century mathematics was Srinivasa Aiyangar Ramanujan (1887–1920) who, despite being largely self-educated, conjectured or proved over 3000 theorems, including properties of highly composite numbers, the partition function and its asymptotics, and mock theta functions. He also made major investigations in the areas of gamma functions, modular forms, divergent series, hypergeometric series and prime number theory.

[edit] See also

• List of important publications in mathematics
• History of algebra
• History of calculus
• History of combinatorics
• History of geometry
• History of logic
• History of mathematical notation
• History of statistics
• History of trigonometry
• History of writing numbers

[edit] References

[edit] Further reading

[edit] External links

• MacTutor History of Mathematics archive (John J. O'Connor and Edmund F. Robertson; University of St Andrews, Scotland). An award-winning website containing detailed biographies on many historical and contemporary mathematicians, as well as information on famous curves and various topics in the history of mathematics.
• History of Mathematics Home Page (David E. Joyce; Clark University). Articles on various topics in the history of mathematics with an extensive bibliography.
• The History of Mathematics (David R. Wilkins; Trinity College, Dublin). Collections of material on the mathematics between the 17th and 19th century.
• History of Mathematics (Simon Fraser University).
• Earliest Known Uses of Some of the Words of Mathematics (Jeff Miller). Contains information on the earliest known uses of terms used in mathematics.
• Earliest Uses of Various Mathematical Symbols (Jeff Miller). Contains information on the history of mathematical notations.
• Biographies of Women Mathematicians (Larry Riddle; Agnes Scott College).
• Mathematicians of the African Diaspora (Scott W. Williams; University at Buffalo).
• Fred Rickey's History of Mathematics Page
• A Bibliography of Collected Works and Correspondence of Mathematicians (Steven W. Rockey; Cornell University Library).
• Mathourism - Places with a mathematical historic interest

Journals

• Convergence, the Mathematical Association of America's online Math History Magazine

Directories

• Links to Web Sites on the History of Mathematics (The British Society for the History of Mathematics)
• History of Mathematics Math Archives (University of Tennessee, Knoxville)
• History/Biography The Math Forum (Drexel University)
• History of Mathematics (Courtright Memorial Library).
• History of Mathematics Web Sites (David Calvis; Baldwin-Wallace College)
• History of mathematics at the Open Directory Project
• Historia de las Matemáticas (Universidad de La La guna)
• História da Matemática (Universidade de Coimbra)
• Using History in Math Class
• Mathematical Resources: History of Mathematics (Bruno Kevius)
• History of Mathematics (Roberta Tucci)