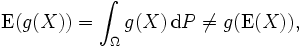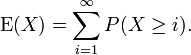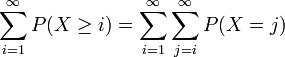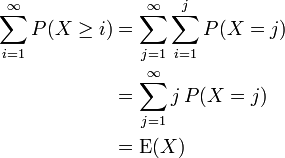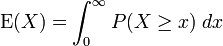Expected value
From Wikipedia, the free encyclopedia
In probability theory and statistics, the expected value (or expectation value, or mathematical expectation, or mean, or first moment) of a random variable is the integral of the random variable with respect to its probability measure. For discrete random variables this is equivalent to the probability-weighted sum of the possible values, and for continuous random variables with a density function it is the probability density -weighted integral of the possible values.
The term "expected value" can be misleading. It must not be confused with the "most probable value." The expected value is in general not a typical value that the random variable can take on. It is often helpful to interpret the expected value of a random variable as the long-run average value of the variable over many independent repetitions of an experiment.
The expected value may be intuitively understood by the law of large numbers: The expected value, when it exists, is almost surely the limit of the sample mean as sample size grows to infinity. The value may not be expected in the general sense – the "expected value" itself may be unlikely or even impossible (such as having 2.5 children), just like the sample mean. The expected value does not exist for all distributions, such as the Cauchy distribution.
It is possible to construct an expected value equal to the probability of an event by taking the expectation of an indicator function that is one if the event has occurred and zero otherwise. This relationship can be used to translate properties of expected values into properties of probabilities, e.g. using the law of large numbers to justify estimating probabilities by frequencies.
Contents |
[edit] Examples
The expected value from the roll of an ordinary six-sided die is
which is not among the possible outcomes.
A common application of expected value is gambling. For example, an American roulette wheel has 38 places where the ball may land, all equally likely. A winning bet on a single number pays 35-to-1, meaning that the original stake is not lost, and 35 times that amount is won, so you receive 36 times what you've bet. Considering all 38 possible outcomes, the expected value of the profit resulting from a dollar bet on a single number is the sum of what you may lose times the odds of losing and what you will win times the odds of winning, that is,
The change in your financial holdings is −$1 when you lose, and $35 when you win. Thus one may expect, on average, to lose about five cents for every dollar bet, and the expected value of a one-dollar bet is $0.9474. In gambling, an event of which the expected value equals the stake (of which the bettor's expected profit is zero) is called a "fair game."
[edit] Mathematical definition
In general, if  is a random variable defined on a probability space
is a random variable defined on a probability space  , then the expected value of
, then the expected value of  , denoted
, denoted 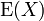 ,
,  ,
, 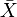 or
or 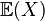 , is defined as
, is defined as
where the Lebesgue integral is employed. Note that not all random variables have an expected value, since the integral may not exist (e.g., Cauchy distribution). Two variables with the same probability distribution will have the same expected value, if it is defined.
If X is a discrete random variable with probability mass function p(x), then the expected value becomes
as in the gambling example mentioned above.
If the probability distribution of X admits a probability density function f(x), then the expected value can be computed as
It follows directly from the discrete case definition that if X is a constant random variable, i.e. X = b for some fixed real number b, then the expected value of X is also b.
The expected value of an arbitrary function of X, g(X), with respect to the probability density function f(x) is given by the inner product of f and g:
Using representations as Riemann–Stieltjes integral and integration by parts the formula can be restated as
if 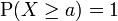 .
.
As a special case let α denote a positive real number, then
In particular, for α = 1, this reduces to:
if ![P[X \ge 0]=1](http://upload.wikimedia.org/math/8/4/8/8480e6201fb77890d87e12f903a2f77c.png) .
.
[edit] Conventional terminology
- When one speaks of the "expected price", "expected height", etc. one means the expected value of a random variable that is a price, a height, etc.
- When one speaks of the "expected number of attempts needed to get one successful attempt," one might conservatively approximate it as the reciprocal of the probability of success for such an attempt. Cf. expected value of the geometric distribution.
[edit] Properties
[edit] Constants
The expected value of a constant is equal to the constant itself; i.e., if 'c' is a constant, then 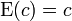 .
.
[edit] Monotonicity
If X and Y are random variables so that  almost surely, then
almost surely, then 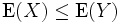 .
.
[edit] Linearity
The expected value operator (or expectation operator)  is linear in the sense that
is linear in the sense that
Note that the second result is valid even if X is not statistically independent of Y. Combining the results from previous three equations, we can see that
for any two random variables X and Y (which need to be defined on the same probability space) and any real numbers a and b.
[edit] Iterated expectation
[edit] Iterated expectation for discrete random variables
For any two discrete random variables X,Y one may define the conditional expectation:
which means that  is a function on y.
is a function on y.
Then the expectation of X satisfies
Hence, the following equation holds:
The right hand side of this equation is referred to as the iterated expectation and is also sometimes called the tower rule. This proposition is treated in law of total expectation.
[edit] Iterated expectation for continuous random variables
In the continuous case, the results are completely analogous. The definition of conditional expectation would use inequalities, density functions, and integrals to replace equalities, mass functions, and summations, respectively. However, the main result still holds:
[edit] Inequality
If a random variable X is always less than or equal to another random variable Y, the expectation of X is less than or equal to that of Y:
If  , then
, then 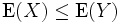 .
.
In particular, since 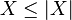 and
and  , the absolute value of expectation of a random variable is less than or equal to the expectation of its absolute value:
, the absolute value of expectation of a random variable is less than or equal to the expectation of its absolute value:
[edit] Non-multiplicativity
In general, the expected value operator is not multiplicative, i.e. 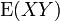 is not necessarily equal to
is not necessarily equal to 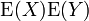 . If multiplicativity occurs, the X and Y variables are said to be uncorrelated (independent variables are a notable case of uncorrelated variables). The lack of multiplicativity gives rise to study of covariance and correlation.
. If multiplicativity occurs, the X and Y variables are said to be uncorrelated (independent variables are a notable case of uncorrelated variables). The lack of multiplicativity gives rise to study of covariance and correlation.
If one considers the joint PDF of X and Y, say j(X,Y), then the expectation of XY is
Now if X and Y are independent, then by definition j(X,Y)=f(X)g(Y) where f and g are the marginal PDFs for X and Y. Then
Observe that independence of X and Y is required only to write j(X,Y)=f(X)g(Y), and this is required to establish the third equality above.
[edit] Functional non-invariance
In general, the expectation operator and functions of random variables do not commute; that is
A notable inequality concerning this topic is Jensen's inequality, involving expected values of convex (or concave) functions.
[edit] The law of the unconscious statistician
[edit] Uses and applications of the expected value
The expected values of the powers of X are called the moments of X; the moments about the mean of X are expected values of powers of  . The moments of some random variables can be used to specify their distributions, via their moment generating functions.
. The moments of some random variables can be used to specify their distributions, via their moment generating functions.
To empirically estimate the expected value of a random variable, one repeatedly measures observations of the variable and computes the arithmetic mean of the results. If the expected value exists, this procedure estimates the true expected value in an unbiased manner and has the property of minimizing the sum of the squares of the residuals (the sum of the squared differences between the observations and the estimate). The law of large numbers demonstrates (under fairly mild conditions) that, as the size of the sample gets larger, the variance of this estimate gets smaller.
In classical mechanics, the center of mass is an analogous concept to expectation. For example, suppose X is a discrete random variable with values xi and corresponding probabilities pi. Now consider a weightless rod on which are placed weights, at locations xi along the rod and having masses pi (whose sum is one). The point at which the rod balances is  .
.
Expected values can also be used to compute the variance, by means of the computational formula for the variance
A very important application of the expectation value is in the field of quantum mechanics. The expectation value of a quantum mechanical operator 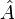 operating on a quantum state vector
operating on a quantum state vector  is written as
is written as 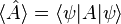 . The uncertainty in
. The uncertainty in 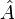 can be calculated using the formula
can be calculated using the formula 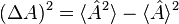 .
.
[edit] Expectation of matrices
If X is an 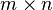 matrix, then the expected value of the matrix is defined as the matrix of expected values:
matrix, then the expected value of the matrix is defined as the matrix of expected values:
This is utilized in covariance matrices.
[edit] Computation
It is often useful to update a computed expected value as new data come in. This can be done as follows, where new_value is the count-th value, and we use the previous estimate 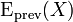 to compute
to compute  :
:
[edit] Formulas for special cases
[edit] Discrete distribution taking only non-negative integer values
When a random variable takes only values in {0,1,2,3,...} we can use the following formula for computing its expectation:
Proof:
interchanging the order of summation, we have
as claimed. This result can be a useful computational shortcut. For example, suppose we toss a coin where the probability of heads is p. How many tosses can we expect until the first heads? Let X be this number. Note that we are counting only the tails and not the heads which ends the experiment; in particular, we can have X = 0. The expectation of X may be computed by  . This is because the number of tosses is at least i exactly when the first i tosses yielded tails. This matches the expectation of a random variable with an Exponential distribution. We used the formula for Geometric progression:
. This is because the number of tosses is at least i exactly when the first i tosses yielded tails. This matches the expectation of a random variable with an Exponential distribution. We used the formula for Geometric progression: 
[edit] Continuous distribution taking non-negative values
Analogously with the discrete case above, when a continuous random variable X takes only non-negative values, we can use the following formula for computing its expectation:
Proof:
interchanging the order of integration, we have
as claimed.
[edit] See also
- Conditional expectation
- An inequality on location and scale parameters
- Expected value is also a key concept in economics, finance, and bioinformatics.
- The general term expectation
- Pascal's Wager
- Moment (mathematics)
- Expectation value (quantum mechanics)
- St. Petersburg Paradox
- Buffon's noodle
[edit] External links
|
|||||||||||||
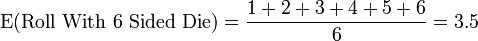



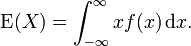

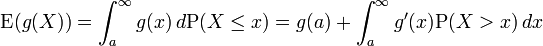


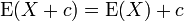



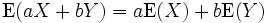
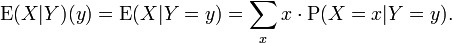
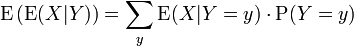
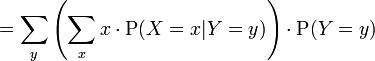

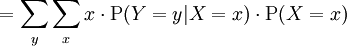




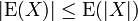

![E(XY)=\int_{X,Y}XYf(X)g(Y)\,dX\,dY=
\int_X\int_Y XYf(X)g(Y)\,dX\,dY=
\int_X Xf(X)\left[\int Yg(Y)\,dY\right]\,dX=\int_XXf(X)E(Y)\,dX=E(X)E(Y)](http://upload.wikimedia.org/math/c/7/0/c7022696e7c43c2b5727daeade24e583.png)