Mathematical coincidence
From Wikipedia, the free encyclopedia
| This article may require cleanup to meet Wikipedia's quality standards. Please improve this article if you can. (December 2007) |
| This article needs additional citations for verification. Please help improve this article by adding reliable references (ideally, using inline citations). Unsourced material may be challenged and removed. (June 2006) |
In mathematics, a mathematical coincidence can be said to occur when two expressions show a near-equality that lacks direct theoretical explanation.
Contents |
[edit] Introduction
A mathematical coincidence often comprises an integer, and the surprising (or "coincidental") feature is the fact that a real number is close to a small integer; or, more generally, to a rational number with a small denominator.
Given the large number of ways of combining mathematical expressions, one might expect a large number of coincidences to occur; this is one aspect of the strong law of small numbers. Although mathematical coincidences may be useful, they are mainly notable for their curiosity value.
[edit] Some examples
[edit] Rational approximants
Sometimes simple rational approximations are exceptionally close to interesting irrational values. These are explainable in terms of large terms in the continued fraction representation of the irrational value, but further insight into why such improbably large terms occur is often not available.
Rational approximants to the ratios of logs of numbers are often invoked as well, making coincidences between the powers of different numbers.
Many other coincidences are combinations of numbers that put them into the form that such rational approximants provide close relationships.
[edit] Concerning pi
- The first convergent of π, [3; 7] = 22/7 = 3.1428..., was known to Archimedes,[1] and is correct to about 0.04%. The third convergent of π, [3; 7, 15, 1] = 355/113 = 3.1415929..., found by Zu Chongzhi, is correct to six decimal places or about 85 parts in a billion; this high accuracy comes about because π has an unusually large next term in its continued fraction representation: π = [3; 7, 15, 1, 292, ...].
[edit] Concerning base 2
- The coincidence
 , correct to 2.4%, relates to the rational approximation
, correct to 2.4%, relates to the rational approximation  , or
, or  to within 0.3%. This relationship is used in engineering, for example to approximate a factor of two in power as 3 dB (actual is 3.0103 dB), or to relate a kilobyte to a kibibyte; see binary prefix.
to within 0.3%. This relationship is used in engineering, for example to approximate a factor of two in power as 3 dB (actual is 3.0103 dB), or to relate a kilobyte to a kibibyte; see binary prefix.
- Using 3/10 as the approximate value of log102, one finds the following approximations for logs of other ratios, starting from approximate integer relationships:
 leading to
leading to  (compare 0.4771, within 0.5%)
(compare 0.4771, within 0.5%) leading to
leading to  (compare 0.8451, within 0.6%)
(compare 0.8451, within 0.6%)
- Using 3/10 as the approximate value of log102, one finds the following approximations for logs of other ratios, starting from approximate integer relationships:
[edit] Concerning musical intervals
- The coincidence
 , from
, from  leads to the observation commonly used in music to relate the tuning of 7 semitones of equal temperament to a perfect fifth of just intonation:
leads to the observation commonly used in music to relate the tuning of 7 semitones of equal temperament to a perfect fifth of just intonation:  , correct to about 0.1%. The just fifth is the basis of Pythagorean tuning and most known systems of music. From the consequent approximation
, correct to about 0.1%. The just fifth is the basis of Pythagorean tuning and most known systems of music. From the consequent approximation 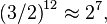 it follows that the circle of fifths terminates seven octaves higher than the origin.
it follows that the circle of fifths terminates seven octaves higher than the origin.
[edit] Numeric expressions
[edit] Concerning powers of pi
 correct to about 1.3%. This coincidence was used in the design of slide rules, where the "folded" scales are folded on π rather than
correct to about 1.3%. This coincidence was used in the design of slide rules, where the "folded" scales are folded on π rather than  because it is a more useful number and has the effect of folding the scales in about the same place.
because it is a more useful number and has the effect of folding the scales in about the same place. correct to 0.0004% (note 2, 227, and 23 are Chen primes).
correct to 0.0004% (note 2, 227, and 23 are Chen primes). (to about 0.15%).
(to about 0.15%). or
or  accurate to 8 decimal places (due to Ramanujan: Quarterly Journal of Mathematics, XLV, 1914, pp350-372). Ramanujan states that this "curious approximation" to π was "obtained empirically" and has no connection with the theory developed in the remainder of the paper. This can be told humorously as: Take the number "1234", transpose the first two digits and the last two digits, so the number becomes "2143". Divide that number by "two-two" (22, so 2143/22 = 97.40909...). Take the two-squaredth root (4th root) of this number. The final outcome is remarkably close to π (within about one part in a billion).
accurate to 8 decimal places (due to Ramanujan: Quarterly Journal of Mathematics, XLV, 1914, pp350-372). Ramanujan states that this "curious approximation" to π was "obtained empirically" and has no connection with the theory developed in the remainder of the paper. This can be told humorously as: Take the number "1234", transpose the first two digits and the last two digits, so the number becomes "2143". Divide that number by "two-two" (22, so 2143/22 = 97.40909...). Take the two-squaredth root (4th root) of this number. The final outcome is remarkably close to π (within about one part in a billion). , within 0.0023%
, within 0.0023%
[edit] Concerning the constant e
 , within 0.016%.
, within 0.016%.
- For any integer n, the early decimal digits of n − e are composed of 2,7,1, and 8, the first digits of e
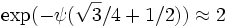 to 0.000015% (one part in ten million), where ψ is Polygamma function and exp is Exponential function.
to 0.000015% (one part in ten million), where ψ is Polygamma function and exp is Exponential function.
[edit] Containing both pi and e
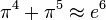 , within 0.000 005%
, within 0.000 005%
 is very close to 20 (Conway, Sloane, Plouffe, 1988); this is equivalent to
is very close to 20 (Conway, Sloane, Plouffe, 1988); this is equivalent to  [2]
[2]
[edit] Containing pi and e and phi (the Golden ratio)
 , within 0.3%.
, within 0.3%.
 , within 0.1%, both values having been claimed as the ratio of height to half-base of the Great Pyramid of Giza
, within 0.1%, both values having been claimed as the ratio of height to half-base of the Great Pyramid of Giza
[edit] Containing pi or e and number 163
- Ramanujan's constant:
 , within
, within  ,[3] it implies
,[3] it implies  , which is correct to about 20 digits.
, which is correct to about 20 digits.
Note:  is close to an integer for many values of n, most notably n = 163 is explained by algebraic number theory; see Heegner number.
is close to an integer for many values of n, most notably n = 163 is explained by algebraic number theory; see Heegner number.
[edit] Coincidences of units
- π seconds is a nanocentury (i.e., 10 - 7 years); correct to within about 0.5%
- one attoparsec per microfortnight approximately equals 1 inch per second (the actual figure is about 1.0043 inch per second).
- one furlong per fortnight is approximately equal to one centimetre per minute
- a cubic attoparsec (a cube where each edge is one attoparsec) is within 1% of a U.S. fluid ounce.
- one mile is about φ kilometers (correct to about 0.5%), where
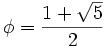 is the golden ratio. Since this is the limit of the ratio of successive terms of the Fibonacci sequence, this gives a sequence of approximations Fn mi = Fn + 1 km, e.g. 5 mi = 8 km, 8 mi = 13 km. Another good approximation is 1 mile = ln(5) km, 1 mile = 1.609344 km and ln(5) = 1.6094379124341...
is the golden ratio. Since this is the limit of the ratio of successive terms of the Fibonacci sequence, this gives a sequence of approximations Fn mi = Fn + 1 km, e.g. 5 mi = 8 km, 8 mi = 13 km. Another good approximation is 1 mile = ln(5) km, 1 mile = 1.609344 km and ln(5) = 1.6094379124341... - NA ≈ 279, where NA is Avogadro's number; correct to about 0.4%. This means that a yobibyte is slightly more than two moles of bytes. It also means that 1 mole of any material (e.g. 12 g carbon, or 25 l of gas at room temperature and normal pressure) cannot be halved more than 79 times.
- The speed of light in a vacuum is about one foot per nanosecond (accurate to 2%) or 3×108 m/s (accurate to about 0.07%) or 1 billion km/h (accurate to 7.93%)
[edit] Other numeric curiosities
 .
. , where φ is Golden ratio (an amusing equality with an angle expressed in degrees) (see Number of the Beast)
, where φ is Golden ratio (an amusing equality with an angle expressed in degrees) (see Number of the Beast) , where φ is Euler's totient function
, where φ is Euler's totient function and
and  are the only non-trivial (i.e. at least square) consecutive powers of positive integers (Catalan's conjecture). Likewise
are the only non-trivial (i.e. at least square) consecutive powers of positive integers (Catalan's conjecture). Likewise  and
and  are the only square and cube of positive integers that differ by 2.
are the only square and cube of positive integers that differ by 2. is the only integer solution of
is the only integer solution of  (see Lambert's W function for a formal solution method)
(see Lambert's W function for a formal solution method)
- Not only
 , but also
, but also  .
.  approximates the plastic constant to within 0.111%
approximates the plastic constant to within 0.111%- 31, 331, 3331 etc. up to 33333331 are all prime numbers, but then 333333331 is not. See also Formula for primes.
- The Fibonacci number F296182 is (probably) a semiprime, since F296182 = F148091 × L148091 where F148091 (30949 digits) and the Lucas number L148091 (30950 digits) are simultaneously probable primes.[4]
- In a discussion of the birthday problem, the number
 occurs which Arratia states is "amusingly" equal to ln(2) to 4 digits.[5]
occurs which Arratia states is "amusingly" equal to ln(2) to 4 digits.[5]
[edit] Decimal coincidences
 .
. .
. .
. ,
,  ,
,  ,
,  (Anomalous cancellation)
(Anomalous cancellation) and
and  .
.
 ;
; 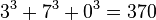 ;
;  ;
;  — all narcissistic numbers
— all narcissistic numbers- Along the same lines,
 and
and 
 .
.
 .
.


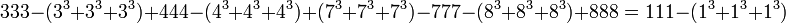
 and also
and also  when rounded to 8 digits is 0.05882353 mentioned by Gilbert Labelle in ~1980.
when rounded to 8 digits is 0.05882353 mentioned by Gilbert Labelle in ~1980.- The largest number which equals the sum of its digits in consecutive powers:
 . Other smaller examples include
. Other smaller examples include  , not to be confused with the narcissistic relation
, not to be confused with the narcissistic relation  mentioned above.
mentioned above.  is an example of three numbers which are very close to disproving Fermat's Last Theorem for n=12, the two sides differ by about 3x10 − 8%, the left hand side is in fact approximately equal to 1921.999999955912 (accurate to 10 decimal places).
is an example of three numbers which are very close to disproving Fermat's Last Theorem for n=12, the two sides differ by about 3x10 − 8%, the left hand side is in fact approximately equal to 1921.999999955912 (accurate to 10 decimal places).
[edit] See also
- For a list of coincidences in physics, see anthropic principle.
- Almost integer
- Birthday problem
- Narcissistic number
- The Strong Law of Small Numbers
[edit] References
- ^ Petr Beckmann (1993). A History of Pi. Barnes & Noble. ISBN 0880294183. http://books.google.com/books?id=XqqUUSyz138C&pg=PA170&dq=pi+%22continued+fractions%22+22-7&lr=&as_brr=3&ei=tkx1R7-ZKIiUtgOskqGeBw&sig=cmMFvVuWGZbBOeyUgeNSqhQAqQY#PPA170,M1.
- ^ a b "Almost Integer". Wolfram MathWorld. http://mathworld.wolfram.com/AlmostInteger.html.
- ^ Ramanujan, S. "Modular Equations and Approximations to pi." Quart. J. Pure Appl. Math. 45, 350-372, 1913-1914.
- ^ David Broadhurst, "Prime Curios!: 10660...49391 (61899-digits)" at The Prime Pages.
- ^ Arratia, Richard; and others (1990), "Poisson approximation and the Chen-Stein method", Statistical Science 5, (4,): 403–434
[edit] External links
- (Russian) В. Левшин. - Магистр рассеянных наук. - Москва, Детская Литература 1970, 256 с.
- Hardy, G. H. - A Mathematician's Apology. - New York: Cambridge University Press, 1993, (ISBN 0-521-42706-1)
- Sequence A032799 in the On-Line Encyclopedia of Integer Sequences
- Almost Integer from Wolfram MathWorld
- Various mathematical coincidences in the "Science & Math" section of futilitycloset.com
 ,
, 
 ,
,  ,
,  ,
, 
