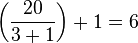Single transferable vote

From Wikipedia, the free encyclopedia

Jump to: navigation, search
 
This article is part of the
Politics series
Electoral methods
 
Single-winner
Multiple-winner
Random selection
Politics portal
v • d • e

The Single transferable vote (STV) is a system of preferential voting designed to minimize wasted votes and provide proportional representation while ensuring that votes are explicitly expressed for individual candidates rather than for party lists. It achieves this by using multi-seat constituencies (voting districts) and by transferring all votes that would otherwise be wasted to other eligible candidates. STV initially allocates an elector's vote to his or her most preferred candidate and then, after candidates have been either elected or eliminated, transfers surplus or unused votes according to the voter's stated preferences.

STV has had its widest adoption in the English-speaking world. As of 2007, STV is used for parliamentary elections in the Republic of Ireland (since 1919), Northern Irish Assembly and Malta. It is also used for the Australian Senate in the form of a group voting ticket, as well as certain regional and local elections in Australia, local government elections in the Republic of Ireland, local government elections in Scotland and some local government elections such as Dunedin and the capital city of Wellington in New Zealand — see History and use of the Single Transferable Vote. In the United States, it is used for city elections in Cambridge, Massachusetts, various student government elections, and will be used for certain city elections in Minneapolis, Minnesota, starting in 2009. A variation of STV known as BC-STV came within 2.4% of meeting the 60% threshold the government had set for adoption in British Columbia in a 2005 referendum, but it will be put to the voters a second time in May 2009. STV has been used for local elections in Scotland since May 2007.

STV was pioneered in Tasmania, Australia, where it has been in constant use in the Tasmanian House of Assembly since the early 1900s. It is known as Hare-Clark, in recognition of Thomas Hare, who initially developed the system and the Tasmanian Attorney General, Andrew Inglis Clark, who worked hard to have a modified version introduced. Hare-Clark has been subsequently modified to allow for improvements, such as rotating ballot papers (the Robson Rotation). It is held up by its supporters[who?] as being the best and fairest electoral system in the world, though political parties have often been resistant to adopting it[citation needed] because it requires candidates to compete publicly with one another, which is felt by some party members to damage party cohesion. Supporters feel that it is entirely appropriate that candidates make the case for their own election directly to the public.[citation needed]

Contents

[edit] Terminology

When STV is used for single-winner elections, it is equivalent to the non-proportional instant-runoff voting method. To differentiate them, STV used for multi-winner elections is sometimes called proportional representation through the single transferable vote, or PR-STV. The term STV usually refers to the multi-winner version, as it does in this article. In Australia STV is known as the Hare-Clark Proportional method, while in the United States it is sometimes called choice voting and preference voting.

[edit] Voting

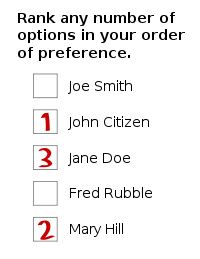
In STV, each voter ranks the list of candidates in order of preference. In other words (under the most common ballot design), they place a '1' beside their most preferred candidate, a '2' beside their second most preferred, and so on. The ballot paper submitted by the voter therefore contains an ordinal list of candidates. In the ballot paper shown in the image on the right, the preferences of the voter are as follows:

  1. John Citizen
  2. Mary Hill
  3. Jane Doe

[edit] Counting the votes

[edit] Setting the quota

In an STV election, a candidate requires a certain minimum number of votes – the quota (or threshold) – to be elected. A number of different quotas can be used; the most common is the Droop quota, given by the formula:

\left({{\rm votes} \over {\rm seats}+1}\right)+1

where:

  • Votes = the total number of valid (unspoilt) votes cast
  • Seats = the number of seats to be filled

The Droop quota finds the smallest number of votes that will fill the required number of seats and no more.

[edit] Finding the winners

An STV election proceeds according to the following steps:

  1. Any candidate who has reached or exceeded the required quota is declared elected.
  2. If not enough candidates have been elected, the count continues.
  3. If a candidate has more votes than the quota, then their surplus is transferred to other candidates according to the next preference on each voter's ballot.
  4. If no one meets the quota, the candidate with the fewest votes is eliminated and their votes are transferred.

This process repeats from step 1 until the required number of candidates have been elected.

Whether votes are transferred to elected candidates depends on the particular counting system chosen; systems that allow this subsequently redistribute the surplus, again.

A manual count is often halted when the number of seats to be filled equals the number of remaining candidates instead of counting votes until all candidates have reached a quota. Also, if the number of votes transferred is insufficient to either elect a candidate or change the order of candidates in the ranking, then multiple candidates may be excluded at once or a surplus may be held instead of being transferred. These procedures are common if ballots which do not list a full ranking of candidates become exhausted, because it is then possible for an insufficient number of candidates to reach the quota.

Because in STV, candidates who receive excess votes and candidates who are excluded have their votes transferred to other candidates, it is said to minimise wasted votes.

There are two basic forms of counting an STV election: one is based on the number of ballot papers allocated to a candidate; the other, more accurate system, is based on the value of the vote as it progresses throughout the count. This variance is important in the calculation of a candidate's surplus. The paper-based formula (the surplus divided by the number of ballot papers) undermines proportionality and the "one vote, same value" principle due to some votes increasing in value at the expense of other votes. The value-based formula (the value of the vote divided by the surplus) avoids these shortcomings, ensuring proportionality and maintaining the "one vote, same value" principle.

[edit] An example

Suppose a food election is conducted to determine what to serve at a party. There are 5 candidates, 3 of which will be chosen. The candidates are: Oranges, Pears, Chocolate, Strawberries, and Sweets. The 20 guests at the party have the preferences marked on their ballots in the two tables below (the first is a numerical representation, the second is pictorial). In the following table only some of the second preferences and none of the lower preferences are shown because they happen to not be needed in the count (a different set of votes could be constructed where first, second and third preferences of some voters must be considered).

# of Guests x x x x x x x x x x
x x x x		 x x x x x x
1st Preference Orange Pear Chocolate Chocolate Strawberry Candy
2nd Preference Orange Strawberry Candy

First, the quota is calculated. Using the Droop quota, with 20 voters and 3 winners to be found, the number of votes required to be elected is:

\left({20 \over {3+1}}\right) +1 = 6

When ballots are counted the election proceeds as follows:

Candidate: Orange Pear Chocolate Strawberry Candy
Round 1 x x x x x x x x x x
x x x x
x x x x		 x x Round 1: Chocolate is declared elected, since Chocolate has more votes than the quota
Round 2 x x x x x x x x x x
x x		 x x x x
x		 x x x Round 2: Chocolate's surplus votes transfer proportionately to Strawberry and Sweets according to the Chocolate voters' second choice preferences. However, even with the transfer of this surplus no candidate has reached the quota. Therefore Pear, who has the fewest votes, is eliminated.
Round 3 x x x x
x x		   x x x x
x x		 x x x x
x		 x x x Round 3: Pear's votes transfer to their second preference, Oranges, causing Orange to reach the quota and be elected. Orange barely meets the quota, and therefore has no surplus to transfer.
Round 4 x x x x
x x		   x x x x
x x		 x x x x
x		 x x x Round 4: Neither of the remaining candidates meets the quota, so Sweets are eliminated. Strawberry is the only remaining candidate and so wins the final seat.

Result: The winners are Chocolate, Oranges and Strawberries.

[edit] Differing counting methods

Main article: Counting Single Transferable Votes

STV systems differ in a number of ways, primarily in how they transfer votes as well as in the exact size of the quota used for determining winners. In fact, for this reason some have suggested that STV can be considered a family of voting systems rather than a single system. Today the Droop quota is the most commonly used quota. This ensures majority rule (except in rare cases) while maintaining the condition that no more candidates can reach a quota than there are seats to be filled. As originally conceived STV used the Hare quota, but this is now generally considered to be technically inferior. New Zealand uses a quota similar to the Droop quota — see: Electoral system of New Zealand.

The simplest methods of transferring surpluses under STV involve an element of randomness; partially random systems are used in the Republic of Ireland (except Senate elections) and Malta, among other places. For this reason the Gregory method (also known as Newland-Britain or Senatorial rules) was invented, which eliminates randomness by allowing for the transfer of fractions of votes. Gregory is in use in Northern Ireland, Republic of Ireland (Senate elections) and Australia. Both Gregory and these earlier methods have the problem, however, that in some circumstances they do not treat all votes equally. For this reason Meek's method and Warren's method have been invented.[1] However, while simpler methods can usually be counted by hand, except in a very small election Meek and Warren require counting to be conducted by computer. Meek is currently used in STV local body elections in New Zealand.

The most recent refinements of STV involve attempting to remove the problem of sequential exclusions. Sequential exclusions mean that sometimes STV eliminates, at an early stage in the count, a candidate who might have gone on to be elected later had they been allowed to remain in the contest. Systems such as CPO-STV, Schulze STV, and Sequential STV have been invented to overcome this problem by incorporating elements of Condorcet methods into STV. A method known as BTR-STV deals with the problem differently and more simply than these systems by simply making sure no such candidate could possibly be eliminated. None of these new methods has yet been used in a government election.

Most of the systems that are currently in use were designed to facilitate a manual counting process. With the ever increasing use of computer technology, many of the processes are in need of review. For example, in calculating a candidate's surplus, some systems use the number of ballot papers (surplus/number of papers) as opposed to the allocated value of the ballot papers to determine the value of any candidates surplus (value of the vote/surplus). Computers make it feasible to use the more accurate allocated value method, which maintains the one vote one value principle. A paper-based formula distorts the vote, increasing the value of some votes at the expense of others. An alternative to the method of segmentation and distribution of preferences from excluded candidates is to implement a reiterative counting system where the count is reset and started following every exclusion with votes redistributed according to the voter's nominated preference allocation.[2] [3] [4]

Manual counting issues, like segmentation transfers, need to be further considered in a computerised count. Segmentation transfers are where votes are distributed according to either the order in which they were received, last bundle or the grouping of common value of ballot papers to be transferred from highest to lowest. To simplify the counting process in a computerised count there should be single transaction per candidate without segmentation.

[edit] History and current use

Main article: History and use of the Single Transferable Vote
Carl Andræ

The concept of transferable voting was first proposed by Thomas Wright Hill in 1821. The system remained unused in real elections until 1855, when Carl Andræ proposed a transferable vote system for elections in Denmark. Andræ's system was used in 1856 to elect the Danish Rigsdag, and by 1866 it was also adapted for indirect elections to the second chamber, the Landsting, until 1915.

Thomas Hare

Although he was not the first to propose a system of transferable votes, the English barrister Thomas Hare is generally credited with the conception of STV, and he may have independently developed the idea in 1857. Hare's view was that STV should be a means of "making the exercise of the suffrage a step in the elevation of the individual character, whether it be found in the majority or the minority." In Hare's original STV system, he further proposed that electors should have the opportunity of discovering which candidate their vote had ultimately counted for, to improve their personal connection with voting.[5] This is unnecessary in modern STV elections, however, as an individual voter can discover how their vote was ultimately distributed by viewing detailed election results. This is particularly easy to do using Meek's method, where only the final weightings of each candidate need to be published.

The noted political essayist, John Stuart Mill, was a friend of Hare and an early proponent of STV, praising it in his essay Considerations on Representative Government.[6] His contemporary, Walter Bagehot, also praised the Hare system for allowing everyone to elect an MP, even ideological minorities, but also argued that the Hare system would create more problems than it solved: "[the Hare system] is inconsistent with the extrinsic independence as well as the inherent moderation of a Parliament - two of the conditions we have seen, are essential to the bare possibility of parliamentary government."[7]

Advocacy of STV spread through the British Empire, leading it to be sometimes known as British Proportional Representation. In 1896, Andrew Inglis Clark was successful in persuading the Tasmanian House of Assembly to be the first parliament in the world elected by what became known as the Hare-Clark system, named after himself and Thomas Hare.

Meek also considered a variant on his system which would have allowed for equal preferences to be expressed.

[edit] Issues

Main article: Issues affecting the Single Transferable Vote

A frequent concern with STV among electorates considering its adoption is its relative complexity compared with plurality voting methods.

STV differs from all other proportional-representation systems in actual use in that candidates of one party can be elected on transfers from voters for other parties. Hence, the use of STV may reduce the role of political parties in the electoral process and corresponding partisanship in the resulting government.

As a multi-member system, filling vacancies between elections can be problematic, and a variety of responses have been devised. The countback method is used in the Australian Capital Territory; Tasmania; Victoria; Malta; and Cambridge, Massachusetts. Casual vacancies are filled re-examining the ballot papers data from the previous election. Another option is to have a head official or remaining members of the elected body appoint a new member to fulfil the vacancy. A third alternative to fulfil a vacancy is to hold a single-winner by-election (effectively instant-runoff); this allows each party to choose a new candidate and all voters to participate. Another alternative is to have the candidates themselves create an ordered list of successors before leaving their seat. In the European Parliament, a departing Republic of Ireland or Northern Ireland member is replaced with the top eligible name from a replacement list submitted by the candidate at the time of the original election. This method is also used in the Northern Ireland Assembly.

Standing too few candidates may result in all of them being elected in the early stages, and votes being transferred to candidates of other parties. Standing too many candidates might result in first-preference votes being spread too thinly among them, and consequently several potential winners with broad second-preference appeal may be eliminated before others are elected and their second-preference votes distributed. In practice, most voters will preference candidates from the same party in order, which minimises the impact of this potential shortcoming of STV.

The outcome of voting under STV is proportional within a single election to the collective preference of voters, assuming voters have ranked their real preferences and vote along strict party lines. However, due to other voting mechanisms usually used in conjunction with STV, such as a district or constituency system, an election using STV may not guarantee proportionality across all districts put together.

STV systems in use in different countries vary, both in ballot design and in whether or not voters are obliged to provide a full list of preferences. In jurisdictions such as the Republic of Ireland and Northern Ireland, voters are permitted to rank as many or as few candidates as they wish. Consequently voters sometimes, for example, rank only the candidates of a single party, or of their most preferred parties. A minority of voters, especially if they do not fully understand the system, may even 'bullet vote', only expressing a first preference. Allowing voters to rank only as many candidates as they wish grants them greater freedom but can also lead to some voters ranking so few candidates that their vote eventually becomes 'exhausted'–that is, at a certain point during the count it can no longer be transferred and therefore loses an opportunity to influence the result.

STV provides proportionality by transferring votes to minimise waste, and therefore also minimises the number of unrepresented or disenfranchised voters.

According to the Gibbard-Satterthwaite theorem tactical voting is possible in all non-dictatorial deterministic voting systems. A number of methods of tactical or strategic voting exist that can be used in elections conducted using STV. In general these methods are only effective in marginal districts and only affect the allocation of a single seat per district.

Academic analysis of voting systems such as STV generally centers on the voting system criteria that they pass. No preference voting system satisfies all the criteria described in Arrow's impossibility theorem: in particular, STV fails to achieve independence of irrelevant alternatives (like most other vote-based ordering systems) as well as monotonicity.

[edit] See also

[edit] References

  1. ^ Hill, I.D. (1987). "Algorithm 123 — Single Transferable Vote by Meek’s method".
  2. ^ van der Craats, Anthony. "The Wright System - Submission for reform to the Australian Parliament Joint Standing Committee on Electoral Matters" (PDF). JSCEM. http://www.aph.gov.au/house/committee/em/elect07/subs/sub051.pdf. 
  3. ^ van der Craats, Anthony. "Rules and procedures for a Reiterative Proportional Representation Single Transferable Vote counting system" (PDF). JSCEM. http://www.aph.gov.au/house/committee/em/elect07/subs/sub051.1.pdf. 
  4. ^ van der Craats, Anthony. "One Vote One Value - Change that Counts" (PDF). JSCEM. http://www.aph.gov.au/house/committee/em/elect07/subs/sub051.2.pdf. 
  5. ^ Lambert & Lakeman (1955). "Voting in democracies". London : Faber, pg. 245.
  6. ^ Mill, J.S. "Considerations on Representative Government." Online at http://www.gutenberg.org/dirs/etext04/conrg10h.htm. Accessed 25 May 2007.
  7. ^ Bagehot, Walter. "English Constitution".

[edit] External links

[edit] Information and summaries

[edit] Simulations and software

[edit] Articles and publications

[edit] Proponent groups

Retrieved from "http://en.wikipedia.org/wiki/Single_transferable_vote"
Personal tools