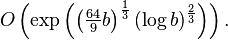Integer factorization

From Wikipedia, the free encyclopedia

Jump to: navigation, search
"Prime decomposition" redirects here. For the prime decomposition theorem for 3-manifolds, see Prime decomposition (3-manifold).

In number theory, integer factorization is the breaking down of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer.

When the numbers are very large, no efficient integer factorization algorithm is publicly known; a 2005 effort by F. Bahr, M. Boehm, J. Franke, T. Kleinjung factored a 193-digit number (RSA-640) utilizing 30 2.2GHz-Opteron-CPU years over a span of 5 months.[1] The presumed difficulty of this problem is at the heart of certain algorithms in cryptography such as RSA. Many areas of mathematics and computer science have been brought to bear on the problem, including elliptic curves, algebraic number theory, and quantum computing.

Not all numbers of a given length are equally hard to factor. The hardest instances of these problems (for currently known techniques) are semiprimes, the product of two prime numbers. When they are both large, randomly chosen, and about the same size (but not too close), even the fastest prime factorization algorithms on the fastest computers can take enough time to make the search impractical.

Contents

[edit] Prime decomposition

By the fundamental theorem of arithmetic, every positive integer greater than one has a unique prime factorization. However, the fundamental theorem of arithmetic gives no insight into how to obtain an integer's prime factorization; it only guarantees its existence.

Given an algorithm for integer factorization, one can factor any integer down to its constituent prime factors by repeated application of this algorithm.

[edit] Practical applications

The hardness of this problem, to use a term from computational complexity theory describing the difficulty of efficiently solving specific computational problems, lies at the heart of several important cryptographic systems. A fast integer factorization algorithm would mean that the RSA public-key algorithm is not secure. Some cryptographic systems, such as the Rabin public-key algorithm and the Blum Blum Shub pseudo-random number generator can make a stronger guarantee — any means of breaking them can be used to build a fast integer factorization algorithm; if integer factorization is hard, then they are strong. In contrast, it may turn out that there are attacks on the RSA problem more efficient than integer factorization, though none is currently published.

A similar hard problem with cryptographic applications is the discrete logarithm problem.

Even in the absence of cryptographic systems based on its hardness, integer factorization also has many positive applications in algorithms. For example, once an integer n is placed in its prime factorization representation, it enables the rapid computation of multiplicative functions on n. It can also be used to save storage, since any multiset of prime numbers can be stored without loss of information as its product; this was exploited, for example, by the Arecibo message.

[edit] Current state of the art

See also: integer factorization records

A team at the German Federal Agency for Information Technology Security (BSI) holds the record for factorization of semiprimes in the series proposed by the RSA Factoring Challenge sponsored by RSA Security. On May 9, 2005, this team announced factorization of RSA-200, a 663-bit number (200 decimal digits), using the general number field sieve.

The same team later announced factorization of RSA-640, a smaller number containing 193 decimal digits (640 bits), on November 4, 2005.

Both factorizations required several months of computer time using the combined power of 80 AMD Opteron CPUs.

[edit] Difficulty and complexity

If a large, b-bit number is the product of two primes that are roughly the same size, then no algorithm has been published that can factor in polynomial time, i.e., that can factor it in time O(bk) for some constant k. There are published algorithms that are faster than O((1+ε)b) for all positive ε, i.e., sub-exponential.

The best published asymptotic running time is for the general number field sieve (GNFS) algorithm, which, for a b-bit number n, is:

O\left(\exp\left(\left(\begin{matrix}\frac{64}{9}\end{matrix} b\right)^{1\over3} (\log b)^{2\over3}\right)\right).

For an ordinary computer, GNFS is the best published algorithm for large n (more than about 100 digits). For a quantum computer, however, Peter Shor discovered an algorithm in 1994 that solves it in polynomial time. This will have significant implications for cryptography if a large quantum computer is ever built. Shor's algorithm takes only O(b3) time and O(b) space on b-bit number inputs. In 2001, the first 7-qubit quantum computer became the first to run Shor's algorithm. It factored the number 15.

When discussing what complexity classes the integer factorization problem falls into, it's necessary to distinguish two slightly different versions of the problem:

  • The function problem version: given an integer N, find an integer d with 1 < d < N that divides N (or conclude that N is prime). This problem is trivially in FNP and it's not known whether it lies in FP or not. This is the version solved by most practical implementations.
  • The decision problem version: given an integer N and an integer M with 1 ≤ M ≤ N, does N have a factor d with 1 < d < M? This version is useful because most well-studied complexity classes are defined as classes of decision problems, not function problems. This is a natural decision version of the problem, analogous to those frequently used for optimization problems, because it can be combined with binary search to solve the function problem version in a logarithmic number of queries.

It is not known exactly which complexity classes contain the decision version of the integer factorization problem. It is known to be in both NP and co-NP. This is because both YES and NO answers can be trivially verified given the prime factors (we can verify their primality using the AKS primality test, and that their product is N by multiplication). In fact, providing we require the factors to be listed in order, the fundamental theorem of arithmetic will guarantee that there is only one possible string that will be accepted; this shows that the problem is in both UP and co-UP.[2] It is known to be in BQP because of Shor's algorithm. It is suspected to be outside of all three of the complexity classes P, NP-Complete, and co-NP-Complete. If it could be proved that it is in either NP-Complete or co-NP-Complete, that would imply NP = co-NP. That would be a very surprising result, and therefore integer factorization is widely suspected to be outside both of those classes. Many people have tried to find classical polynomial-time algorithms for it and failed, and therefore it is widely suspected to be outside P.

In contrast, the decision problem "is N a composite number?" (or equivalently: "is N a prime number?") appears to be much easier than the problem of actually finding the factors of N. Specifically, the former can be solved in polynomial time (in the number n of digits of N) with the AKS primality test. In addition, there are a number of probabilistic algorithms that can test primality very quickly in practice if one is willing to accept the small possibility of error. The ease of primality testing is a crucial part of the RSA algorithm, as it is necessary to find large prime numbers to start with.

[edit] Factoring algorithms

[edit] Special-purpose

A special-purpose factoring algorithm's running time depends on the properties of its unknown factors: size, special form, etc. Exactly what the running time depends on varies between algorithms. For example, trial division is considered special purpose because the running time is roughly proportional to the size of the smallest factor.

[edit] General-purpose

A general-purpose factoring algorithm's running time depends solely on the size of the integer to be factored. This is the type of algorithm used to factor RSA numbers. Most general-purpose factoring algorithms are based on the congruence of squares method.

[edit] Other notable algorithms

[edit] Notes

  1. ^ RSA-640 is factored!
  2. ^ Lance Fortnow. Computational Complexity Blog: Complexity Class of the Week: Factoring. September 13, 2002. http://weblog.fortnow.com/2002/09/complexity-class-of-week-factoring.html

[edit] References

  • Donald Knuth. The Art of Computer Programming, Volume 2: Seminumerical Algorithms, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89684-2. Section 4.5.4: Factoring into Primes, pp. 379–417.
  • Richard Crandall and Carl Pomerance (2001). Prime Numbers: A Computational Perspective (1st edition ed.). Springer. ISBN 0-387-94777-9.  Chapter 5: Exponential Factoring Algorithms, pp. 191–226. Chapter 6: Subexponential Factoring Algorithms, pp. 227–284. Section 7.4: Elliptic curve method, pp. 301–313.

[edit] External links

v • d • e
Number-theoretic algorithms
Primality tests
Sieving algorithms
Integer factorization algorithms
Other algorithms
Italics indicate that algorithm is for numbers of special forms; bold indicates deterministic algorithm for primality tests.
Retrieved from "http://en.wikipedia.org/wiki/Integer_factorization"
Personal tools