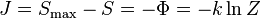Negentropy

From Wikipedia, the free encyclopedia

Jump to: navigation, search

The negentropy, also negative entropy or syntropy, of a living system is the entropy that it exports to keep its own entropy low; it lies at the intersection of entropy and life. The concept and phrase "negative entropy" were introduced by Erwin Schrödinger in his 1943 popular-science book What is life?[1] Later, Léon Brillouin shortened the phrase to negentropy,[2][3] to express it in a more "positive" way: a living system imports negentropy and stores it.[4] In 1974, Albert Szent-Györgyi proposed replacing the term negentropy with syntropy. That term may have originated in the 1940s with the Italian mathematician Luigi Fantappiè, who tried to construct a unified theory of biology and physics. (This attempt has not gained renown nor borne great fruit.) Buckminster Fuller tried to popularize this usage, but negentropy remains common.

In a note to What is Life? Schrödinger explained his use of this phrase.

“ [...] if I had been catering for them [physicists] alone I should have let the discussion turn on free energy instead. It is the more familiar notion in this context. But this highly technical term seemed linguistically too near to energy for making the average reader alive to the contrast between the two things. ”

Contents

[edit] Information theory

In information theory and statistics, negentropy is used as a measure of distance to normality.[5][6][7] Consider a signal with a certain distribution. If the signal is Gaussian, the signal is said to have a normal distribution. Negentropy is always nonnegative, is invariant by any linear invertible change of coordinates, and vanishes if and only if the signal is Gaussian.

Negentropy is defined as

J(p_x) = S(\phi_x) - S(p_x)\,

where S(φx) stands for the differential entropy of the Gaussian density with the same mean and variance as px and S(px) is the differential entropy of px:

S(p_x) = - \int p_x(u) \log p_x(u) du

Negentropy is used in statistics and signal processing. It is related to network entropy, which is used in Independent Component Analysis.[8][9] Negentropy can be understood intuitively as the information that can be saved when representing px in an efficient way; if px were a random variable (with Gaussian distribution) with the same mean and variance, would need the maximum length of data to be represented, even in the most efficient way. Since px is less random, then something about it is known beforehand, it contains less unknown information, and needs less length of data to be represented in an efficient way.

[edit] Correlation between statistical negentropy and Gibbs' free energy

Willard Gibbs’ 1873 available energy (free energy) graph, which shows a plane perpendicular to the axis of v (volume) and passing through point A, which represents the initial state of the body. MN is the section of the surface of dissipated energy. Qε and Qη are sections of the planes η = 0 and ε = 0, and therefore parallel to the axes of ε (internal energy) and η (entropy) respectively. AD and AE are the energy and entropy of the body in its initial state, AB and AC its available energy (Gibbs free energy) and its capacity for entropy (the amount by which the entropy of the body can be increased without changing the energy of the body or increasing its volume) respectively.

There is a physical quantity closely linked to free energy (free enthalpy), with a unit of entropy and isomorphic to negentropy known in statistics and information theory. In 1873 Willard Gibbs created a diagram illustrating the concept of free energy corresponding to free enthalpy. On the diagram one can see the quantity called capacity for entropy. The said quantity is the amount of entropy that may be increased without changing an internal energy or increasing its volume.[10] In other words, it is a difference between maximum possible, under assumed conditions, entropy and its actual entropy. It corresponds exactly to the definition of negentropy adopted in statistics and information theory. A similar physical quantity was introduced in 1869 by Massieu for the isothermal process [11][12][13] (both quantities differs just with a figure sign) and then Planck for the isothermal-isobaric process [14] More recently, the Massieu-Planck thermodynamic potential, known also as free entropy, has been shown to play a great role in the so-called entropic formulation of statistical mechanics, [15] applied among the others in molecular biology.[16] and thermodynamic non-equilibriumi processes. [17]


J = S_\max - S = -\Phi = -k \ln Z\,
where:
J - negentropy (Gibbs "capacity for entropy")
Φ – Massieu potential
Z - partition function
k - Boltzmann constant

[edit] Organization theory

In 1988, on the basis of Shannon's definition of statistical entropy, Mario Ludovico[18] gave a formal definition of syntropy, as a measurement of the degree of organization internal to any system formed by interacting components. According to that definition, syntropy is a quantity complementary to entropy. The sum of the two quantities defines a constant value, specific of the system of which that constant value identifies the transformation potential. By use of such definitions, the theory develops equations apt to describe/simulate any possible evolution of the system, either toward higher/lower levels of "internal organization" (i.e., syntropy) or toward the system's collapse.[19]

In risk management, negentropy is the force that seeks to achieve effective organizational behavior and lead to a steady predictable state.[20]

[edit] Notes

  1. ^ Schrödinger, Erwin What is Life - the Physical Aspect of the Living Cell, Cambridge University Press, 1944
  2. ^ Brillouin, Leon: (1953) "Negentropy Principle of Information", J. of Applied Physics, v. 24(9), pp. 1152-1163
  3. ^ Léon Brillouin, La science et la théorie de l'information, Masson, 1959
  4. ^ Mae-Wan Ho, What is (Schrödinger's) Negentropy?, Bioelectrodynamics Laboratory, Open university Walton Hall, Milton Keynes
  5. ^ Aapo Hyvärinen, Survey on Independent Component Analysis, node32: Negentropy, Helsinki University of Technology Laboratory of Computer and Information Science
  6. ^ Aapo Hyvärinen and Erkki Oja, Independent Component Analysis: A Tutorial, node14: Negentropy, Helsinki University of Technology Laboratory of Computer and Information Science
  7. ^ Ruye Wang, Independent Component Analysis, node4: Measures of Non-Gaussianity
  8. ^ P. Comon, Independent Component Analysis - a new concept?, Signal Processing, 36 287-314, 1994.
  9. ^ Didier G. Leibovici and Christian Beckmann, An introduction to Multiway Methods for Multi-Subject fMRI experiment, FMRIB Technical Report, Oxford Centre for Functional Magnetic Resonance Imaging of the Brain (FMRIB), Department of Clinical Neurology, University of Oxford, John Radcliffe Hospital, Headley Way, Headington, Oxford, UK.
  10. ^ Willard Gibbs, A Method of Geometrical Representation of the Thermodynamic Properties of Substances by Means of Surfaces, Transactions of the Connecticut Academy, 382-404 (1873)
  11. ^ Massieu, M. F. (1869a). Sur les fonctions caractéristiques des divers fluides. C. R. Acad. Sci. LXIX:858-862.
  12. ^ Massieu, M. F. (1869b). Addition au precedent memoire sur les fonctions caractéristiques. C. R. Acad. Sci. LXIX:1057-1061.
  13. ^ Massieu, M. F. (1869), Compt. Rend. 69 (858): 1057.
  14. ^ Planck, M. (1945). Treatise on Thermodynamics. Dover, New York.
  15. ^ Antoni Planes, Eduard Vives, Entropic Formulation of Statistical Mechanics, Entropic variables and Massieu-Planck functions 2000-10-24 Universitat de Barcelona
  16. ^ John A. Scheilman, Temperature, Stability, and the Hydrophobic Interaction, Biophysical Journal 73 (December 1997), 2960-2964, Institute of Molecular Biology, University of Oregon, Eugene, Oregon 97403 USA
  17. ^ Z. Hens and X. de Hemptinne, Non-equilibrium Thermodynamics approach to Transport Processes in Gas Mixtures, Department of Chemistry, Catholic University of Leuven, Celestijnenlaan 200 F, B-3001 Heverlee, Belgium
  18. ^ Mario Ludovico, L'evoluzione sintropica dei sistemi urbani - Elementi per una teoria dei sistemi auto-finalizzati (Syntropy in the Evolution of Urban Systems - Elements for a Theory of Self-Organized Systems), Bulzoni, Roma 1988-1991
  19. ^ Here is a summary of the syntropy theory.
  20. ^ Pedagogical Risk and Governmentality: Shantytowns in Argentina in the 21st Century (see p. 4).

[edit] See also

Retrieved from "http://en.wikipedia.org/wiki/Negentropy"
Personal tools