algorithm algorithms analysis collaboration collaborative collaborative-filtering collaborative_filtering collaborativefiltering development drupal filter filtering netflix network one programming rating recommendation recommendations research slope slopeone social software statistics stats tagging tools

My tags:

From Wikipedia, the free encyclopedia

Collaborative filtering is a technique used by recommender systems to combine different users' opinions and tastes in order to achieve personalized recommendations. There are at least two classes of collaborative filtering: user-based techniques are derived from similarity measures between users and item-based techniques compare the ratings given by different users. Slope One is a family of algorithms used for Collaborative filtering introduced in Slope One Predictors for Online Rating-Based Collaborative Filtering by Daniel Lemire and Anna Maclachlan. Arguably, it is the simplest form of non-trivial item-based collaborative filtering based on ratings. Their simplicity makes it especially easy to implement them efficiently while their accuracy is often on par with more complicated and computationally expensive algorithms.

Contents 1 Item-based collaborative filtering of rated resources and overfitting 2 Item-based collaborative filtering of purchase statistics 3 Slope one collaborative filtering for rated resources 4 Algorithmic Complexity of Slope One 5 Recommender Systems using Slope One 6 Open Source software implementing Slope One 7 Footnotes

[edit] Item-based collaborative filtering of rated resources and overfitting

When ratings of items are available, such as is the case when people are given the option of ratings resources (between 1 and 5, for example), collaborative filtering aims to predict the ratings of one individual based on his past ratings and on a (large) database of ratings contributed by other users.

Example. Can we predict the rating an individual would give to the new Celine Dion album given that he gave the Beatles 5 out of 5?

In this context, item-based Collaborative Filtering ^[1][2] predicts the ratings on one item based on the ratings on another item, typically using linear regression (f(x) = ax + b). Hence, if there are 1,000 items, there could be up to 1,000,000 linear regressions to be learned, and so, up to 2,000,000 regressors. This approach may suffer from severe overfitting^[3] unless we select only the pairs of items for which several users have rated both items.

A better alternative may be to learn a simpler predictor such as f(x) = x + b: experiments show that this simpler predictor (called Slope One) sometimes outperforms^[3] linear regression while having half the number of regressors. This simplified approach also reduces storage requirements and latency.

Item-based collaborative is just one form of collaborative filtering. Other alternatives include user-based collaborative filtering where relationships between users are of interest, instead. However, item-based collaborative filtering is especially scalable with respect to the number of users.

[edit] Item-based collaborative filtering of purchase statistics

We are not always given ratings: when the users provide only binary data (the item was purchased or not), then Slope One and other rating-based algorithm do not apply. Examples of binary item-based collaborative filtering include Amazon's item-to-item patented algorithm^[4] which computes the cosine between binary vectors representing the purchases in a user-item matrix.

Being arguably simpler than even Slope One, the Item-to-Item algorithm offers an interesting point of reference. Let us consider an example.

Sample purchase statistics

Customer	Item 1	Item 2	Item 3
John	Bought it	Didn't buy it	Bought it
Mark	Didn't buy it	Bought it	Bought it
Lucy	Didn't buy it	Bought it	Didn't buy it

In this case, the cosine between items 1 and 2 is:

,

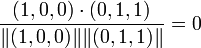The cosine between items 1 and 3 is:

,

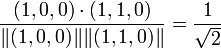Whereas the cosine between items 2 and 3 is:

.

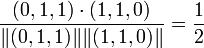Hence, a user visiting item 1 would receive item 3 as a recommendation, a user visiting item 2 would receive item 3 as a recommendation, and finally, a user visiting item 3 would receive item 1 (and then item 2) as a recommendation. The model uses a single parameter per pair of item (the cosine) to make the recommendation. Hence, if there are n items, up to n(n-1)/2 cosines need to be computed and stored.

[edit] Slope one collaborative filtering for rated resources

To drastically reduce overfitting, improve performance and ease implementation, the Slope One family of easily implemented Item-based Rating-Based Collaborative Filtering algorithms was proposed. Essentially, instead of using linear regression from one item's ratings to another item's ratings (f(x) = ax + b), it uses a simpler form of regression with a single free parameter (f(x) = x + b). The free parameter is then simply the average difference between the two items' ratings. It was shown to be much more accurate than linear regression in some instances^[3], and it takes half the storage or less.

Example:

1. Joe gave a 1 to Dion and an 1.5 to Lohan.
2. Jill gave a 2 to Dion.
3. How do you think Jill rated Lohan?
4. The Slope One answer is to say 2.5 (1.5-1+2=2.5).

For a more realistic example, consider the following table.

Sample rating database

Customer	Item 1	Item 2	Item 3
John	5	3	2
Mark	3	4	Didn't rate it
Lucy	Didn't rate it	2	5

In this case, the average difference in ratings between item 2 and 1 is (2+(-1))/2=0.5. Hence, on average, item 1 is rated above item 2 by 0.5. Similarly, the average difference between item 3 and 1 is 3. Hence, if we attempt to predict the rating of Lucy for item 1 using her rating for item 2, we get 2+0.5 = 2.5. Similarly, if we try to predict her rating for item 1 using her rating of item 3, we get 5+3=8.

If a user rated several items, the predictions are simply combined using a weighted average where a good choice for the weight is the number of users having rated both items. In the above example, we would predict the following rating for Lucy on item 1:

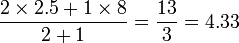
Hence, given n items, to implement Slope One, all that is needed is to compute and store the average differences and the number of common ratings for each of the n² pairs of items.

[edit] Algorithmic Complexity of Slope One

Suppose there are n items, m users, and N ratings. Computing the average rating differences for each pair of items requires up to n(n-1)/2 units of storage, and up to m n² time steps. This computational bound may be pessimistic: if we assume that users have rated up to y items, then it is possible to compute the differences in no more than n²+my². If a user has entered x ratings, predicting a single rating requires x time steps, and predicting all of his missing ratings requires up to (n-x)x time steps. Updating the database when a user has already entered x ratings, and enters a new one, requires x time steps.

It is possible to reduce storage requirements by partitionning the data (see Partition (database)) or by using sparse storage: pairs of items having no (or few) corating users can be omitted.

[edit] Recommender Systems using Slope One

• hitflip a DVD recommender system
• How Happy a general purpose review site
• inDiscover an MP3 recommender system
• RACOFI Composer a generic recommender system by the National Research Council
• Starfrosch an open MP3 blog community
• Value Investing News a stock market news site

[edit] Open Source software implementing Slope One

Python (programming language):

• A well documented Python implementation together with a tutorial

Java (programming language):

• Taste: a java-based collaborative library with support for Enterprise Java Beans (code sample)
• A standalone Java class implementing Slope One.
• The Cofi: A Java-Based Collaborative Filtering Library supports Slope One algorithms (documentation is so-so)

PHP:

• The Vogoo library supports Slope One algorithms (PHP)
• The Aspedia ECM API supports Slope One algorithms (PHP)
• There is PHP source code accompanying a technical report^[5] on Slope One algorithms
• A module for Drupal CMS that implements Slope One.
• The OpenSlopeOne supports Slope One algorithms, It's extremely fast, use pure php or mysql procedure (PHP)

Erlang (programming language):

• Philip Robinson implemented Slope One in Erlang.

Scala (programming language):

• Steve Jenson implemented Slope One in Scala.

Haskell (programming language):

• Bryan O'Sullivan implemented Slope One in Haskell.

Visual Basic for Applications:

• A Microsoft Excel spreadsheet Slope One implementation using VBA (requires enabled macros).

C Sharp (programming language):

• Kuber implemented Weighted Slope One in C#.

T-SQL:

• Charlie Zhu implemented Weighted Slope One in T-SQL.

[edit] Footnotes

1. ^ Slobodan Vucetic, Zoran Obradovic: Collaborative Filtering Using a Regression-Based Approach. Knowl. Inf. Syst. 7(1): 1-22 (2005)
2. ^ Badrul M. Sarwar, George Karypis, Joseph A. Konstan, John Riedl: Item-based collaborative filtering recommendation algorithms. WWW 2001: 285-295
3. ^ ^{a b c} Daniel Lemire, Anna Maclachlan, Slope One Predictors for Online Rating-Based Collaborative Filtering, In SIAM Data Mining (SDM'05), Newport Beach, California, April 21-23, 2005.
4. ^ Greg Linden, Brent Smith, Jeremy York, "Amazon.com Recommendations: Item-to-Item Collaborative Filtering," IEEE Internet Computing, vol. 07, no. 1, pp. 76-80, Jan/Feb, 2003
5. ^ Daniel Lemire, Sean McGrath, "Implementing a Rating-Based Item-to-Item Recommender System in PHP/SQL", Technical Report D-01, January 2005.