g-force
From Wikipedia, the free encyclopedia
The g-force of an object is its acceleration relative to free-fall. The unit of measure used is informally but commonly known as the "gee" (pronounced /ˈdʒiː/), symbolized as g (also G and g).[1] An acceleration of 1 g is generally considered as equal to standard gravity[2] (symbol: gn), which is defined as precisely 9.80665 metres per second squared.[3]
The g-force of an object is 0 g in any weightless environment such as free-fall or an orbiting satellite and is 1 g (upwards) for a stationary object on the Earth's surface. However, g-forces can be much greater than 1 g on, for instance, accelerating rockets, centrifuges, and rollercoasters.
The gee is not one of the International System of Units (SI). The SI unit of acceleration is m/s2.
Measurement of g-forces is typically achieved using a suitably calibrated accelerometer.
Contents |
[edit] Nature of the measure
Acceleration is a phenomenon familiar to anyone who has ridden in an automobile, as it is the rate at which speed or velocity changes with respect to some reference frame. Whenever a vehicle changes direction or speed, one feels lateral (side to side) and longitudinal (forward and backwards) forces. The value of one gee, 9.80665 meter per second per second, might be expressed in terms of m/s2 or in scientific literature as m s−2.
Acceleration and the gee can be expressed in more familiar terms: an acceleration of 1 g is a rate of change in velocity of approximately 35 km/h (22 mph) for each second that elapses. A high-performance automobile can brake (decelerate) at around 1 g. Accordingly, a high-performance automobile that is traveling at a speed of 35 km/h can brake at 1 g to a stop in one second. An automobile traveling at three times this speed, 66 mph, can brake to a stop in about three seconds. The expression “1 g = 9.80665 m s−2 ” means that for every second that elapses, velocity changes 9.80665 meters per second (≡35.30394 km/h). This rate of change in velocity can also be denoted as 9.80665 (meter per second) per second, or 9.80665 m/s2.
[edit] Gravitational and inertial acceleration
Accelerometers are often calibrated to measure g-force along one or more axes. If a stationary, single-axis accelerometer is oriented so that its measuring axis is horizontal, its output will be 0 g, and it will continue to be 0 g if mounted in an automobile traveling at a constant velocity on a level road. But if the car driver brakes sharply, the accelerometer will read about −0.9 g, corresponding to a backward acceleration. However, if the accelerometer is rotated by 90°, so that its axis points upwards, it will read +1 g upwards even though still stationary. In that situation, the accelerometer is subject to two forces: the gravitational force and the ground reaction force of the surface it is resting on. According to the theory of general relativity, only the latter force is a "real" force, due to an interaction between the accelerometer and the ground, and the reading is the acceleration the instrument would have if it were exclusively subject to that force. The gravitational force, instead, is considered a fictitious force, and it is explained by general relativity by stating that the Earth's large mass bends the spacetime, so that a stationary surface (an inertial frame of reference) in a downward gravitational field is equivalent to a surface accelerating upwards in absence of gravity. On the other hand, a surface with an acceleration exclusively due to the gravitational field (a free-falling surface) would be equivalent to a stationary surface in absence of gravity.
A three-axis accelerometer will output zero‑g on all three axes if it is dropped or otherwise put into a ballistic trajectory (also known as an inertial trajectory), so that it experiences "free fall," as do astonauts in orbit (astonauts experiences small tidal accelerations called microgravity, which are neglected for the sake of discussion here). Some notable amusement park rides can provide several seconds at near-zero g. Riding NASA’s “Vomit Comet” provides near-zero g for about 25 seconds at a time.
A single-axis accelerometer mounted in an airplane with its measurement axis oriented vertically reads +1 g when the plane is parked. When flying at a stable altitude (or at a constant rate of climb or descent), the accelerometer will continue to indicate 1 g. Under such conditions, the downward force acting upon the pilot’s body is the normal value of about 9.8 newtons per kilogram (N/kg) (one pound-force per pound). If the pilot pulls back on the stick until the accelerometer indicates 2 g, his weight (the force acting downwards on him) will double to 19.6 N/kg. A spring-based weighing scale, for the duration of a 2 g pitch-up maneuver, would reveal that his weight has truly doubled; a pilot who normally weighs 160 pounds would momentarily weigh 320 pounds.
[edit] Acceleration and forces
The expression, “g-force,” suggests that forces are involved whenever masses accelerate. Einstein, in his Theory of General Relativity, showed that gravity is actually a warpage of spacetime whereby even light—a massless beam of energy—follows a curved path when traveling past a massive body.
Whereas Einstein’s theory of gravitation is the most accurate one known, it is far from intuitive. Isaac Newton, 322 years ago, had a different view that, for most practical purposes, is an excellent scientific description of gravity and the laws of motion. Moreover, Newton’s descriptions of gravity and motion-related properties matches how humans commonly perceive them.
Newton gave the world his laws of motion in his 1687 scientific paper, Mathematical Principles of Natural Philosophy. In his second law of motion, the law of acceleration, Newton gave the world an equation that, when reduced to its simplest form, is written F = ma. The formula means that a force F acting on a body is equal to the mass m of the body times its acceleration a.
In Newton’s third law of motion, law of reciprocal actions, he wrote:
| “ | Law #3: All forces occur in pairs, and these two forces are equal in magnitude and opposite in direction. | ” |
To Newton (and for all practical purpose for the rest of us), his third law of motion means that not only does gravity behave as a force acting downwards on a rock held in your outstretched hand, but, simultaneously, your hand must generate an equal amount of force upwards for the rock to stay in one spot in your frame of reference. If you drop the rock, there are no longer equal forces acting upon the rock and it will accelerate downwards relative to you. This property is in accordance with Newton's first law of motion: the law of inertia. That law states that an object at rest tends to stay at rest and an object in motion tends to stay in motion with the same speed and in the same direction unless acted upon by unbalanced external forces.
In an airplane, the pilot’s seat can be thought of as a hand holding a rock; the pilot as the rock. When flying straight and level at 1 g, he is being acted upon by the force of gravity. His weight (a downward force) is 725 newtons, (163 pounds-force). Simultaneously, according to Newton’s third law, the law of reciprocal actions, the plane and the seat underneath the pilot provides an equal and opposite force acting against the force of gravity; the seat is pushing upwards with 725 newtons (163 pounds) of force. If the pilot were to suddenly pull back on the stick and make his plane accelerate upwards with respect to the earth at 9.8 m/s2, the total g‑force on his body is 2 g. His body is now generating a force of 1,450 newtons (326 pounds) downwards into his seat. According to Newton’s third law, this inertial acceleration is only possible because the seat is simultaneously pushing upwards with an equal force. Moreover, the relationship of acceleration, force, and mass is always in accordance with the teachings of his second law of motion: F = ma. The term “g‑force” reflects the fact that accelerating bodies entails forces.
When a swimmer stands on a diving board, the diving board bends because gravity is a force pushing down on everything, including the swimmer standing at the end of the flexible board. The ground pushes upwards with extra force once the diver climbs onto the diving tower. The product of the two opposing forces causes the board to bend. An accelerometer, a device for measuring g‑force, can be thought of as an indoor pool where the pool house represents the accelerometer’s housing; the diving board with the diver standing on it represents the sensing element inside. When an accelerometer is sitting stationary on a workbench with its measuring axis pointed upwards, it reads 1 g because of two forces: gravity pushing down on the entire accelerometer (including its internal contents), and the workbench pushing up on the accelerometer’s body. The only way to unload the sensing element inside (causing it to register 0 g) is to drop it and put it into a free‑fall. Since the external forces acting upon the accelerometer would then be unbalanced, it would accelerate downwards from your frame of reference.
Whether one is accelerating in a free‑fall, or are acting against gravitational acceleration by standing in one spot on the surface of the earth, or are inertially accelerating a body with respect to your frame of reference, all accelerations, or the lack thereof, are the product of Newtonian forces and how those forces are balanced.
[edit] Equation for g-force
If 
is an object's acceleration vector (in an inertial reference frame), and 
is the gravitational acceleration vector (so that the gravitational force on an object of mass m is 
), then the g-force of the object is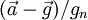 
.[2][4]
[edit] Units of measurement
The unit symbol for the gee is usually written as a lowercase roman (upright) g, which is the same symbol as for the gram. It may also be uppercase roman G or italic lowercase g.[1] These unit symbols should not be confused with the uppercase italic G, which denotes the gravitational constant, a physical constant that fundamentally relates mass and gravitational attraction.
[edit] Human tolerance
Human tolerances depend on the magnitude of the g-force, the length of time it is applied, the direction it acts, the location of application, and the posture of the body.[5][6]
The human body is flexible and deformable, particularly the softer tissues. A hard slap on the face may briefly impose hundreds of g locally but not produce any real damage; a constant 16 g for a minute, however, may be deadly. When vibration is experienced, relatively low peak g levels can be severely damaging if they are at the resonance frequency of organs and connective tissues.
To some degree, g-tolerance can be trainable, and there is also considerable variation in innate ability between individuals. In addition, some illnesses, particularly cardiovascular problems, reduce g-tolerance.
[edit] Vertical axis g-force
Aircraft, in particular, exert g-force along the axis aligned with the spine. This causes significant variation in blood pressure along the length of the subject's body, which limits the maximum g-forces that can be tolerated.
In aircraft, g-forces are often towards the feet, which forces blood away from the head; this causes problems with the eyes and brain in particular. As g-forces increase brownout/greyout can occur, where the vision loses hue. If g-force is increased further tunnel vision will appear, and then at still higher g, loss of vision, while consciousness is maintained. This is termed "blacking out". Beyond this point loss of consciousness will occur, sometimes known as "G-LOC" ("loc" stands for "loss of consciousness").[7] While tolerance varies, a typical person can handle about 5 g (49m/s²) before g-loc, but through the combination of special g-suits and efforts to strain muscles—both of which act to force blood back into the brain—modern pilots can typically handle 9 g (88 m/s²) sustained (for a period of time) or more (see High-G training).
Resistance to "negative" or upward g's, which drive blood to the head, is much lower. This limit is typically in the −2 to −3 g (−20 m/s² to −30 m/s²) range. The subject's vision turns red, referred to as a red out. This is probably because capillaries in the eyes swell or burst under the increased blood pressure.
[edit] Horizontal axis g-force
The human body is better at surviving g-forces that are perpendicular to the spine. In general when the acceleration is forwards, so that the g-force pushes the body backwards (colloquially known as "eyeballs in"[8]) a much higher tolerance is shown than when the acceleration is backwards, and the g-force is pushing the body forwards ("eyeballs out") since blood vessels in the retina appear more sensitive in the latter direction.
Early experiments showed that untrained humans were able to tolerate 17 g eyeballs-in (compared to 12 g eyeballs-out) for several minutes without loss of consciousness or apparent long-term harm.[9]
[edit] Rate of change of acceleration
The rate of change in acceleration is known as jerk (also jolt, surge, and lurch). Jerk is a concern, for instance, in the design of elevators, where a sudden lurching motion at the beginning and end of the ride would be uncomfortable for passengers.[10] Expressed in SI units, jerk is measured in m/s3. In non-SI units, jerk can be expressed simply as gees per second (g/s).
Jerk can be thought of as the rate at which an automobile driver applies force to the brake pedal. A high performance automobile can decelerate at 1 g. If the driver were to quickly “stomp” on the brake pedal with full force, the occupants will experience the full 1 g of deceleration in only a fraction of a second; a jerk of 5 g/s or greater. However, if the driver applies that same full force onto the brake pedal but applies it gradually over a period of two seconds, the abruptness is much more gentle, with a jerk of only 0.5 g/s.
[edit] Notable accelerations
| Value (or range) |
|
| The gyro rotors in Gravity Probe B and the free-floating proof masses in the TRIAD I navigation satellite[12] |
0 g |
| Moon surface at equator | 0.1654 g |
| Earth surface, sea level–standard | 1 g |
| Saturn V moon rocket just after launch | 1.14 g |
| Space Shuttle, maximum during launch and reentry | 3 g |
| High-g roller coasters[13] | 3.5–5 g |
| Formula One car, maximum under heavy braking | 5 g |
| Apollo 16 on reentry[14] | 7.19 g |
| Typical max. turn in an aerobatic plane or fighter jet | 9 g |
| Maximum for human on a rocket sled | 46.2 g |
| Sprint missile | 100 g |
| Brief human exposure survived in crash[15] | >100 g |
| Shock capability of mechanical wrist watches[16] |
5,000–7,500 g |
| Rating of electronics built into military artillery shells[17] | 15,500 g |
| 9 × 19 Parabellum handgun bullet (average along the length of the barrel)[18] |
31,000 g |
| 9 × 19 Parabellum handgun bullet, peak[19] | 190,000 g |
[edit] See also
- Cushioning
- Earth's gravity
- Gal (acceleration)
- Impact force
- Jerk (physics)
- Load factor
- Meter per second squared
- Shock (mechanics)
- Thrust-to-weight ratio
[edit] References
- ^ a b Symbol g: ESA: GOCE, Basic Measurement Units, NASA: Multiple G, Astronautix: Stapp, Honeywell: Accelerometers, Sensr LLC: GP1 Programmable Accelerometer, Farnell: accelometers, Delphi: Accident Data Recorder 3 (ADR3) MS0148, NASA: CONSTANTS AND EQUATIONS FOR CALCULATIONS, Jet Propulsion Laboratory: A Discussion of Various Measures of Altitude, Vehicle Safety Research Centre Loughborough: Use of smart technologies to collect and retain crash information, National Highway Traffic Safety Administration: Recording Automotive Crash Event Data
Symbol G: Lyndon B. Johnson Space Center: ENVIRONMENTAL FACTORS: BIOMEDICAL RESULTS OF APOLLO, Section II, Chapter 5, Honywell: Model JTF, General Purpose Accelerometer
Symbol g: MEMSIC: ACCELEROMETER PRIMER
- ^ a b ESA: GOCE, Basic Measurement Units
- ^ BIPM: Declaration on the unit of mass and on the definition of weight; conventional value of gn
- ^ Eshbach's Handbook of Engineering Fundamentals By Ovid W. Eshbach, pg 9
- ^ Balldin, Ulf I (2002). "33". Acceleration effects on fighter pilots. In: Medical conditions of Harsh Environments. 2. Washington, DC. http://www.bordeninstitute.army.mil/published_volumes/harshEnv2/harshEnv2.html. Retrieved on 2009-04-06.
- ^ Beyond the Black Box: the Forensics of Airplane Crashes; George Bibel, John Hopkins University Press, 2008 (ISBN 0-8018-8631-7), p350
- ^ Burton RR (January 1988). "G-induced loss of consciousness: definition, history, current status". Aviation, Space, and Environmental Medicine 59 (1): 2–5. PMID 3281645.
- ^ NASA Physiological Acceleration Systems
- ^ NASA Technical note D-337, Centrifuge Study of Pilot Tolerance to Acceleration and the Effects of Acceleration on Pilot Performance, by Brent Y. Creer, Captain Harald A. Smedal, USN (MC), and Rodney C. Vtlfngrove
- ^ US Patent 6,289,727
- ^ The Ejection Site: The Story of John Paul Stapp
- ^ Stanford University: Gravity Probe B, Payload & Spacecraft, and NASA: Investigation of Drag-Free Control Technology for Earth Science Constellation Missions. The TRIAD 1 satellite was a later, more advanced navigation satellite that was part of the U.S. Navy’s Transit, or NAVSAT system.
- ^ Beyond the Black Box: the Forensics of Airplane Crashes; George Bibel, John Hopkins University Press, 2008 (ISBN 0-8018-8631-7), p340
- ^ NASA: Table 2: Apollo Manned Space Flight Reentry G Levels
- ^ “Several Indy car drivers have withstood impacts in excess of 100 G without serious injuries.” Dennis F. Shanahan, M.D., M.P.H.: ”Human Tolerance and Crash Survivability, citing Society of Automotive Engineers. Indy racecar crash analysis. Automotive Engineering International, June 1999, 87-90. And National Highway Traffic Safety Administration: Recording Automotive Crash Event Data
- ^ Omega FAQ, Ball Watch Technology
- ^ "L-3 Communication's IEC Awarded Contract with Raytheon for Common Air Launched Navigation System". http://www.iechome.com/news/032003.htm.
- ^ Assuming a 124 grain (8.04 gram) bullet, a muzzle velocity of 1,150 ft/s (350 m/s), and a 4‑inch (102 mm) barrel.
- ^ Assuming a 124 grain (8.04 gram) bullet, a peak pressure of 35,000 psi (241 MPa) and 100 pounds (440 N) of friction.
