Coefficient of determination

From Wikipedia, the free encyclopedia

Jump to: navigation, search

In statistics, the coefficient of determination, R2 is used in the context of statistical models whose main purpose is the prediction of future outcomes on the basis of other related information. It is the proportion of variability in a data set that is accounted for by the statistical model. It provides a measure of how well future outcomes are likely to be predicted by the model.

There are several different definitions of R2 which are only sometimes equivalent. One class of such cases includes that of linear regression. In this case, R2 is simply the square of the sample correlation coefficient between the outcomes and their predicted values, or in the case of simple linear regression, between the outcome and the values being used for prediction. In such cases, the values vary from 0 to 1. Important cases where the computational definition of R2 can yield negative values, depending on the definition used, arise where the predictions which are being compared to the corresponding outcome have not derived from a model-fitting procedure using those data.

Contents

[edit] Definitions

A data set has values yi each of which has an associated modelled value fi. Here, the values yi are called the observed values and the modelled values fi are sometimes called the predicted values. The "variability" of the data set is measured through different sums of squares:

SS_{\rm tot}=\sum_i (y_i-\bar{y})^2, the total sum of squares (proportional to the sample variance);
SS_{\rm reg}=\sum_i ({f_i}-\bar{f})^2, the regression sum of squares, also called the explained sum of squares.
SS_{\rm err}=\sum_i (y_i - {f}_i)^2\,, the sum of squared errors, also called the residual sum of squares.

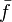In the above, \bar{y} and \bar{f} are the means of the observed data and modelled (predicted) values respectively.

Note: the notations SSR and SSE should be avoided, since in some texts their meaning is reversed to Explained sum of squares and Residual sum of squares.

The most general definition of the coefficient of determination is

R^2 \equiv 1 - {SS_{\rm err}\over SS_{\rm tot}}.\,

[edit] Relation to unexplained variance

In the general form, R2 can be seen to be related to the unexplained variance, since the second term compares the unexplained variance (variance of the model's errors) with the total variance (of the data). See fraction of variance unexplained.

[edit] As explained variance

In some cases the total sum of squares equals the sum of the two other sums of squares defined above,

SS_{\rm err}+SS_{\rm reg}=SS_{\rm tot}. \,

See sum of squares for a derivation of this result for one case where the relation holds. When this relation does hold, the above definition of R2 is equivalent to

R^{2} = {SS_{\rm reg} \over SS_{\rm tot} }.

In this form R2 is given directly in terms of the explained variance: it compares the explained variance (variance of the model's predictions) with the total variance (of the data).

This partition of the sum of squares holds for instance when the model values ƒi have been obtained by linear regression. A milder sufficient condition reads as follows: The model has the form

f_i=\alpha+\beta q_i \,

where the qi are arbitrary values that may or may not depend on i or on other free parameters (the common choice qi = xi is just one special case), and the coefficients α and β are obtained by minimizing the residual sum of squares.

This set of conditions is an important one and it has a number of implications for the properties of the fitted residuals and the modelled values. In particular, under these conditions:

\bar{f}=\bar{y}.\,

[edit] As squared correlation coefficient

Similarly, after least squares regression with a constant+linear model, R2 equals the square of the correlation coefficient between the observed and modelled (predicted) data values.

Under general conditions, an R2 value is sometimes calculated as the square of the correlation coefficient between the original and modelled data values. In this case, the value is not directly a measure of how good the modelled values are, but rather a measure of how good a predictor might be constructed from the modelled values (by creating a revised predictor of the form α + βƒi). According to Everitt (2002, p. 78), this usage is specifically the definition of the term "coefficient of determination": the square of the correlation between two (general) variables.

[edit] Interpretation

R2 is a statistic that will give some information about the goodness of fit of a model. In regression, the R2 coefficient of determination is a statistical measure of how well the regression line approximates the real data points. An R2 of 1.0 indicates that the regression line perfectly fits the data.

It is important to note that values of R2 outside the range 0 to 1 can occur where it is used to measure the agreement between observed and modelled values and where the "modelled" values are not obtained by linear regression and depending on which formulation of R2 is used. If the first formula above is used, values can never be greater than one. If the second expression is used, there are not constraints on the values obtainable.

In many (but not all) instances where R2 is used, the predictors are calculated by ordinary least-squares regression: that is, by minimising SSerr. In this case R-squared increases as we increase the number of variables in the model (R2 will not decrease). This illustrates a drawback to one possible use of R2, where one might try to include more variables in the model until "there is no more improvement". This leads to the alternative approach of looking at the adjusted R2. The explanation of this statistic is almost the same as R2 but it penalizes the statistic as extra variables are included in the model. For cases other than fitting by ordinary least squares, the R2 statistic can be calculated as above and may still be a useful measure. If fitting is by weighted least squares or generalized least squares, alternative versions of R2 can be calculated appropriate to those statistical frameworks, while the "raw" R2 may still be useful if it is more easily interpreted. Values for R2 can be calculated for any type of predictive model, which need not have a statistical basis.

[edit] In a linear model

Consider a linear model of the form

{Y_i = \beta_0 + \sum_j^p {\beta_j X_{i,j}} + \varepsilon_i},

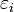where, for the ith case, Yi is the response variable, X_{i,1},\dots,X_{i,p} are p regressors, and \varepsilon_i is a mean zero error term. The quantities \beta_0,\dots,\beta_p are unknown coefficients, whose values are determined by least squares. The coefficient of determination R2 is a measure of the global fit of the model. Specifically, R2 is an element of [0, 1] and represents the proportion of variability in Yi that may be attributed to some linear combination of the regressors (explanatory variables) in X.

R2 is often interpreted as the proportion of response variation "explained" by the regressors in the model. Thus, R2 = 1 indicates that the fitted model explains all variability in y, while R2 = 0 indicates no 'linear' relationship between the response variable and regressors. An interior value such as R2 = 0.7 may be interpreted as follows: "Approximately seventy percent of the variation in the response variable can be explained by the explanatory variable. The remaining thirty percent can be explained by unknown, lurking variables or inherent variability."

A caution that applies to R2, as to other statistical descriptions of correlation and association is that "correlation does not imply causation." In other words, while correlations may provide valuable clues regarding causal relationships among variables, a high correlation between two variables does not represent adequate evidence that changing one variable has resulted, or may result, from changes of other variables.

In case of a single regressor, fitted by least squares, R2 is the square of the Pearson product-moment correlation coefficient relating the regressor and the response variable. More generally, R2 is the square of the correlation between the constructed predictor and the response variable.

[edit] Inflation of R2

In least squares regression, R2 is weakly increasing in the number of regressors in the model. As such, R2 alone cannot be used as a meaningful comparison of models with different numbers of independent variables. For a meaningful comparison between two models, an F-test can be performed on the residual sum of squares, similar to the F-tests in Granger causality. As a reminder of this, some authors denote R2 by R2p, where p is the number of columns in X

To demonstrate this property, first recall that the objective of least squares regression is:

\min_b SS_\text{err}(b) \Rightarrow \min_b \sum_i (y_i - X_ib)^2\,

The optimal value of the objective is weakly smaller as additional columns of X are added, by the fact that relatively unconstrained minimization leads to a solution which is weakly smaller than relatively constrained minimization. Given the previous conclusion and noting that SStot depends only on y, the non-decreasing property of R2 follows directly from the definition above.

[edit] Notes on interpreting R2

R2 does NOT tell whether:

  • the independent variables are a true cause of the changes in the dependent variable
  • omitted-variable bias exists
  • the correct regression was used
  • the most appropriate set of independent variables has been chosen
  • there is collinearity present in the data
  • the model might be improved by using transformed versions of the existing set of independent variables

[edit] Adjusted R2

Adjusted R2 (sometimes written as \bar R^2) is a modification of R2 that adjusts for the number of explanatory terms in a model. Unlike R2, the adjusted R2 increases only if the new term improves the model more than would be expected by chance. The adjusted R2 can be negative, and will always be less than or equal to R2. The adjusted R2 is defined as

{1-(1-R^{2}){n-1 \over n-p-1}} = {1-{SS_E \over SS_T}}{df_t \over df_e}

where p is the total number of regressors in the linear model (but not counting the constant term), and n is sample size.

The principle behind the Adjusted R2 statistic can be seen by rewriting the ordinary R2 as

{R^{2} = {1-{\textit{VAR}_E \over \textit{VAR}_T}}}

where VARE = SSE / n and VART = SST / n are estimates of the variances of the errors and of the observations, respectively. These estimates are replaced by notionally "unbiased" versions: VARE = SSE / (n − p − 1) and VART = SST / (n − 1).

Adjusted R2 does not have the same interpretation as R2. As such, care must be taken in interpreting and reporting this statistic. Adjusted R2 is particularly useful in the Feature selection stage of model building.

Adjusted R2 is not always better than R2: adjusted R2 will be more useful only if the R2 is calculated based on a sample, not the entire population. For example, if our unit of analysis is a state, and we have data for all counties, then adjusted R2 will not yield any more useful information than R2. The use of an adjusted R2 is an attempt to take account of the phenomenon of statistical shrinkage.[1]

[edit] Generalized R 2

Nagelkerke (1991) generalizes the definition of the coefficient of determination.

1. A generalized coefficient of determination should be consistent with the classical coefficient of determination when both can be computed.

2. Its value should also be maximised by the maximum likelihood estimation of a model.

3. It should be, at least asymptotically, independent of the sample size.

4. Its interpretation should be the proportion of the variation explained by the model.

5. It should be between 0 and 1, with 0 denoting that model does not explain any variation and 1 denoting that it perfectly explains the observed variation.

6. It should not have any unit.

The generalized R2 has all the preceding properties.

R^{2} = 1 - \left({L(0) \over L(\hat{\theta})}\right)^{2/n}

where L(0) is the likelihood of the model with only the intercept, {L(\hat{\theta})} is the likelihood of the estimated model and n is the sample size.

However, in the case of a logistic model, where L(\hat{\theta}) cannot be greater than 1, R2 is between 0 and R^{2}_\max = 1- (L(0))^{2/n} .

Thus, we define the maxed-rescaled R square = R^{2}/R^2_\max. [2]

[edit] See also

[edit] Notes

  1. ^ Everitt, B.S. (2002) The Cambridge Dictionary of Statistics, CUP. ISBN 0-521-81099-x (See entries for "Shrinkage", "Shrinkage formulae")
  2. ^ N. Nagelkerke, “A Note on a General Definition of the Coefficient of Determination,” Biometrika, vol. 78, no. 3, pp. 691-692, 1991.

[edit] References

  • Draper, N.R. and Smith, H. (1998). Applied Regression Analysis. Wiley-Interscience. ISBN 0-471-17082-8
  • Everitt, B.S. (2002). Cambridge Dictionary of Statistics (2nd Edition). CUP. ISBN 0-521-81099-x
  • Nagelkerke, Nico J.D. (1992) Maximum Likelihood Estimation of Functional Relationships, Pays-Bas, Lecture Notes in Statistics, Volume 69, 110p ISBN 0-387-97721-X.

[edit] External links

Retrieved from "http://en.wikipedia.org/wiki/Coefficient_of_determination"
Personal tools