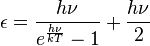Zero-point energy

From Wikipedia, the free encyclopedia

Jump to: navigation, search

In physics, the zero-point energy is the lowest possible energy that a quantum mechanical physical system may have and is the energy of the ground state. The quantum mechanical system that encapsulates this energy is the zero-point field. The concept was first proposed by Albert Einstein and Otto Stern in 1913. The term "zero-point energy" is a calque of the German Nullpunktenergie. All quantum mechanical systems have a zero point energy. The term arises commonly in reference to the ground state of the quantum harmonic oscillator and its null oscillations.

Zero-point energy is sometimes used as a synonym for the vacuum energy, an amount of energy associated with the vacuum of empty space. In cosmology, the vacuum energy is one possible explanation for the cosmological constant.[1] The variation in zero-point energy as the boundaries of a region of vacuum move leads to the Casimir effect, which is observable in nanoscale devices.

A related term is zero-point field, which is the lowest energy state of a field; i.e. its ground state, which is non-zero.[2]

Contents

[edit] History

In the year 1900, Max Planck derived the formula for the energy of a single "energy radiator", i.e. a vibrating atomic unit, as:

\epsilon = \frac{h\nu}{ e^{\frac{h\nu}{kT}}-1}

Here, h is Planck's constant, ν is the frequency, k is Boltzmann's constant, and T is the absolute temperature.

In the year 1913, using this formula as a basis, Albert Einstein and Otto Stern published a paper of great significance in which they suggested for the first time the existence of a residual energy that all oscillators have at absolute zero. They called this "residual energy" and then Nullpunktsenergie (in German), which later became translated as zero-point energy. They carried out an analysis of the specific heat of hydrogen gas at low temperature, and concluded that the data are best represented if the vibrational energy is taken to have the form:[3]

\epsilon = \frac{h\nu}{ e^{\frac{h\nu}{kT}}-1} + \frac{h\nu}{2}

According to this expression, an atomic system at absolute zero retains an energy of ½hν.

[edit] Foundational physics

The energy of a system is relative, and is defined only in relation to some given state (often called the reference state). One might associate a motionless system with zero energy, but doing so is purely arbitrary. In quantum physics, it is natural to associate the energy with the expectation value of a certain operator, the Hamiltonian of the system. For almost all quantum-mechanical systems, the lowest possible expectation value of this operator, which would be the zero-point energy, is not zero. Adding an arbitrary constant to the Hamiltonian gives an equivalent description of the physical system, but can make the zero-point energy different. Regardless of what constant is added to the Hamiltonian, the minimum momentum is always the same non-zero value.

[edit] Varieties of zero-point energy

The idea of zero-point energy occurs in a number of situations.

In ordinary quantum mechanics, the zero-point energy is the energy associated with the ground state of the system. The most famous such example is the energy 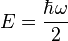E={\hbar\omega\over 2} associated with the ground state of the quantum harmonic oscillator. More precisely, the zero-point energy is the expectation value of the Hamiltonian of the system.

In quantum field theory, the fabric of space is visualized as consisting of fields, with the field at every point in space and time being a quantized simple harmonic oscillator, with neighboring oscillators interacting. In this case, one has a contribution of 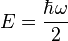E={\hbar\omega\over 2} from every point in space, resulting in a calculation of infinite zero-point energy. The zero-point energy is again the expectation value of the Hamiltonian; here, however, the phrase vacuum expectation value is more commonly used, and the energy is called the vacuum energy.

In quantum perturbation theory, it is sometimes said that the contribution of one-loop and multi-loop Feynman diagrams to elementary particle propagators are the contribution of vacuum fluctuations or the zero-point energy to the particle masses.

[edit] Experimental evidence for vacuum energy

A phenomenon that is commonly presented as evidence for the existence of zero-point energy in vacuum is the Casimir effect. This effect was proposed in 1948 by Dutch physicist Hendrik B. G. Casimir (Philips Research), who considered the quantized electromagnetic field between a pair of grounded, neutral metal plates. The vacuum energy contains contributions from all wavelengths, except those excluded by the spacing between plates. As the plates draw together, more wavelengths are excluded and the vacuum energy decreases. The decrease in energy means there must be a force doing work on the plates as they move. This force has been measured and found to be in good agreement with the theory. However, there is still some debate on whether vacuum energy explains the Casimir effect as the force can be explained equally well by a different theory involving charge-current interactions (the radiation-reaction picture), as argued by Robert Jaffe of MIT [4].

The experimentally measured lamb shift has been argued to be in part a zero-point energy effect.[5]

[edit] Gravitation and cosmology

Unsolved problems in physics: Why doesn't the zero-point energy of vacuum cause a large cosmological constant? What cancels it out?

In cosmology, the zero-point energy[6] offers an intriguing possibility for explaining the speculative positive values of the proposed cosmological constant. In brief, if the energy is "really there", then it should exert a gravitational force. In general relativity, mass and energy are equivalent; both produce a gravitational field. One obvious difficulty with this association is that the zero-point energy of the vacuum is absurdly large. Naively, it is infinite, but only differences in energy are physically measurable. The infinity can be removed by renormalization. In all practical calculations, this is how the infinity is handled. It is also arguable that new physics takes over at the Planck scale, and that the energy growth is cut off at that point.[7][8][9][10]

[edit] "Free energy" devices

As a scientific concept, the existence of zero point energy is not controversial although it may be debated. But perpetual motion machines and other power generating devices based on zero point energy are highly controversial. However, zero point energy devices wouldn't hypothetically operate in a closed system, thereby wouldn't qualify as perpetual motion machines. Descriptions of practical zero point energy devices have thus far lacked cogency. Experimental demonstrations of zero point energy devices have thus far lacked credibility. For reasons such as these, claims to zero point energy devices and great prospects for zero point energy are deemed pseudoscience.[11]

The discovery of zero point energy does not improve the world's prospects for perpetual motion machines. Much attention has been given to reputable science suggesting that zero point energy is infinite. But zero point energy is a minimum energy below which a thermodynamic system can never go, thus none of this energy can be withdrawn without altering the system to a different form in which the system has a lower zero point energy. The calculation that underlies the Casimir experiment, a calculation based on the formula predicting infinite vacuum energy, shows the zero point energy of a system consisting of a vacuum between two plates will decrease at a finite rate as the two plates are drawn together. The vacuum energies are predicted to be infinite, but the changes are predicted to be finite. Casimir combined the projected rate of change in zero point energy with the principle of conservation of energy to predict a force on the plates. The predicted force, which is very small and was experimentally measured to be within 5% of its predicted value, is finite.[12] Even though the zero point energy might be infinite, there is no theoretical basis or practical evidence to suggest that infinite amounts of zero point energy are available for use, that zero point energy can be withdrawn for free, or that zero point energy can be used in violation of conservation of energy.[13]

In principle, there remains the prospect of finding something that can be irreversibly altered or consumed to draw a net positive amount of energy through a zero point energy effect. Enthusiasm should be tempered by the realization that the Casimir effect produces tiny amounts of energy and those only in a non-renewable fashion.

[edit] References

  1. ^ http://users.physik.tu-muenchen.de/sfb375/Server/ringberg_2003/bauer.pdf
  2. ^ Gribbin, John (1998). Q is for Quantum - An Encyclopedia of Particle Physics. Touchstone Books. ISBN 0-684-86315-4. 
  3. ^ Laidler, Keith, J. (2001). The World of Physical Chemistry. Oxford University Press. ISBN 0198559194. 
  4. ^ Jaffe, R. L., Physical Review D. 72, 021301(R) (2005)
  5. ^ Margaret Hawton, Self-consistent frequencies of the electron-photon system, Phys. Rev. A 48, 1824 (1993) http://link.aps.org/doi/10.1103/PhysRevA.48.1824
  6. ^ http://www.setterfield.org/ZPE-Plasma_model.html
  7. ^ http://www.journaloftheoretics.com/Articles/2-5/dimario.pdf
  8. ^ http://digilander.libero.it/bubblegate/magneticanomaly.pdf
  9. ^ http://www.tewari.org/Theory_Papers/Tewari-Final%20Proof.pdf
  10. ^ http://arxiv.org/PS_cache/hep-ph/pdf/0112/0112078v1.pdf
  11. ^ U.S. Army National Ground Intelligence Center (NGIC) http://www.scribd.com/doc/297161/Zero-Point-Energy (excerpt) "Zero-Point Energy: Can We Get Something From Nothing"
  12. ^ http://math.ucr.edu/home/baez/physics/Quantum/casimir.html - The article refers to an "implied force" from the change in energy, which is the force required by conservation of energy.
  13. ^ http://www.sciam.com/article.cfm?id=follow-up-what-is-the-zer

[edit] Further reading

[edit] External links

Retrieved from "http://en.wikipedia.org/wiki/Zero-point_energy"
Personal tools