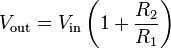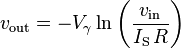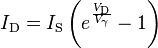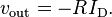Operational amplifier applications

From Wikipedia, the free encyclopedia

This article illustrates some typical applications of operational amplifiers. A simplified schematic notation is used, and the reader is reminded that many details such as device selection and power supply connections are not shown.

[edit] Caveats

It is important to note that the equations shown below, pertaining to each type of circuit, assume that an ideal op amp is used. Those interested in construction of any of these circuits for practical use should consult a more detailed reference. See the External links and Further reading sections.

[edit] Resistor choice

The resistors used in these configurations are typically in the kΩ range. Resistors less than 1 kΩ cause excessive current flow and possible damage to the device. Resistors greater than 1 MΩ cause excessive thermal noise and make the circuit operation susceptible to significant errors due to otherwise negligibly small bias or leakage currents. Resistors adjacent to gaps between metal contacts will combine with parasitic capacitances to change the frequency-dependent circuit behavior. In general, while resistor choice may seem arbitrary below, in a real implementation, the size and placement of resistors affects the influence of small unmodeled quantities on the output.

[edit] Nonzero input currents

An ideal operational amplifier draws no current from its inputs. Real operational amplifiers draw a small current from each of its inputs either due to biasing requirements or leakage. These (nominally DC) currents flow across the resistance networks connected to the inputs and produce small offset voltages at each input. If we assume that

the operational amplifier has an ideal CMRR,
the offset voltages are equal,

then the input currents will be negligible because the matched offset voltages will have no impact on the difference between the two inputs. So a good design will achieve matched input offset voltages. Note that many operational amplifiers that have MOSFET-based input stages have input leakage currents that will truly be negligible to most designs.

Assuming that the input currents into the operational amplifier are matched, the designer must ensure that the DC impedance looking out of each input are matched. To calculate the DC impedance looking out of each input,

Each voltage source, including the output of the operational amplifier, should be replaced with an electrical ground, and the resistance to ground should be calculated.

The impedance looking out of the non-inverting ( $+$ ) and inverting ( $-$ ) inputs must be matched in order to generate matching offset voltages that will be invisible to the operational amplifier.

Usually input currents are not matched. Most manufacturers provide a method for tuning the operational amplifier to balance the input currents (e.g., "offset null" or "balance" pins that can interact with an external voltage source attached to a potentiometer). Otherwise, a tunable external voltage can be added to one of the inputs in order to balance out the offset effect. In cases where a design calls for one input to be short-circuited to ground, that short circuit can be replaced with a variable resistance that can be tuned to mitigate the offset problem.

[edit] Power supply effects

Although the power supplies are not shown in the operational amplifier designs below, they can be critical in operational amplifier design. Not only can they introduce pernicious effects, but they also can be useful in designs (e.g., the extend the power capability of an operational amplifier to effectively building a second output stage that delivers additional current based on the current demanded by the operational amplifier).

Operational amplifiers have a specified PSRR that indicates how well the output can reject signals that appear on the power supply inputs. Power supply inputs are often noisy in large designs because the power supply is used by nearly every component in the design, and inductance effects prevent current from being instantaneously delivered to every component at once. As a consequence, when a component requires large injections of current (e.g., a digital component that is frequently switching from one state to another), nearby components can experience sagging at their connection to the power supply. This problem can be mitigated with copious use of bypass capacitors placed connected across each power supply pin and ground. When bursts of current are required by a component, the component can bypass the power supply by receiving the current directly from the nearby capacitor (which is then slowly charged by the power supply).

[edit] Linear circuit applications

[edit] Differential amplifier

Differential amplifier

Main article: Differential amplifier

The circuit shown is used for finding the difference of two voltages each multiplied by some constant (determined by the resistors).

The name "differential amplifier" should not be confused with the "differentiator", also shown on this page.

$V_{\text{out}} = \frac{ \left( R_{\text{f}} + R_1 \right) R_{\text{g}} }{\left( R_{\text{g}} + R_2 \right) R_1} V_2 - \frac{R_{\text{f}}}{R_1} V_1$

Differential $Z in$ (between the two input pins) = $R 1 + R 2$ (Note: this is approximate)

The "instrumentation amplifier", which is also shown on this page, is another form of differential amplifier that also provides high input impedance.

[edit] Amplified difference

Whenever $R 1 = R 2$ and $R f = R g$ ,

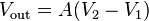$V_{\text{out}} = A (V_{\text{2}} - V_{\text{1}})\,$ and $A \triangleq \frac{ R_{\text{f}} }{ R_1 }$

[edit] Difference amplifier

When $R 1 = R f = R 2 = R g$ :

$V_\mathrm{out} = V_2 - V_1 \,\!$

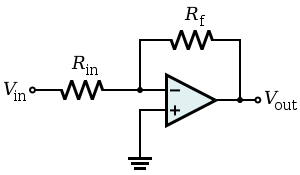
[edit] Inverting amplifier

Inverting amplifier

Uses negative feedback to invert and amplify a voltage (multiplies by a negative constant)

$V_{\text{out}} = -\frac{R_{\text{f}}}{R_{\text{in}}} V_{\text{in}}\!\$

$Z in = R in$ (because $V -$ is a virtual ground)
A third resistor, of value $R_{\text{f}} \| R_{\text{in}} \triangleq R_{\text{f}} R_{\text{in}} / (R_{\text{f}} + R_{\text{in}})$ , added between the non-inverting input and ground, while not necessary, minimizes errors due to input bias currents.

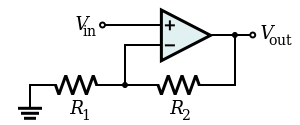
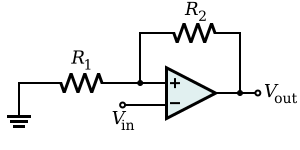
[edit] Non-inverting amplifier

Non-inverting amplifier

Amplifies a voltage (multiplies by a constant greater than 1)

$V_{\text{out}} = V_{\text{in}} \left( 1 + \frac{R_2}{R_1} \right)\,$

Input impedance
- The input impedance is at least the impedance between non-inverting ( $+$ ) and inverting ( $-$ ) inputs, which is typically 1 MΩ to 10 TΩ, plus the impedance of the path from the inverting ( $-$ ) input to ground (i.e., $R 1$ in parallel with $R 2$ ).
- Because negative feedback ensures that the non-inverting and inverting inputs match, the input impedance is actually much higher.
Although this circuit has a large input impedance, it suffers from error of input bias current.
- The non-inverting ( $+$ ) and inverting ( $-$ ) inputs draw small leakage currents into the operational amplifier.
- These input currents generate voltages that act like unmodeled input offsets. These unmodeled effects can lead to noise on the output (e.g., offsets or drift).
- Assuming that the two leaking currents are matched, their effect can be mitigated by ensuring the DC impedance looking out of each input is the same.
  - The voltage produced by each bias current is equal to the product of the bias current with the equivalent DC impedance looking out of each input. Making those impedances equal makes the offset voltage at each input equal, and so the non-zero bias currents will have no impact on the difference between the two inputs.
  - A resistor of value
    
    $R_1 \| R_2 \triangleq \left(\frac{1}{R_1} + \frac{1}{R_2}\right)^{-1} = \frac{ R_1 R_2 }{ R_1 + R_2 },\,$
  which is the equivalent resistance of $R 1$ in parallel with $R 2$ , between the $V in$ source and the non-inverting ( $+$ ) input will ensure the impedances looking out of each input will be matched.
  - The matched bias currents will then generate matched offset voltages, and their effect will be hidden to the operational amplifier (which acts on the difference between its inputs) so long as the CMRR is good.
- Very often, the input currents are not matched.
  - Most operational amplifiers provide some method of balancing the two input currents (e.g., by way of an external potentiometer).
  - Alternatively, an external offset can be added to the operational amplifier input to nullify the effect.
  - Another solution is to insert a variable resistor between the $V in$ source and the non-inverting ( $+$ ) input. The resistance can be tuned until the offset voltages at each input are matched.
  - Operational amplifiers with MOSFET-based input stages have input currents that are so small that they often can be neglected.

[edit] Voltage follower

Voltage follower

Used as a buffer amplifier, to eliminate loading effects or to interface impedances (connecting a device with a high source impedance to a device with a low input impedance). Due to the strong feedback, this circuit tends to get unstable when driving a high capacity load. This can be avoided by connecting the load through a resistor.

$V_{\text{out}} = V_{\text{in}} \!\$

$Z_{\text{in}} = \infin$ (realistically, the differential input impedance of the op-amp itself, 1 MΩ to 1 TΩ)

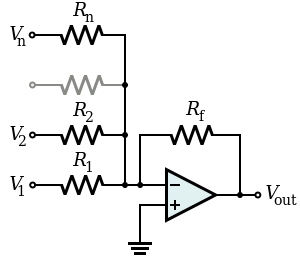
[edit] Summing amplifier

Summing amplifier

A summing amplifer sums several (weighted) voltages:

$V_{\text{out}} = -R_{\text{f}} \left( \frac{V_1}{R_1} + \frac{V_2}{R_2} + \cdots + \frac{V_n}{R_n} \right)$

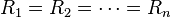When $R_1 = R_2 = \cdots = R_n$ , and $R f$ independent

$V_{\text{out}} = -\frac{R_{\text{f}}}{R_1} ( V_1 + V_2 + \cdots + V_n ) \!\$

When $R_1 = R_2 = \cdots = R_n = R_{\text{f}}$

$V_{\text{out}} = -( V_1 + V_2 + \cdots + V_n ) \!\$

Output is inverted
Input impedance of the nth input is $Z n = R n$ ( $V -$ is a virtual ground)

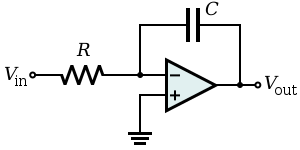
[edit] Integrator

Integrating amplifier

Integrates the (inverted) signal over time

$V_{\text{out}} = -\int_0^t \frac{ V_{\text{in}} }{RC} \, \operatorname{d}t + V_{\text{initial}}\,$

(where $V in$ and $V out$ are functions of time, $V initial$ is the output voltage of the integrator at time t = 0.)

Note that this can also be viewed as a low-pass electronic filter. It is a filter with a single pole at DC (i.e., where $ω = 0$ ) and gain.
There are several potential problems with this circuit.
- It is usually assumed that the input $V in$ has zero DC component (i.e., has a zero average value). Otherwise, unless the capacitor is periodically discharged, the output will drift outside of the operational amplifier's operating range.
- Even when $V in$ has no offset, the leakage or bias currents into the operational amplifier inputs can add an unexpected offset voltage to $V in$ that causes the output to drift. Balancing input currents and replacing the non-inverting ( $+$ ) short-circuit to ground with a resistor with resistance $R$ can reduce the severity of this problem.
- Because this circuit provides no DC feedback (i.e., the capacitor appears like an open circuit to signals with $ω = 0$ ), the offset of the output may not agree with expectations (i.e., $V initial$ may be out of the designer's control with the present circuit).

Many of these problems can be made less severe by adding a large resistor

R F

in parallel with the feedback capacitor. At significantly high frequencies, this resistor will have negligible effect. However, at low frequencies where there are drift and offset problems, the resistor provides the necessary feedback to hold the output steady at the correct value. In effect, this resistor reduces the DC gain of the "integrator" – it goes from infinite to some finite value

R F / R

.

[edit] Differentiator

Differentiating amplifier

Differentiates the (inverted) signal over time.

The name "differentiator" should not be confused with the "differential amplifier," which is also shown on this page. The former takes a derivative and the latter takes a difference (i.e., does subtraction).

$V_{\text{out}} = -RC \,\frac{\operatorname{d}V_{\text{in}} }{ \operatorname{d}t} \, \qquad \text{where } V_{\text{in}}\text{ and } V_{\text{out}} \text{ are functions of time.}$

Note that this can also be viewed as a high-pass electronic filter. It is a filter with a single zero at DC (i.e., where $ω = 0$ ) and gain.

[edit] Comparator

Comparator

Main article: Comparator

Compares two voltages and switches its output to indicate which voltage is larger.

$V_{\text{out}} = \left\{\begin{matrix} V_{\text{S+}} & V_1 > V_2 \\ V_{\text{S-}} & V_1 < V_2 \end{matrix}\right.$

(where $V s$ is the supply voltage and the opamp is powered by $+ V s$ and $- V s$ .)

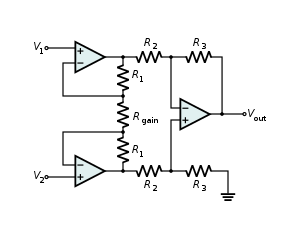
[edit] Instrumentation amplifier

Instrumentation amplifier

Main article: Instrumentation amplifier

Combines very high input impedance, high common-mode rejection, low DC offset, and other properties used in making very accurate, low-noise measurements

Is made by adding a non-inverting buffer to each input of the differential amplifier to increase the input impedance.

[edit] Schmitt trigger

Main article: Schmitt trigger

A bistable multivibrator implemented as a comparator with hysteresis.

Schmitt trigger with non-inverting hysteretic switching characteristic

In this configuration, the hysteresis curve is non-inverting (i.e., very negative inputs correspond to a negative output and very positive inputs correspond to a positive output), and the switching thresholds are 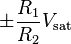$\pm \frac{R_1}{R_2}V_{\text{sat}}$ where $V sat$ is the greatest output magnitude of the operational amplifier.

Schmitt trigger with inverting hysteretic switching characteristic

Alternatively, the input and the ground may be swapped. In this configuration, the hysteresis curve is inverting (i.e., very negative inputs correspond to a positive output and vice versa), and the switching thresholds are $\pm \frac{R_1}{R_1 + R_2} V_{\text{sat}}$ . Such a configuration is used in the relaxation oscillator shown below.

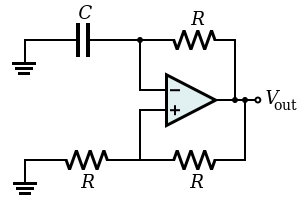
[edit] Relaxation oscillator

Main article: Relaxation oscillator

Relaxation oscillator implemented with inverting Schmitt trigger and RC network

By using an RC network to add slow negative feedback to the inverting Schmitt trigger, a relaxation oscillator is formed. The feedback through the RC network causes the Schmitt trigger output to oscillate in an endless symmetric square wave (i.e., the Schmitt trigger in this configuration is an astable multivibrator).

[edit] Inductance gyrator

Inductance gyrator

Main article: Gyrator

Simulates an inductor.

[edit] Zero level detector

Voltage divider reference

Zener sets reference voltage

[edit] Negative impedance converter (NIC)

Negative impedance converter

Main article: Negative impedance converter

Creates a resistor having a negative value for any signal generator

In this case, the ratio between the input voltage and the input current (thus the input resistance) is given by:

$R_{\text{in}} = -R_3 \frac{R_1}{R_2}$

In general, the components $R 1$ , $R 2$ , and $R 3$ need not be resistors; they can be any component that can be described with an impedance.

[edit] Non-linear configurations

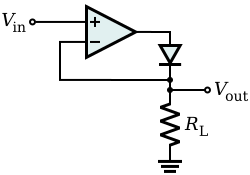
[edit] Precision rectifier

Precision rectifier

Main article: Precision rectifier

Although there are some limitations, this super diode circuit behaves like an ideal diode for the load $R L$ .

[edit] Logarithmic output

Logarithmic configuration

The relationship between the input voltage $v in$ and the output voltage $v out$ is given by:

$v_{\text{out}} = -V_{\gamma} \ln \left( \frac{v_{\text{in}}}{I_{\text{S}} \, R} \right)$

where

I S

is the saturation current.

If the operational amplifier is considered ideal, the negative pin is virtually grounded, so the current flowing into the resistor from the source (and thus through the diode to the output, since the op-amp inputs draw no current) is:

$\frac{v_{\text{in}}}{R} = I_{\text{R}} = I_{\text{D}}$

where

I D

is the current through the diode. As known, the relationship between the current and the voltage for a diode is:

$I_{\text{D}} = I_{\text{S}} \left( e^{\frac{V_{\text{D}}}{V_{\gamma}}} - 1 \right).$

This, when the voltage is greater than zero, can be approximated by:

$I_{\text{D}} \simeq I_{\text{S}} e^{\frac{V_{\text{D}}}{V_{\gamma}}}.$

Putting these two formulae together and considering that the output voltage is the negative of the voltage across the diode (

V out = - V D

), the relationship is proven.

Note that this implementation does not consider temperature stability and other non-ideal effects.

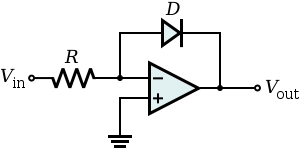
[edit] Exponential output

Exponential configuration

The relationship between the input voltage $v in$ and the output voltage $v out$ is given by:

$v_{\text{out}} = -R I_{\text{S}} e^{\frac{v_{\text{in}}}{V_{\gamma}}}$

where $I S$ is the saturation current.

Considering the operational amplifier ideal, then the negative pin is virtually grounded, so the current through the diode is given by:

$I_{\text{D}} = I_{\text{S}} \left( e^{\frac{V_{\text{D}}}{V_{\gamma}}} - 1 \right)$

when the voltage is greater than zero, it can be approximated by:

$I_{\text{D}} \simeq I_{\text{S}} e^{\frac{V_{\text{D}}}{V_{\gamma}}}.$

The output voltage is given by:

$v_{\text{out}} = -R I_{\text{D}}.\,$

[edit] Other applications

audio and video pre-amplifiers and buffers
voltage comparators
differential amplifiers
differentiators and integrators
filters
precision rectifiers
voltage regulator and current regulator
analog-to-digital converter
digital-to-analog converter
voltage clamps
oscillators and waveform generators
Schmitt trigger
Gyrator
Comparator
Active filter
Analog computer

[edit] See also

Operational amplifier
Current-feedback operational amplifier
Operational transconductance amplifier
Frequency compensation
George A. Philbrick
Voltage compensation reveals the philosophy behind op-amp inverting circuits with negative feedback.

[edit] References

[edit] Further reading

Paul Horowitz and Winfield Hill, The Art of Electronics. 2^nd ed. Cambridge University Press, Cambridge, 1989 ISBN 0-521-37095-7
Sergio Franco, Design with Operational Amplifiers and Analog Integrated Circuits, 3^rd ed., McGraw-Hill, New York, 2002 ISBN 0-07-232084-2

[edit] External links

The Wikibook Electronics has a page on the topic of

Op-Amps

Introduction to op-amp circuit stages, second order filters, single op-amp bandpass filters, and a simple intercom
Op Amps for EveryonePDF (1.96 MiB)
Hyperphysics – descriptions of common applications
Single supply op-amp circuit collectionPDF (163 KiB)
Op-amp circuit collectionPDF (962 KiB)
A Collection of Amp ApplicationsPDF (1.06 MiB) – Analog Devices Application note
Basic OpAmp ApplicationsPDF (173 KiB)
Handbook of operational amplifier applicationsPDF (2.00 MiB) – Texas Instruments Application note
Low Side Current Sensing Using Operational Amplifiers
Logarithmic amplifier
Precision half-wave rectifier
Precision full-wave rectifier
Log/anti-log generators, cube generator, multiply/divide ampPDF (165 KiB)
Logarithmically variable gain from a linear variable component
ECE 209: Operational amplifier basics – Brief document explaining zero error by naive high-gain negative feedback. Gives single OpAmp example that generalizes typical configurations.
ECE 327: Practical Integrators and Operational Amplifier Offset – Discusses sources of and ways of fixing offset and drift problems.
ECE 327: Voltage Regulators Procedures and Explanations – In the "Improving dynamic performance" section, discusses methods of using bypass capacitors to improve PSRR of components in designs.
Impedance and admittance transformations using operational amplifiers by D. H. Sheingold